Derivado direccional - Directional derivative

En matemáticas , la derivada direccional de una función diferenciable (escalar) multivariante a lo largo de un vector dado v en un punto dado x representa intuitivamente la tasa instantánea de cambio de la función, moviéndose a través de x con una velocidad especificada por v .

La derivada direccional de una función escalar f con respecto a un vector v en un punto (p. Ej., Posición) x puede denotarse mediante cualquiera de los siguientes:

{\ Displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = f '_ {\ mathbf {v}} (\ mathbf {x}) = D _ {\ mathbf {v}} f (\ mathbf {x}) = Df (\ mathbf {x}) (\ mathbf {v}) = \ partial _ {\ mathbf {v}} f (\ mathbf {x}) = \ mathbf {v} \ cdot {\ nabla f (\ mathbf {x})} = \ mathbf {v} \ cdot {\ frac {\ parcial f (\ mathbf {x})} {\ parcial \ mathbf {x}}}}

.

Por lo tanto, generaliza la noción de derivada parcial , en la que la tasa de cambio se toma a lo largo de una de las curvas de coordenadas curvilíneas , siendo todas las demás coordenadas constantes. La derivada direccional es un caso especial de la derivada Gateaux .

Definición

Un gráfico de contorno de , que muestra el vector de degradado en negro y el vector unitario escalado por la derivada direccional en la dirección de en naranja. El vector de gradiente es más largo porque el gradiente apunta en la dirección de mayor tasa de aumento de una función.

{\ Displaystyle f (x, y) = x ^ {2} + y ^ {2}}

{\ Displaystyle \ mathbf {u}}

{\ Displaystyle \ mathbf {u}}

La derivada direccional de una función escalar

{\ Displaystyle f (\ mathbf {x}) = f (x_ {1}, x_ {2}, \ ldots, x_ {n})}

a lo largo de un vector

{\ Displaystyle \ mathbf {v} = (v_ {1}, \ ldots, v_ {n})}

es la función definida por el límite ${\ Displaystyle \ nabla _ {\ mathbf {v}} {f}}$

{\ Displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = \ lim _ {h \ to 0} {\ frac {f (\ mathbf {x} + h \ mathbf {v }) -f (\ mathbf {x})} {h}}.}

Esta definición es válida en una amplia gama de contextos, por ejemplo, donde la norma de un vector (y por lo tanto un vector unitario) no está definida.

Para funciones diferenciables

Si la función f es derivable en x , entonces la derivada direccional existe a lo largo de cualquier vector v , y uno tiene

{\ Displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = \ nabla f (\ mathbf {x}) \ cdot \ mathbf {v}}

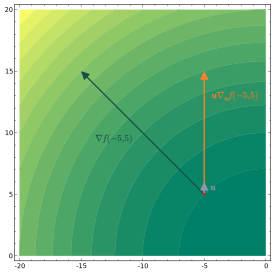
donde a la derecha denota el gradiente y es el producto escalar . Esto se deriva de definir una ruta y usar la definición de la derivada como un límite que se puede calcular a lo largo de esta ruta para obtener: ${\ Displaystyle \ nabla}$ ${\ Displaystyle \ cdot}$ ${\ Displaystyle h (t) = x + tv}$

{\ Displaystyle {\ begin {alineado} 0 & = \ lim _ {t \ to 0} {\ frac {f (x + tv) -f (x) -tDf (x) (v)} {t}} \\ & = \ lim _ {t \ to 0} {\ frac {f (x + tv) -f (x)} {t}} - Df (x) (v) = \ nabla _ {v} f (x) -Df (x) (v) \\\ flecha derecha & \ nabla f (\ mathbf {x}) \ cdot \ mathbf {v} = Df (x) (v) = \ nabla _ {\ mathbf {v}} { f} (\ mathbf {x}) \ end {alineado}}}

Intuitivamente, la derivada direccional de f en un punto x representa la tasa de cambio de f , en la dirección de v con respecto al tiempo, cuando se pasa de x .

Usando solo la dirección del vector

El ángulo α entre la tangente A y la horizontal será máximo si el plano de corte contiene la dirección del gradiente A .

En un espacio euclidiano , algunos autores definen la derivada direccional con respecto a un vector v arbitrario distinto de cero después de la normalización , por lo que es independiente de su magnitud y depende solo de su dirección.

Esta definición da la tasa de aumento de f por unidad de distancia recorrida en la dirección dada por v . En este caso, uno tiene

{\ Displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = \ lim _ {h \ to 0} {\ frac {f (\ mathbf {x} + h \ mathbf {v }) -f (\ mathbf {x})} {h | \ mathbf {v} |}},}

o en caso de que f sea diferenciable en x ,

{\ Displaystyle \ nabla _ {\ mathbf {v}} {f} (\ mathbf {x}) = \ nabla f (\ mathbf {x}) \ cdot {\ frac {\ mathbf {v}} {| \ mathbf {v} |}}.}

Restricción a un vector unitario

En el contexto de una función en un espacio euclidiano , algunos textos restringen el vector v a ser un vector unitario . Con esta restricción, ambas definiciones anteriores son equivalentes.

Propiedades

Muchas de las propiedades familiares de la derivada ordinaria son válidas para la derivada direccional. Estos incluyen, para cualquier función f y g definida en una vecindad de, y diferenciable en, p :

regla de suma :
${\ Displaystyle \ nabla _ {\ mathbf {v}} (f + g) = \ nabla _ {\ mathbf {v}} f + \ nabla _ {\ mathbf {v}} g.}$
regla del factor constante : para cualquier constante c ,
${\ Displaystyle \ nabla _ {\ mathbf {v}} (cf) = c \ nabla _ {\ mathbf {v}} f.}$
regla del producto (o regla de Leibniz ):
${\ Displaystyle \ nabla _ {\ mathbf {v}} (fg) = g \ nabla _ {\ mathbf {v}} f + f \ nabla _ {\ mathbf {v}} g.}$
regla de la cadena : si g es diferenciable en p y h es diferenciable en g ( p ), entonces
${\ Displaystyle \ nabla _ {\ mathbf {v}} (h \ circ g) (\ mathbf {p}) = h '(g (\ mathbf {p})) \ nabla _ {\ mathbf {v}} g (\ mathbf {p}).}$

En geometría diferencial

Deje que $M$ sea un diferenciable colector y $p$ un punto de $M$ . Suponga que $f$ es una función definida en una vecindad de $p$ , y diferenciable en $p$ . Si $v$ es un vector tangente a $M$ en $p$ , entonces la derivada direccional de $f a lo$ largo de $v$ , denotada de diversas formas como $df (v)$ (ver Derivada exterior ), (ver Derivada covariante ), (ver Derivada de Lie ), o (ver Espacio tangente § Definición mediante derivaciones ), se puede definir de la siguiente manera. Let $γ$ $: [-1, 1] \to$ $M$ ser una curva diferenciable con $γ$ $(0) =$ $p$ y $γ$ $'(0) =$ $v$ . Entonces la derivada direccional se define por ${\ Displaystyle \ nabla _ {\ mathbf {v}} f (\ mathbf {p})}$ ${\ Displaystyle L _ {\ mathbf {v}} f (\ mathbf {p})}$ ${\ Displaystyle {\ mathbf {v}} _ {\ mathbf {p}} (f)}$

{\ Displaystyle \ nabla _ {\ mathbf {v}} f (\ mathbf {p}) = \ left. {\ frac {d} {d \ tau}} f \ circ \ gamma (\ tau) \ right | _ {\ tau = 0}.}

Esta definición puede probarse independientemente de la elección de $γ$ , siempre que $γ$ se seleccione de la manera prescrita de modo que $γ' (0) = v$ .

La derivada de la mentira

La derivada de Lie de un campo vectorial a lo largo de un campo vectorial viene dada por la diferencia de dos derivadas direccionales (con torsión que desaparece): ${\ Displaystyle W ^ {\ mu} (x)}$ ${\ Displaystyle V ^ {\ mu} (x)}$

{\ Displaystyle {\ mathcal {L}} _ {V} W ^ {\ mu} = (V \ cdot \ nabla) W ^ {\ mu} - (W \ cdot \ nabla) V ^ {\ mu}.}

En particular, para un campo escalar , la derivada de Lie se reduce a la derivada direccional estándar: ${\ Displaystyle \ phi (x)}$

{\ Displaystyle {\ mathcal {L}} _ {V} \ phi = (V \ cdot \ nabla) \ phi.}

El tensor de Riemann

Las derivadas direccionales se utilizan a menudo en las derivaciones introductorias del tensor de curvatura de Riemann . Considere un rectángulo curvo con un vector infinitesimal δ a lo largo de un borde y δ ′ a lo largo del otro. Traducimos un covector S a lo largo de δ, luego δ ′ y luego restamos la traslación a lo largo de δ ′ y luego δ . En lugar de construir la derivada direccional usando derivadas parciales, usamos la derivada covariante . El operador de traducción para δ es entonces

{\ Displaystyle 1+ \ sum _ {\ nu} \ delta ^ {\ nu} D _ {\ nu} = 1 + \ delta \ cdot D,}

y para δ ′,

{\ Displaystyle 1+ \ sum _ {\ mu} \ delta '^ {\ mu} D _ {\ mu} = 1 + \ delta' \ cdot D.}

La diferencia entre los dos caminos es entonces

{\ Displaystyle (1+ \ delta '\ cdot D) (1+ \ delta \ cdot D) S ^ {\ rho} - (1+ \ delta \ cdot D) (1+ \ delta' \ cdot D) S ^ {\ rho} = \ sum _ {\ mu, \ nu} \ delta '^ {\ mu} \ delta ^ {\ nu} [D _ {\ mu}, D _ {\ nu}] S _ {\ rho}.}

Se puede argumentar que la no conmutatividad de las derivadas covariantes mide la curvatura de la variedad:

{\ Displaystyle [D _ {\ mu}, D _ {\ nu}] S _ {\ rho} = \ pm \ sum _ {\ sigma} R ^ {\ sigma} {} _ {\ rho \ mu \ nu} S_ { \ sigma},}

donde R es el tensor de curvatura de Riemann y el signo depende de la convención de signos del autor.

En teoría de grupos

Traducciones

En el álgebra de Poincaré , podemos definir un operador de traslación infinitesimal P como

{\ Displaystyle \ mathbf {P} = i \ nabla.}

(la i asegura que P es un operador autoadjunto ) Para un desplazamiento finito λ , la representación unitaria del espacio de Hilbert para traslaciones es

{\ Displaystyle U ({\ boldsymbol {\ lambda}}) = \ exp \ left (-i {\ boldsymbol {\ lambda}} \ cdot \ mathbf {P} \ right).}

Al usar la definición anterior del operador de traducción infinitesimal, vemos que el operador de traducción finito es una derivada direccional exponenciada:

{\ displaystyle U ({\ boldsymbol {\ lambda}}) = \ exp \ left ({\ boldsymbol {\ lambda}} \ cdot \ nabla \ right).}

Este es un operador de traducción en el sentido de que actúa sobre funciones multivariables f ( x ) como

{\ Displaystyle U ({\ boldsymbol {\ lambda}}) f (\ mathbf {x}) = \ exp \ left ({\ boldsymbol {\ lambda}} \ cdot \ nabla \ right) f (\ mathbf {x} ) = f (\ mathbf {x} + {\ boldsymbol {\ lambda}}).}

Prueba de la última ecuación -

En el cálculo estándar de una sola variable, la derivada de una función suave f ( x ) se define por (para ε pequeño )

{\ displaystyle {\ frac {df} {dx}} = {\ frac {f (x + \ varepsilon) -f (x)} {\ varepsilon}}.}

Esto se puede reorganizar para encontrar f ( x + ε ):

{\ Displaystyle f (x + \ varepsilon) = f (x) + \ varepsilon \, {\ frac {df} {dx}} = \ left (1+ \ varepsilon \, {\ frac {d} {dx}} \ derecha) f (x).}

De ello se deduce que es un operador de traducción. Esto se generaliza instantáneamente a funciones multivariables f ( x ) ${\ Displaystyle [1+ \ varepsilon \, (d / dx)]}$

{\ displaystyle f (\ mathbf {x} + {\ boldsymbol {\ varepsilon}}) = \ left (1 + {\ boldsymbol {\ varepsilon}} \ cdot \ nabla \ right) f (\ mathbf {x}). }

Aquí está la derivada direccional a lo largo del desplazamiento infinitesimal ε . Hemos encontrado la versión infinitesimal del operador de traducción: ${\ Displaystyle {\ boldsymbol {\ varepsilon}} \ cdot \ nabla}$

{\ displaystyle U ({\ boldsymbol {\ varepsilon}}) = 1 + {\ boldsymbol {\ varepsilon}} \ cdot \ nabla.}

Es evidente que la ley de multiplicación de grupos U ( g ) U ( f ) = U ( gf ) toma la forma

{\ Displaystyle U (\ mathbf {a}) U (\ mathbf {b}) = U (\ mathbf {a + b}).}

Entonces, suponga que tomamos el desplazamiento finito λ y lo dividimos en N partes ( N → ∞ está implícito en todas partes), de modo que λ / N = ε . En otras palabras,

{\ displaystyle {\ boldsymbol {\ lambda}} = N {\ boldsymbol {\ varepsilon}}.}

Luego, aplicando U ( ε ) N veces, podemos construir U ( λ ):

{\ displaystyle [U ({\ boldsymbol {\ varepsilon}})] ^ {N} = U (N {\ boldsymbol {\ varepsilon}}) = U ({\ boldsymbol {\ lambda}}).}

Ahora podemos conectar nuestra expresión anterior para U ( ε ):

{\ displaystyle [U ({\ boldsymbol {\ varepsilon}})] ^ {N} = \ left [1 + {\ boldsymbol {\ varepsilon}} \ cdot \ nabla \ right] ^ {N} = \ left [1 + {\ frac {{\ boldsymbol {\ lambda}} \ cdot \ nabla} {N}} \ right] ^ {N}.}

Usando la identidad

{\ Displaystyle \ exp (x) = \ left [1 + {\ frac {x} {N}} \ right] ^ {N},}

tenemos

{\ displaystyle U ({\ boldsymbol {\ lambda}}) = \ exp \ left ({\ boldsymbol {\ lambda}} \ cdot \ nabla \ right).}

Y como U ( ε ) f ( x ) = f ( x + ε ) tenemos

{\ displaystyle [U ({\ boldsymbol {\ varepsilon}})] ^ {N} f (\ mathbf {x}) = f (\ mathbf {x} + N {\ boldsymbol {\ varepsilon}}) = f ( \ mathbf {x} + {\ boldsymbol {\ lambda}}) = U ({\ boldsymbol {\ lambda}}) f (\ mathbf {x}) = \ exp \ left ({\ boldsymbol {\ lambda}} \ cdot \ nabla \ right) f (\ mathbf {x}),}

QED

Como nota técnica, este procedimiento solo es posible porque el grupo de traducción forma un subgrupo abeliano ( subálgebra de Cartan ) en el álgebra de Poincaré. En particular, la ley de multiplicación de grupos U ( a ) U ( b ) = U ( a + b ) no debe darse por sentada. También notamos que Poincaré es un grupo de Lie conectado. Es un grupo de transformaciones T ( ξ ) que se describen mediante un conjunto continuo de parámetros reales . La ley de multiplicación de grupos toma la forma ${\ Displaystyle \ xi ^ {a}}$

{\ Displaystyle T ({\ bar {\ xi}}) T (\ xi) = T (f ({\ bar {\ xi}}, \ xi)).}

Tomando como coordenadas de la identidad, debemos tener ${\ Displaystyle \ xi ^ {a} = 0}$

{\ Displaystyle f ^ {a} (\ xi, 0) = f ^ {a} (0, \ xi) = \ xi ^ {a}.}

Los operadores reales en el espacio de Hilbert están representados por operadores unitarios U ( T ( ξ )). En la notación anterior suprimimos la T ; ahora escribimos U ( λ ) como U ( P ( λ )). Para un pequeño vecindario alrededor de la identidad, la representación de la serie de poder

{\ Displaystyle U (T (\ xi)) = 1 + i \ sum _ {a} \ xi ^ {a} t_ {a} + {\ frac {1} {2}} \ sum _ {b, c} \ xi ^ {b} \ xi ^ {c} t_ {bc} + \ cdots}

es bastante bueno. Supongamos que U (T (ξ)) forman una representación no proyectiva, es decir,

{\ Displaystyle U (T ({\ bar {\ xi}})) U (T (\ xi)) = U (T (f ({\ bar {\ xi}}, \ xi))).}

La expansión de f a la segunda potencia es

{\ Displaystyle f ^ {a} ({\ bar {\ xi}}, \ xi) = \ xi ^ {a} + {\ bar {\ xi}} ^ {a} + \ sum _ {b, c} f ^ {abc} {\ bar {\ xi}} ^ {b} \ xi ^ {c}.}

Después de expandir la ecuación de multiplicación de representación e igualar coeficientes, tenemos la condición no trivial

{\ Displaystyle t_ {bc} = - t_ {b} t_ {c} -i \ sum _ {a} f ^ {abc} t_ {a}.}

Dado que por definición es simétrico en sus índices, tenemos el conmutador estándar de álgebra de Lie : ${\ Displaystyle t_ {ab}}$

{\ Displaystyle [t_ {b}, t_ {c}] = i \ sum _ {a} (- f ^ {abc} + f ^ {acb}) t_ {a} = i \ sum _ {a} C ^ {abc} t_ {a},}

con C la estructura constante . Los generadores de traducciones son operadores de derivadas parciales, que conmutan:

{\ estilo de visualización \ izquierda [{\ frac {\ parcial} {\ parcial x ^ {b}}}, {\ frac {\ parcial} {\ parcial x ^ {c}}} \ derecha] = 0.}

Esto implica que las constantes de la estructura se desvanecen y, por lo tanto, los coeficientes cuadráticos en la expansión f también se desvanecen. Esto significa que f es simplemente aditivo:

{\ Displaystyle f _ {\ text {abelian}} ^ {a} ({\ bar {\ xi}}, \ xi) = \ xi ^ {a} + {\ bar {\ xi}} ^ {a},}

y así para los grupos abelianos,

{\ Displaystyle U (T ({\ bar {\ xi}})) U (T (\ xi)) = U (T ({\ bar {\ xi}} + \ xi)).}

QED

Rotaciones

El operador de rotación también contiene una derivada direccional. El operador de rotación para un ángulo θ , es decir, por una cantidad θ = | θ | sobre un eje paralelo a es ${\ displaystyle {\ hat {\ theta}} = {\ boldsymbol {\ theta}} / \ theta}$

{\ Displaystyle U (R (\ mathbf {\ theta})) = \ exp (-i \ mathbf {\ theta} \ cdot \ mathbf {L}).}

Aquí L es el operador vectorial que genera SO (3) :

{\ displaystyle \ mathbf {L} = {\ begin {pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \ end {pmatrix}} \ mathbf {i} + {\ begin {pmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \ end {pmatrix}} \ mathbf {j} + {\ begin {pmatrix} 0 & 1 & 0 \\ - 1 & 0 & 0 \\ 0 & 0 & 0 \ end {pmatrix}} \ mathbf {k}.}

Puede mostrarse geométricamente que una rotación infinitesimal a la derecha cambia el vector de posición x por

{\ Displaystyle \ mathbf {x} \ rightarrow \ mathbf {x} - \ delta {\ boldsymbol {\ theta}} \ times \ mathbf {x}.}

Entonces esperaríamos bajo rotación infinitesimal:

{\ Displaystyle U (R (\ delta {\ boldsymbol {\ theta}})) f (\ mathbf {x}) = f (\ mathbf {x} - \ delta {\ boldsymbol {\ theta}} \ times \ mathbf {x}) = f (\ mathbf {x}) - (\ delta {\ boldsymbol {\ theta}} \ times \ mathbf {x}) \ cdot \ nabla f.}

Resulta que

{\ Displaystyle U (R (\ delta \ mathbf {\ theta})) = 1 - (\ delta \ mathbf {\ theta} \ times \ mathbf {x}) \ cdot \ nabla.}

Siguiendo el mismo procedimiento de exponenciación anterior, llegamos al operador de rotación en la base de posición, que es una derivada direccional exponenciada:

{\ Displaystyle U (R (\ mathbf {\ theta})) = \ exp (- (\ mathbf {\ theta} \ times \ mathbf {x}) \ cdot \ nabla).}

Derivada normal

Una derivada normal es una derivada direccional tomada en la dirección normal (es decir, ortogonal ) a alguna superficie en el espacio, o más generalmente a lo largo de un campo vectorial normal ortogonal a alguna hipersuperficie . Véase, por ejemplo, la condición de contorno de Neumann . Si la dirección normal se denota por , entonces la derivada normal de una función f a veces se denota como . En otras notaciones, ${\ Displaystyle \ mathbf {n}}$ ${\ Displaystyle {\ frac {\ parcial f} {\ parcial \ mathbf {n}}}}$

{\ Displaystyle {\ frac {\ parcial f} {\ parcial \ mathbf {n}}} = \ nabla f (\ mathbf {x}) \ cdot \ mathbf {n} = \ nabla _ {\ mathbf {n}} {f} (\ mathbf {x}) = {\ frac {\ parcial f} {\ parcial \ mathbf {x}}} \ cdot \ mathbf {n} = Df (\ mathbf {x}) [\ mathbf {n }].}

En la mecánica continua de sólidos

Varios resultados importantes en la mecánica del continuo requieren las derivadas de vectores con respecto a vectores y de tensores con respecto a vectores y tensores. La directiva direccional proporciona una forma sistemática de encontrar estas derivadas.

Las definiciones de derivadas direccionales para diversas situaciones se dan a continuación. Se supone que las funciones son lo suficientemente suaves como para poder tomar derivadas.

Derivadas de funciones de vectores con valores escalares

Sea f ( v ) una función con valor real del vector v. Entonces la derivada de f (v) con respecto a v (o en v) es el vector definido a través de su producto escalar con cualquier vector u siendo

{\ Displaystyle {\ frac {\ parcial f} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} = Df (\ mathbf {v}) [\ mathbf {u}] = \ left [{\ frac {\ rm {d}} {{\ rm {d}} \ alpha}} ~ f (\ mathbf {v} + \ alpha ~ \ mathbf {u}) \ right] _ {\ alpha = 0}}

para todos los vectores u. El producto escalar anterior produce un escalar, y si u es un vector unitario da la derivada direccional de f en v, en la dirección u.

Propiedades:

Si entonces ${\ Displaystyle f (\ mathbf {v}) = f_ {1} (\ mathbf {v}) + f_ {2} (\ mathbf {v})}$ ${\ estilo de visualización {\ frac {\ f parcial} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} = \ izquierda ({\ frac {\ f_ parcial {1}} {\ parcial \ mathbf {v }}} + {\ frac {\ parcial f_ {2}} {\ parcial \ mathbf {v}}} \ derecha) \ cdot \ mathbf {u}}$
Si entonces ${\ Displaystyle f (\ mathbf {v}) = f_ {1} (\ mathbf {v}) ~ f_ {2} (\ mathbf {v})}$ ${\ estilo de visualización {\ frac {\ f parcial} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} = \ izquierda ({\ frac {\ f_ parcial {1}} {\ parcial \ mathbf {v }}} \ cdot \ mathbf {u} \ right) ~ f_ {2} (\ mathbf {v}) + f_ {1} (\ mathbf {v}) ~ \ left ({\ frac {\ parcial f_ {2 }} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} \ derecha)}$
Si entonces ${\ Displaystyle f (\ mathbf {v}) = f_ {1} (f_ {2} (\ mathbf {v}))}$ ${\ Displaystyle {\ frac {\ parcial f} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} = {\ frac {\ parcial f_ {1}} {\ parcial f_ {2}}} ~ {\ frac {\ parcial f_ {2}} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u}}$

Derivadas de funciones vectoriales de vectores

Sea f (v) una función de valor vectorial del vector v.Entonces la derivada de f (v) con respecto a v (o en v) es el tensor de segundo orden definido a través de su producto escalar con cualquier vector u siendo

{\ Displaystyle {\ frac {\ parcial \ mathbf {f}} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} = D \ mathbf {f} (\ mathbf {v}) [\ mathbf { u}] = \ left [{\ frac {\ rm {d}} {{\ rm {d}} \ alpha}} ~ \ mathbf {f} (\ mathbf {v} + \ alpha ~ \ mathbf {u} ) \ right] _ {\ alpha = 0}}

para todos los vectores u. El producto escalar anterior produce un vector, y si u es un vector unitario da la derivada de dirección de f en v, en la dirección u.

Propiedades:

Si entonces ${\ Displaystyle \ mathbf {f} (\ mathbf {v}) = \ mathbf {f} _ {1} (\ mathbf {v}) + \ mathbf {f} _ {2} (\ mathbf {v})}$ ${\ estilo de visualización {\ frac {\ parcial \ mathbf {f}} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} = \ izquierda ({\ frac {\ parcial \ mathbf {f} _ {1 }} {\ parcial \ mathbf {v}}} + {\ frac {\ parcial \ mathbf {f} _ {2}} {\ parcial \ mathbf {v}}} \ derecha) \ cdot \ mathbf {u}}$
Si entonces ${\ Displaystyle \ mathbf {f} (\ mathbf {v}) = \ mathbf {f} _ {1} (\ mathbf {v}) \ times \ mathbf {f} _ {2} (\ mathbf {v}) }$ ${\ estilo de visualización {\ frac {\ parcial \ mathbf {f}} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} = \ izquierda ({\ frac {\ parcial \ mathbf {f} _ {1 }} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} \ derecha) \ veces \ mathbf {f} _ {2} (\ mathbf {v}) + \ mathbf {f} _ {1} (\ mathbf {v}) \ veces \ izquierda ({\ frac {\ parcial \ mathbf {f} _ {2}} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} \ derecha)}$
Si entonces ${\ Displaystyle \ mathbf {f} (\ mathbf {v}) = \ mathbf {f} _ {1} (\ mathbf {f} _ {2} (\ mathbf {v}))}$ ${\ Displaystyle {\ frac {\ parcial \ mathbf {f}} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u} = {\ frac {\ parcial \ mathbf {f} _ {1}} { \ parcial \ mathbf {f} _ {2}}} \ cdot \ left ({\ frac {\ parcial \ mathbf {f} _ {2}} {\ parcial \ mathbf {v}}} \ cdot \ mathbf {u } \Derecha)}$

Derivadas de funciones escalares valoradas de tensores de segundo orden

Sea una función de valor real del tensor de segundo orden . Entonces la derivada de con respecto a (o en ) en la dirección es el tensor de segundo orden definido como ${\ displaystyle f ({\ boldsymbol {S}})}$ ${\ displaystyle {\ boldsymbol {S}}}$ ${\ displaystyle f ({\ boldsymbol {S}})}$ ${\ displaystyle {\ boldsymbol {S}}}$ ${\ displaystyle {\ boldsymbol {S}}}$ ${\ displaystyle {\ boldsymbol {T}}}$

{\ displaystyle {\ frac {\ parcial f} {\ parcial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = Df ({\ boldsymbol {S}}) [{\ boldsymbol {T}} ] = \ left [{\ frac {\ rm {d}} {{\ rm {d}} \ alpha}} ~ f ({\ boldsymbol {S}} + \ alpha ~ {\ boldsymbol {T}}) \ derecha] _ {\ alpha = 0}}

para todos los tensores de segundo orden . ${\ displaystyle {\ boldsymbol {T}}}$

Propiedades:

Si entonces ${\ displaystyle f ({\ boldsymbol {S}}) = f_ {1} ({\ boldsymbol {S}}) + f_ {2} ({\ boldsymbol {S}})}$ ${\ Displaystyle {\ frac {\ partial f} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = \ left ({\ frac {\ partial f_ {1}} {\ partial { \ boldsymbol {S}}}} + {\ frac {\ parcial f_ {2}} {\ parcial {\ boldsymbol {S}}}} \ derecha): {\ boldsymbol {T}}}$
Si entonces ${\ displaystyle f ({\ boldsymbol {S}}) = f_ {1} ({\ boldsymbol {S}}) ~ f_ {2} ({\ boldsymbol {S}})}$ ${\ Displaystyle {\ frac {\ partial f} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = \ left ({\ frac {\ partial f_ {1}} {\ partial { \ boldsymbol {S}}}}: {\ boldsymbol {T}} \ right) ~ f_ {2} ({\ boldsymbol {S}}) + f_ {1} ({\ boldsymbol {S}}) ~ \ left ({\ frac {\ parcial f_ {2}} {\ parcial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} \ right)}$
Si entonces ${\ Displaystyle f ({\ boldsymbol {S}}) = f_ {1} (f_ {2} ({\ boldsymbol {S}}))}$ ${\ Displaystyle {\ frac {\ partial f} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = {\ frac {\ partial f_ {1}} {\ partial f_ {2} }} ~ \ izquierda ({\ frac {\ parcial f_ {2}} {\ parcial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} \ derecha)}$

Derivadas de funciones con valor tensorial de tensores de segundo orden

Sea una función tensorial de segundo orden del tensor de segundo orden . Entonces la derivada de con respecto a (o en ) en la dirección es el tensor de cuarto orden definido como ${\ displaystyle {\ boldsymbol {F}} ({\ boldsymbol {S}})}$ ${\ displaystyle {\ boldsymbol {S}}}$ ${\ displaystyle {\ boldsymbol {F}} ({\ boldsymbol {S}})}$ ${\ displaystyle {\ boldsymbol {S}}}$ ${\ displaystyle {\ boldsymbol {S}}}$ ${\ displaystyle {\ boldsymbol {T}}}$

{\ displaystyle {\ frac {\ partial {\ boldsymbol {F}}} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = D {\ boldsymbol {F}} ({\ boldsymbol {S}}) [{\ boldsymbol {T}}] = \ left [{\ frac {\ rm {d}} {{\ rm {d}} \ alpha}} ~ {\ boldsymbol {F}} ({ \ boldsymbol {S}} + \ alpha ~ {\ boldsymbol {T}}) \ right] _ {\ alpha = 0}}

para todos los tensores de segundo orden . ${\ displaystyle {\ boldsymbol {T}}}$

Propiedades:

Si entonces ${\ displaystyle {\ boldsymbol {F}} ({\ boldsymbol {S}}) = {\ boldsymbol {F}} _ {1} ({\ boldsymbol {S}}) + {\ boldsymbol {F}} _ { 2} ({\ boldsymbol {S}})}$ ${\ displaystyle {\ frac {\ partial {\ boldsymbol {F}}} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = \ left ({\ frac {\ partial {\ boldsymbol {F}} _ {1}} {\ parcial {\ boldsymbol {S}}}} + {\ frac {\ parcial {\ boldsymbol {F}} _ {2}} {\ parcial {\ boldsymbol {S}} }} \ derecha): {\ boldsymbol {T}}}$
Si entonces ${\ displaystyle {\ boldsymbol {F}} ({\ boldsymbol {S}}) = {\ boldsymbol {F}} _ {1} ({\ boldsymbol {S}}) \ cdot {\ boldsymbol {F}} _ {2} ({\ boldsymbol {S}})}$ ${\ displaystyle {\ frac {\ parcial {\ boldsymbol {F}}} {\ parcial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = \ left ({\ frac {\ partial {\ boldsymbol {F}} _ {1}} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} \ right) \ cdot {\ boldsymbol {F}} _ {2} ({\ boldsymbol { S}}) + {\ boldsymbol {F}} _ {1} ({\ boldsymbol {S}}) \ cdot \ left ({\ frac {\ partial {\ boldsymbol {F}} _ {2}} {\ parcial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} \ right)}$
Si entonces ${\ displaystyle {\ boldsymbol {F}} ({\ boldsymbol {S}}) = {\ boldsymbol {F}} _ {1} ({\ boldsymbol {F}} _ {2} ({\ boldsymbol {S} }))}$ ${\ displaystyle {\ frac {\ partial {\ boldsymbol {F}}} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = {\ frac {\ partial {\ boldsymbol {F} } _ {1}} {\ partial {\ boldsymbol {F}} _ {2}}}: \ left ({\ frac {\ partial {\ boldsymbol {F}} _ {2}} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} \ right)}$
Si entonces ${\ displaystyle f ({\ boldsymbol {S}}) = f_ {1} ({\ boldsymbol {F}} _ {2} ({\ boldsymbol {S}}))}$ ${\ Displaystyle {\ frac {\ partial f} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T}} = {\ frac {\ partial f_ {1}} {\ partial {\ boldsymbol { F}} _ {2}}}: \ left ({\ frac {\ partial {\ boldsymbol {F}} _ {2}} {\ partial {\ boldsymbol {S}}}}: {\ boldsymbol {T} }\Derecha)}$

Ver también

Notas

Referencias

Hildebrand, FB (1976). Cálculo avanzado para aplicaciones . Prentice Hall. ISBN 0-13-011189-9.
KF Riley; MP Hobson; SJ Bence (2010). Métodos matemáticos para la física y la ingeniería . Prensa de la Universidad de Cambridge. ISBN 978-0-521-86153-3.
Shapiro, A. (1990). "Sobre conceptos de diferenciabilidad direccional". Revista de teoría y aplicaciones de la optimización . 66 (3): 477–487. doi : 10.1007 / BF00940933 .

enlaces externos

Medios relacionados con la derivada direccional en Wikimedia Commons

Derivadas direccionales en MathWorld .
Derivada direccional en PlanetMath .

Languages

In other projects

Derivado direccional - Directional derivative

Contenido

Definición

Para funciones diferenciables

Usando solo la dirección del vector

Restricción a un vector unitario

Propiedades

En geometría diferencial

La derivada de la mentira

El tensor de Riemann

En teoría de grupos

Traducciones

Rotaciones

Derivada normal

En la mecánica continua de sólidos

Derivadas de funciones de vectores con valores escalares

Derivadas de funciones vectoriales de vectores

Derivadas de funciones escalares valoradas de tensores de segundo orden

Derivadas de funciones con valor tensorial de tensores de segundo orden

Ver también

Notas

Referencias

enlaces externos