Regla de L'Hôpital - L'Hôpital's rule

Ejemplo de aplicación de la regla de l'Hôpital af ( x ) = sin ( x ) y g ( x ) = −0,5 x : la función h ( x ) = f ( x ) / g ( x ) no está definida en x = 0 , pero se puede completar a una función continua en todo R definiendo h (0) = f ′ (0) / g ′ (0) = −2 .

En las matemáticas , más específicamente el cálculo , la regla de L'Hôpital o regla de L'Hopital ( Francés:  [Lopital] , en inglés: / ˌ l oʊ p i t ɑː l / , loh-pee- TAHL ) es un teorema que proporciona una técnica evaluar límites de formas indeterminadas . La aplicación (o la aplicación repetida) de la regla a menudo convierte una forma indeterminada en una expresión que se puede evaluar fácilmente mediante sustitución. La regla lleva el nombre del matemático francés del siglo XVII Guillaume de l'Hôpital . Aunque la regla se atribuye a menudo a L'Hôpital, el teorema le fue presentado por primera vez en 1694 por el matemático suizo Johann Bernoulli .

Estados regla de L'Hôpital que para las funciones f y g , que son diferenciables en una abierta intervalo I excepto posiblemente en un punto c contenidas en I , si y para todos x en I con x ≠ c , y existe, entonces ${\ textstyle \ lim _ {x \ to c} f (x) = \ lim _ {x \ to c} g (x) = 0 {\ text {o}} \ pm \ infty,}$${\ textstyle g '(x) \ neq 0}$${\ textstyle \ lim _ {x \ to c} {\ frac {f '(x)} {g' (x)}}}$

${\ Displaystyle \ lim _ {x \ to c} {\ frac {f (x)} {g (x)}} = \ lim _ {x \ to c} {\ frac {f '(x)} {g '(X)}}.}$

La diferenciación del numerador y el denominador a menudo simplifica el cociente o lo convierte en un límite que se puede evaluar directamente.

Historia

Guillaume de l'Hôpital (también escrito l'Hospital) publicó esta regla en su libro de 1696 Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes (traducción literal: Análisis de lo infinitamente pequeño para la comprensión de líneas curvas ), el primer libro de texto sobre cálculo diferencial . Sin embargo, se cree que la regla fue descubierta por el matemático suizo Johann Bernoulli .

Forma general

La forma general de la regla de L'Hôpital cubre muchos casos. Deje C y L se extendieron números reales (es decir, números reales, infinito positivo, o infinito negativo). Sea I un intervalo abierto que contiene c (para un límite de dos lados) o un intervalo abierto con el punto final c (para un límite unilateral , o un límite en el infinito si c es infinito). Se supone que las funciones de valor real f y g son diferenciables en I excepto posiblemente en c , y adicionalmente en I excepto posiblemente en c . También se supone que, por lo tanto, la regla se aplica a situaciones en las que la razón de las derivadas tiene un límite finito o infinito, pero no a situaciones en las que esa razón fluctúa permanentemente a medida que x se acerca cada vez más a c . ${\ Displaystyle g '(x) \ neq 0}$${\ Displaystyle \ lim _ {x \ to c} {\ frac {f '(x)} {g' (x)}} = L.}$

Si alguno

${\ Displaystyle \ lim _ {x \ to c} f (x) = \ lim _ {x \ to c} g (x) = 0}$

o

${\ Displaystyle \ lim _ {x \ to c} | f (x) | = \ lim _ {x \ to c} | g (x) | = \ infty,}$

luego

${\ Displaystyle \ lim _ {x \ to c} {\ frac {f (x)} {g (x)}} = L.}$

Aunque hemos escrito x  → c en todas partes, los límites también pueden ser los límites de un solo lado ( x  → c ⁺ o x  → c ^- ), cuando c es un punto final finito de I .

En el segundo caso, la hipótesis de que f diverge hasta el infinito no se usa en la demostración (ver nota al final de la sección de prueba); así, mientras que las condiciones de la regla normalmente se establecen como arriba, la segunda condición suficiente para que el procedimiento de la regla sea válido se puede enunciar más brevemente como${\ Displaystyle \ lim _ {x \ to c} | g (x) | = \ infty.}$

La hipótesis que aparece con mayor frecuencia en la literatura, pero algunos autores eluden esta hipótesis al agregar otras hipótesis en otros lugares. Un método consiste en definir el límite de una función con el requisito adicional de que la función limitante se defina en todas partes en el intervalo relevante I excepto posiblemente en c . Otro método es requerir que tanto f como g sean diferenciables en todas partes en un intervalo que contenga c . ${\ Displaystyle g '(x) \ neq 0}$

Requisito de que exista el límite

El requisito de que el límite

${\ Displaystyle \ lim _ {x \ to c} {\ frac {f '(x)} {g' (x)}}}$

existe es esencial. Sin esta condición, o puede presentar oscilaciones no amortiguadas como aproximaciones , en cuyo caso no se aplica la regla de L'Hôpital. Por ejemplo, si , y , entonces ${\ Displaystyle f '}$${\ displaystyle g '}$${\ Displaystyle x}$${\ Displaystyle c}$${\ Displaystyle f (x) = x + \ sin (x)}$${\ Displaystyle g (x) = x}$${\ Displaystyle c = \ pm \ infty}$

${\ Displaystyle {\ frac {f '(x)} {g' (x)}} = {\ frac {1+ \ cos (x)} {1}};}$

esta expresión no se acerca a un límite a medida que avanza , ya que la función coseno oscila entre 1 y -1 . Pero trabajando con las funciones originales, se puede demostrar que existe: ${\ Displaystyle x}$${\ Displaystyle c}$${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {f (x)} {g (x)}}}$

${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {f (x)} {g (x)}} = \ lim _ {x \ to \ infty} \ left (1 + {\ frac {\ sin (x)} {x}} \ right) = 1.}$

En un caso como este, todo lo que se puede concluir es que

${\ Displaystyle \ liminf _ {x \ to c} {\ frac {f '(x)} {g' (x)}} \ leq \ liminf _ {x \ to c} {\ frac {f (x)} {g (x)}} \ leq \ limsup _ {x \ to c} {\ frac {f (x)} {g (x)}} \ leq \ limsup _ {x \ to c} {\ frac {f '(x)} {g' (x)}},}$

de modo que si existe el límite de f / g , entonces debe estar entre los límites inferior y superior de f ′ / g ′. (En el ejemplo anterior, esto es cierto, ya que 1 de hecho se encuentra entre 0 y 2.)

Ejemplos de

• Aquí hay un ejemplo básico que involucra la función exponencial, que involucra la forma indeterminada 0/0en x = 0 :
  $${\ displaystyle {\ begin {alineado} \ lim _ {x \ to 0} {\ frac {e ^ {x} -1} {x ^ {2} + x}} & = \ lim _ {x \ to 0 } {\ frac {{\ frac {d} {dx}} (e ^ {x} -1)} {{\ frac {d} {dx}} (x ^ {2} + x)}} \\ [ 4pt] & = \ lim _ {x \ to 0} {\ frac {e ^ {x}} {2x + 1}} \\ [4pt] & = 1. \ end {alineado}}}$$

  
• Este es un ejemplo más elaborado que involucra 0/0. La aplicación de la regla de L'Hôpital una sola vez todavía resulta en una forma indeterminada. En este caso, el límite puede evaluarse aplicando la regla tres veces:
  $${\ Displaystyle {\ begin {alineado} \ lim _ {x \ to 0} {\ frac {2 \ sin (x) - \ sin (2x)} {x- \ sin (x)}} & = \ lim _ {x \ to 0} {\ frac {2 \ cos (x) -2 \ cos (2x)} {1- \ cos (x)}} \\ [4pt] & = \ lim _ {x \ to 0} {\ frac {-2 \ sin (x) +4 \ sin (2x)} {\ sin (x)}} \\ [4pt] & = \ lim _ {x \ to 0} {\ frac {-2 \ cos (x) +8 \ cos (2x)} {\ cos (x)}} \\ [4pt] & = {\ frac {-2 + 8} {1}} \\ [4pt] & = 6. \ final {alineado}}}$$

  
• Aquí hay un ejemplo que involucra ∞/∞:
  $${\ Displaystyle \ lim _ {x \ to \ infty} x ^ {n} \ cdot e ^ {- x} = \ lim _ {x \ to \ infty} {\ frac {x ^ {n}} {e ^ {x}}} = \ lim _ {x \ to \ infty} {\ frac {nx ^ {n-1}} {e ^ {x}}} = n \ cdot \ lim _ {x \ to \ infty} {\ frac {x ^ {n-1}} {e ^ {x}}}.}$$

  
  Aplique repetidamente la regla de L'Hôpital hasta que el exponente sea cero (si n es un número entero) o negativo (si n es fraccionario) para concluir que el límite es cero.
• Aquí hay un ejemplo que involucra la forma indeterminada 0 · ∞ (ver más abajo), que se reescribe como la forma∞/∞:
  $${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} x \ ln x = \ lim _ {x \ to 0 ^ {+}} {\ frac {\ ln x} {\ frac {1} {x }}} = \ lim _ {x \ to 0 ^ {+}} {\ frac {\ frac {1} {x}} {- {\ frac {1} {x ^ {2}}}}} = \ lim _ {x \ to 0 ^ {+}} - x = 0.}$$

  
• Aquí hay un ejemplo que involucra la fórmula de pago de la hipoteca y0/0. Sea P el principal (monto del préstamo), r la tasa de interés por período yn el número de períodos. Cuando r es cero, el monto de reembolso por período es (ya que solo se reembolsa el principal); esto es coherente con la fórmula para tipos de interés distintos de cero:${\ Displaystyle {\ frac {P} {n}}}$
  $${\ Displaystyle {\ begin {alineado} \ lim _ {r \ to 0} {\ frac {Pr (1 + r) ^ {n}} {(1 + r) ^ {n} -1}} & = P \ lim _ {r \ to 0} {\ frac {(1 + r) ^ {n} + rn (1 + r) ^ {n-1}} {n (1 + r) ^ {n-1}} } \\ [4pt] & = {\ frac {P} {n}}. \ End {alineado}}}$$

  
• También se puede utilizar la regla de L'Hôpital para demostrar el siguiente teorema. Si f es dos veces diferenciable en una vecindad de x y que su segunda derivada es continua en esta vecindad, entonces
  $${\ Displaystyle {\ begin {alineado} \ lim _ {h \ to 0} {\ frac {f (x + h) + f (xh) -2f (x)} {h ^ {2}}} & = \ lim _ {h \ to 0} {\ frac {f '(x + h) -f' (xh)} {2h}} \\ [4pt] & = \ lim _ {h \ to 0} {\ frac { f '' (x + h) + f '' (xh)} {2}} \\ [4pt] & = f '' (x). \ end {alineado}}}$$

  

• A veces, la regla de L'Hôpital se invoca de una manera engañosa: suponga que f  ( x ) + f  ′ ( x ) converge cuando x → ∞ y que converge al infinito positivo o negativo. Luego:${\ Displaystyle e ^ {x} \ cdot f (x)}$

  $${\ Displaystyle \ lim _ {x \ to \ infty} f (x) = \ lim _ {x \ to \ infty} {\ frac {e ^ {x} \ cdot f (x)} {e ^ {x} }} = \ lim _ {x \ to \ infty} {\ frac {e ^ {x} {\ bigl (} f (x) + f '(x) {\ bigr)}} {e ^ {x}} } = \ lim _ {x \ to \ infty} {\ bigl (} f (x) + f '(x) {\ bigr)}}$$

  
  y así, existe y${\ textstyle \ lim _ {x \ to \ infty} f (x)}$${\ textstyle \ lim _ {x \ to \ infty} f '(x) = 0.}$

  El resultado permanece verdadero sin la hipótesis agregada que converge al infinito positivo o negativo, pero la justificación es entonces incompleta.${\ Displaystyle e ^ {x} \ cdot f (x)}$

Complicaciones

A veces, la regla de L'Hôpital no conduce a una respuesta en un número finito de pasos a menos que se apliquen algunos pasos adicionales. Los ejemplos incluyen lo siguiente:

• Dos aplicaciones pueden conducir a un retorno a la expresión original que se iba a evaluar:
  $${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {e ^ {x} + e ^ {- x}} {e ^ {x} -e ^ {- x}}} = \ lim _ { x \ to \ infty} {\ frac {e ^ {x} -e ^ {- x}} {e ^ {x} + e ^ {- x}}} = \ lim _ {x \ to \ infty} { \ frac {e ^ {x} + e ^ {- x}} {e ^ {x} -e ^ {- x}}} = \ cdots.}$$

  
  Esta situación puede resolverse sustituyendo y observando que y va al infinito cuando x va al infinito; con esta sustitución, este problema se puede solucionar con una sola aplicación de la regla:${\ Displaystyle y = e ^ {x}}$
  $${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {e ^ {x} + e ^ {- x}} {e ^ {x} -e ^ {- x}}} = \ lim _ { y \ to \ infty} {\ frac {y + y ^ {- 1}} {yy ^ {- 1}}} = \ lim _ {y \ to \ infty} {\ frac {1-y ^ {- 2 }} {1 + y ^ {- 2}}} = {\ frac {1} {1}} = 1.}$$

  
  Alternativamente, el numerador y el denominador se pueden multiplicar por, momento en el que la regla de L'Hôpital se puede aplicar inmediatamente con éxito:${\ Displaystyle e ^ {x},}$
  $${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {e ^ {x} + e ^ {- x}} {e ^ {x} -e ^ {- x}}} = \ lim _ { x \ to \ infty} {\ frac {e ^ {2x} +1} {e ^ {2x} -1}} = \ lim _ {x \ to \ infty} {\ frac {2e ^ {2x}} { 2e ^ {2x}}} = 1.}$$

  
• Es posible que una cantidad arbitrariamente grande de aplicaciones nunca dé lugar a una respuesta, incluso sin repetir:
  $${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {x ^ {\ frac {1} {2}} + x ^ {- {\ frac {1} {2}}}} {x ^ { \ frac {1} {2}} - x ^ {- {\ frac {1} {2}}}}} = \ lim _ {x \ to \ infty} {\ frac {{\ frac {1} {2 }} x ^ {- {\ frac {1} {2}}} - {\ frac {1} {2}} x ^ {- {\ frac {3} {2}}}} {{\ frac {1 } {2}} x ^ {- {\ frac {1} {2}}} + {\ frac {1} {2}} x ^ {- {\ frac {3} {2}}}}} = \ lim _ {x \ to \ infty} {\ frac {- {\ frac {1} {4}} x ^ {- {\ frac {3} {2}}} + {\ frac {3} {4}} x ^ {- {\ frac {5} {2}}}} {- {\ frac {1} {4}} x ^ {- {\ frac {3} {2}}} - {\ frac {3} {4}} x ^ {- {\ frac {5} {2}}}}} = \ cdots.}$$

  
  Esta situación también se puede abordar mediante una transformación de variables, en este caso :${\ Displaystyle y = {\ sqrt {x}}}$
  $${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {x ^ {\ frac {1} {2}} + x ^ {- {\ frac {1} {2}}}} {x ^ { \ frac {1} {2}} - x ^ {- {\ frac {1} {2}}}}} = \ lim _ {y \ to \ infty} {\ frac {y + y ^ {- 1} } {yy ^ {- 1}}} = \ lim _ {y \ to \ infty} {\ frac {1-y ^ {- 2}} {1 + y ^ {- 2}}} = {\ frac { 1} {1}} = 1.}$$

  
  Nuevamente, un enfoque alternativo es multiplicar el numerador y el denominador por antes de aplicar la regla de L'Hôpital:${\ Displaystyle x ^ {1/2}}$
  $${\ Displaystyle \ lim _ {x \ to \ infty} {\ frac {x ^ {\ frac {1} {2}} + x ^ {- {\ frac {1} {2}}}} {x ^ { \ frac {1} {2}} - x ^ {- {\ frac {1} {2}}}}} = \ lim _ {x \ to \ infty} {\ frac {x + 1} {x-1 }} = \ lim _ {x \ to \ infty} {\ frac {1} {1}} = 1.}$$

  

Un error común es usar la regla de L'Hôpital con un razonamiento circular para calcular una derivada a través de un cociente de diferencias . Por ejemplo, considere la tarea de probar la fórmula derivada para potencias de x :

${\ Displaystyle \ lim _ {h \ to 0} {\ frac {(x + h) ^ {n} -x ^ {n}} {h}} = nx ^ {n-1}.}$

Aplicando la regla de L'Hôpital y encontrando las derivadas con respecto a h del numerador y el denominador, se obtiene nx ^{n −1} como se esperaba. Sin embargo, diferenciar el numerador requería el uso del mismo hecho que se está probando. Este es un ejemplo de la petición de principio , ya que no se puede asumir que el hecho está probado durante el curso de la prueba.

Contraejemplos cuando la derivada del denominador es cero

La necesidad de la condición de que cerca se puede ver en el siguiente contraejemplo debido a Otto Stolz . Let y Then no hay límite para como Sin embargo, ${\ Displaystyle g '(x) \ neq 0}$${\ Displaystyle c}$${\ Displaystyle f (x) = x + \ sin x \ cos x}$${\ Displaystyle g (x) = f (x) e ^ {\ sin x}.}$${\ Displaystyle f (x) / g (x)}$${\ Displaystyle x \ to \ infty.}$

${\ Displaystyle {\ begin {alineado} {\ frac {f '(x)} {g' (x)}} & = {\ frac {2 \ cos ^ {2} x} {(2 \ cos ^ {2 } x) e ^ {\ sin x} + (x + \ sin x \ cos x) e ^ {\ sin x} \ cos x}} \\ [4pt] & = {\ frac {2 \ cos x} {2 \ cos x + x + \ sin x \ cos x}} e ^ {- \ sin x}, \ end {alineado}}}$

que tiende a 0 como . Ralph P. Boas Jr. encontró más ejemplos de este tipo .${\ Displaystyle x \ to \ infty}$

Otras formas indeterminadas

Otras formas indeterminadas, como 1 ^∞ , 0 ⁰ , ∞ ⁰ , 0 · ∞ y ∞ - ∞ , a veces se pueden evaluar utilizando la regla de L'Hôpital. Por ejemplo, para evaluar un límite que involucre ∞ - ∞ , convierta la diferencia de dos funciones en un cociente:

${\ displaystyle {\ begin {alineado} \ lim _ {x \ to 1} \ left ({\ frac {x} {x-1}} - {\ frac {1} {\ ln x}} \ right) y = \ lim _ {x \ to 1} {\ frac {x \ cdot \ ln x-x + 1} {(x-1) \ cdot \ ln x}} & \ quad (1) \\ [6pt] & = \ lim _ {x \ to 1} {\ frac {\ ln x} {{\ frac {x-1} {x}} + \ ln x}} & \ quad (2) \\ [6pt] & = \ lim _ {x \ to 1} {\ frac {x \ cdot \ ln x} {x-1 + x \ cdot \ ln x}} & \ quad (3) \\ [6pt] & = \ lim _ { x \ a 1} {\ frac {1+ \ ln x} {1 + 1 + \ ln x}} & \ quad (4) \\ [6pt] & = \ lim _ {x \ a 1} {\ frac {1+ \ ln x} {2+ \ ln x}} \\ [6pt] & = {\ frac {1} {2}}, \ end {alineado}}}$

donde se aplica la regla de L'Hôpital al pasar de (1) a (2) y de nuevo al pasar de (3) a (4).

La regla de L'Hôpital se puede usar en formas indeterminadas que involucran exponentes usando logaritmos para "mover el exponente hacia abajo". Aquí hay un ejemplo que involucra la forma indeterminada 0 ⁰ :

${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} x ^ {x} = \ lim _ {x \ to 0 ^ {+}} e ^ {\ ln (x ^ {x})} = \ lim _ {x \ to 0 ^ {+}} e ^ {x \ cdot \ ln x} = e ^ {\ lim \ limits _ {x \ to 0 ^ {+}} (x \ cdot \ ln x)} .}$

Es válido mover el límite dentro de la función exponencial porque la función exponencial es continua . Ahora el exponente se ha "movido hacia abajo". El límite es de la forma indeterminada 0 · ∞ , pero como se muestra en un ejemplo anterior, la regla de l'Hôpital puede usarse para determinar que ${\ Displaystyle x}$${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} x \ cdot \ ln x}$

${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} x \ cdot \ ln x = 0.}$

Por lo tanto

${\ Displaystyle \ lim _ {x \ to 0 ^ {+}} x ^ {x} = e ^ {0} = 1.}$

Teorema de Stolz-Cesàro

El teorema de Stolz-Cesàro es un resultado similar que involucra límites de secuencias, pero usa operadores de diferencias finitas en lugar de derivadas .

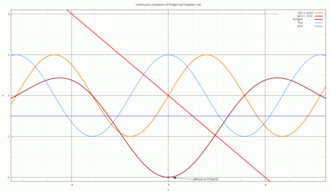
Interpretación geométrica

Considere la curva en el plano cuya coordenada x está dada por g ( t ) y cuya coordenada y está dada por f ( t ) , con ambas funciones continuas, es decir, el lugar geométrico de puntos de la forma [ g ( t ), f ( t )] . Suponga que f ( c ) = g ( c ) = 0 . El límite de la relaciónf ( t )/g ( t )como t → c es la pendiente de la tangente a la curva en el punto [ g ( c ), f ( c )] = [0,0] . La tangente a la curva en el punto [ g ( t ), f ( t )] viene dada por [ g ′ ( t ), f ′ ( t )] . La regla de L'Hôpital establece entonces que la pendiente de la curva cuando t = c es el límite de la pendiente de la tangente a la curva cuando la curva se acerca al origen, siempre que este esté definido.

Prueba de la regla de L'Hôpital

Caso especial

La prueba de la regla de L'Hôpital es simple en el caso en que f y g son continuamente diferenciables en el punto c y donde un límite finito se encuentra después de la primera ronda de la diferenciación. No es una prueba de la regla general de L'Hôpital porque es más estricta en su definición, requiriendo tanto diferenciabilidad como que c sea ​​un número real. Dado que muchas funciones comunes tienen derivadas continuas (por ejemplo , polinomios , seno y coseno , funciones exponenciales ), es un caso especial digno de atención.

Supóngase que f y g son continuamente diferenciable en un número real c , que , y que . Luego ${\ Displaystyle f (c) = g (c) = 0}$${\ Displaystyle g '(c) \ neq 0}$

${\ Displaystyle {\ begin {alineado} & \ lim _ {x \ to c} {\ frac {f (x)} {g (x)}} = \ lim _ {x \ to c} {\ frac {f (x) -0} {g (x) -0}} = \ lim _ {x \ to c} {\ frac {f (x) -f (c)} {g (x) -g (c)} } \\ [6pt] = {} & \ lim _ {x \ to c} {\ frac {\ left ({\ frac {f (x) -f (c)} {xc}} \ right)} {\ izquierda ({\ frac {g (x) -g (c)} {xc}} \ right)}} = {\ frac {\ lim \ limits _ {x \ to c} \ left ({\ frac {f ( x) -f (c)} {xc}} \ right)} {\ lim \ limits _ {x \ to c} \ left ({\ frac {g (x) -g (c)} {xc}} \ derecha)}} = {\ frac {f '(c)} {g' (c)}} = \ lim _ {x \ to c} {\ frac {f '(x)} {g' (x)} }. \ end {alineado}}}$

Esto se sigue de la definición de cociente de diferencias de la derivada. La última igualdad se sigue de la continuidad de las derivadas en c . El límite en la conclusión no es indeterminado porque . ${\ Displaystyle g '(c) \ neq 0}$

La prueba de una versión más general de la regla de L'Hôpital se da a continuación.

Prueba general

La siguiente prueba se debe a Taylor (1952) , donde una prueba unificada de la0/0 y ± ∞/± ∞se dan formas indeterminadas. Taylor señala que se pueden encontrar diferentes pruebas en Lettenmeyer (1936) y Wazewski (1949) .

Vamos f y g son funciones que satisfacen las hipótesis en la forma general sección. Sea el intervalo abierto en la hipótesis con el punto final c . Teniendo en cuenta que en este intervalo yg es continuo, se puede elegir más pequeño para que g sea ​​distinto de cero . ${\ Displaystyle {\ mathcal {I}}}$${\ Displaystyle g '(x) \ neq 0}$${\ Displaystyle {\ mathcal {I}}}$${\ Displaystyle {\ mathcal {I}}}$

Para cada x en el intervalo, defina y como rangos sobre todos los valores entre x y c . (Los símbolos inf y sup denotan el infimum y supremum ). ${\ Displaystyle m (x) = \ inf {\ frac {f '(\ xi)} {g' (\ xi)}}}$${\ Displaystyle M (x) = \ sup {\ frac {f '(\ xi)} {g' (\ xi)}}}$${\ Displaystyle \ xi}$

De la diferenciabilidad de f y g en , valor teorema de Cauchy asegura que para dos puntos distintos x y y en existe una entre x y y de tal manera que . En consecuencia, para todas las opciones de x e y distintas en el intervalo. El valor de g ( x ) - g ( Y ) es siempre distinto de cero para distinta x y y en el intervalo, por si no lo era, el valor medio teorema implicaría la existencia de un p entre x y y de tal manera que g' ( p ) = 0. ${\ Displaystyle {\ mathcal {I}}}$${\ Displaystyle {\ mathcal {I}}}$${\ Displaystyle \ xi}$${\ Displaystyle {\ frac {f (x) -f (y)} {g (x) -g (y)}} = {\ frac {f '(\ xi)} {g' (\ xi)}} }$${\ Displaystyle m (x) \ leq {\ frac {f (x) -f (y)} {g (x) -g (y)}} \ leq M (x)}$

La definición de m ( x ) y M ( x ) dará como resultado un número real extendido, por lo que es posible que adopten los valores ± ∞. En los dos casos siguientes, m ( x ) y M ( x ) establecerán límites en la relaciónF/gramo.

Caso 1: ${\ Displaystyle \ lim _ {x \ to c} f (x) = \ lim _ {x \ to c} g (x) = 0}$

Para cualquier x en el intervalo , y el punto y entre x y c , ${\ Displaystyle {\ mathcal {I}}}$

${\ Displaystyle m (x) \ leq {\ frac {f (x) -f (y)} {g (x) -g (y)}} = {\ frac {{\ frac {f (x)} { g (x)}} - {\ frac {f (y)} {g (x)}}} {1 - {\ frac {g (y)} {g (x)}}}} \ leq M (x )}$

y por lo tanto cuando y se acerca a c , y se vuelve cero, y así ${\ Displaystyle {\ frac {f (y)} {g (x)}}}$${\ Displaystyle {\ frac {g (y)} {g (x)}}}$

${\ Displaystyle m (x) \ leq {\ frac {f (x)} {g (x)}} \ leq M (x).}$

Caso 2: ${\ Displaystyle \ lim _ {x \ to c} | g (x) | = \ infty}$

Para cada x en el intervalo , defina . Para cada punto y entre x y c , ${\ Displaystyle {\ mathcal {I}}}$${\ displaystyle S_ {x} = \ {y \ mid y {\ text {está entre}} x {\ text {y}} c \}}$

${\ Displaystyle m (x) \ leq {\ frac {f (y) -f (x)} {g (y) -g (x)}} = {\ frac {{\ frac {f (y)} { g (y)}} - {\ frac {f (x)} {g (y)}}} {1 - {\ frac {g (x)} {g (y)}}}} \ leq M (x ).}$

Cuando y se acerca a c , ambos y se vuelven cero, y por lo tanto ${\ Displaystyle {\ frac {f (x)} {g (y)}}}$${\ Displaystyle {\ frac {g (x)} {g (y)}}}$

${\ Displaystyle m (x) \ leq \ liminf _ {y \ in S_ {x}} {\ frac {f (y)} {g (y)}} \ leq \ limsup _ {y \ in S_ {x} } {\ frac {f (y)} {g (y)}} \ leq M (x).}$

El límite superior y el límite inferior son necesarios ya que la existencia del límite deF/gramo aún no se ha establecido.

También es el caso que

${\ Displaystyle \ lim _ {x \ to c} m (x) = \ lim _ {x \ to c} M (x) = \ lim _ {x \ to c} {\ frac {f '(x)} {g '(x)}} = L.}$

y

${\ Displaystyle \ lim _ {x \ to c} \ left (\ liminf _ {y \ in S_ {x}} {\ frac {f (y)} {g (y)}} \ right) = \ liminf _ {x \ to c} {\ frac {f (x)} {g (x)}}}$ y ${\ Displaystyle \ lim _ {x \ to c} \ left (\ limsup _ {y \ in S_ {x}} {\ frac {f (y)} {g (y)}} \ right) = \ limsup _ {x \ to c} {\ frac {f (x)} {g (x)}}.}$

En el caso 1, el teorema del emparedado establece que existe y es igual a L . En el caso 2, y la contracción del teorema de nuevo afirma que , por lo que el límite existe y es igual a L . Este es el resultado que se iba a demostrar. ${\ Displaystyle \ lim _ {x \ to c} {\ frac {f (x)} {g (x)}}}$${\ Displaystyle \ liminf _ {x \ to c} {\ frac {f (x)} {g (x)}} = \ limsup _ {x \ to c} {\ frac {f (x)} {g ( x)}} = L}$${\ Displaystyle \ lim _ {x \ to c} {\ frac {f (x)} {g (x)}}}$

En el caso 2, la suposición de que f ( x ) diverge hasta el infinito no se utilizó dentro de la demostración. Esto significa que si | g ( x ) | diverge hasta el infinito cuando x se acerca a cy tanto f como g satisfacen las hipótesis de la regla de L'Hôpital, entonces no se necesita ninguna suposición adicional sobre el límite de f ( x ): incluso podría darse el caso de que el límite de f ( x ) no existe. En este caso, el teorema de L'Hopital es en realidad una consecuencia de Cesàro-Stolz.

En el caso de que | g ( x ) | diverge a infinito cuando x se acerca a c y f ( x converge) a un límite finito en c , entonces la regla de L'Hôpital sería aplicable, pero no es absolutamente necesario, ya que el cálculo límite básico demostrará que el límite de f ( x ) / g ( x ) cuando x se acerca a c debe ser cero.

Corolario

Una consecuencia simple pero muy útil de la regla de L'Hopital es un criterio bien conocido de diferenciación. Establece lo siguiente: suponga que f es continua en a , y que existe para todo x en algún intervalo abierto que contenga a , excepto quizás para . Supongamos, además, que existe. Entonces también existe y ${\ Displaystyle f '(x)}$${\ Displaystyle x = a}$${\ Displaystyle \ lim _ {x \ to a} f '(x)}$${\ Displaystyle f '(a)}$

${\ Displaystyle f '(a) = \ lim _ {x \ to a} f' (x).}$

En particular, f ' también es continua en a .

Prueba

Considere las funciones y . La continuidad de f en a nos dice eso . Además, dado que una función polinomial es siempre continua en todas partes. La aplicación de la regla de L'Hopital demuestra eso . ${\ Displaystyle h (x) = f (x) -f (a)}$${\ Displaystyle g (x) = xa}$${\ Displaystyle \ lim _ {x \ to a} h (x) = 0}$${\ Displaystyle \ lim _ {x \ to a} g (x) = 0}$${\ Displaystyle f '(a): = \ lim _ {x \ to a} {\ frac {f (x) -f (a)} {xa}} = \ lim _ {x \ to a} {\ frac {h (x)} {g (x)}} = \ lim _ {x \ to a} f '(x)}$

Ver también

• La controversia de L'Hôpital

Notas

Referencias

Fuentes

• Chatterjee, Dipak (2005), Análisis real , PHI Learning Pvt. Ltd, ISBN 81-203-2678-4
• Krantz, Steven G. (2004), Un manual de variables reales. Con aplicaciones a ecuaciones diferenciales y análisis de Fourier , Boston, MA: Birkhäuser Boston Inc., págs. Xiv + 201, doi : 10.1007 / 978-0-8176-8128-9 , ISBN 0-8176-4329-X, Señor  2015447
• Lettenmeyer, F. (1936), "Über die sogenannte Hospitalsche Regel", Journal für die reine und angewandte Mathematik , 1936 (174): 246–247, doi : 10.1515 / crll.1936.174.246 , S2CID  199546754
• Taylor, AE (1952), "La regla de L'Hospital", Amer. Matemáticas. Mensual , 59 (1): 20-24, doi : 10.2307 / 2307183 , ISSN  0002-9890 , JSTOR  2307183 , MR  0044602
• Wazewski, T. (1949), "Quelques démonstrations uniformes pour tous les cas du théorème de l'Hôpital. Généralisations", Prace Mat.-Fiz. (en francés), 47 : 117–128, MR  0034430