| Operación
|
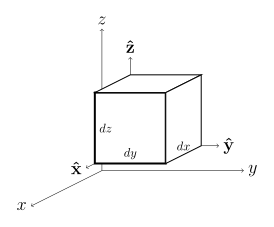
Coordenadas cartesianas ( x , y , z )
|
Coordenadas cilíndricas ( ρ , φ , z )
|
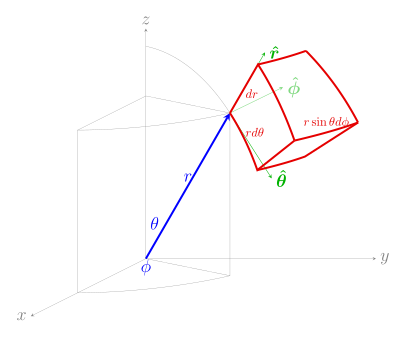
Coordenadas esféricas ( r , θ , φ ) , donde θ es el ángulo polar y φ es el ángulo azimutal
|
|
Campo vectorial A
|

|

|

|
|
Gradiente ∇ f
|

|

|

|
|
Divergencia ∇ ⋅ A
|

|

|

|
|
Curl ∇ × A
|

|

|

|
|
Operador de Laplace ∇ 2 f ≡ ∆ f
|

|

|

|
|
Vector Laplaciano ∇ 2 A ≡ ∆ A
|

|

|

|
|
Derivado material ( A ⋅ ∇) B
|

|

|

|
| Tensor ∇ ⋅ T (no confundir con divergencia de tensor de segundo orden )
|

|
![{\ Displaystyle {\ begin {alineado} \ left [{\ frac {\ parcial T _ {\ rho \ rho}} {\ parcial \ rho}} + {\ frac {1} {\ rho}} {\ frac {\ parcial T _ {\ varphi \ rho}} {\ parcial \ varphi}} + {\ frac {\ parcial T_ {z \ rho}} {\ parcial z}} + {\ frac {1} {\ rho}} (T_ {\ rho \ rho} -T _ {\ varphi \ varphi}) \ right] & {\ hat {\ boldsymbol {\ rho}}} \\ + \ left [{\ frac {\ parcial T _ {\ rho \ varphi} } {\ parcial \ rho}} + {\ frac {1} {\ rho}} {\ frac {\ parcial T _ {\ varphi \ varphi}} {\ parcial \ varphi}} + {\ frac {\ parcial T_ { z \ varphi}} {\ parcial z}} + {\ frac {1} {\ rho}} (T _ {\ rho \ varphi} + T _ {\ varphi \ rho}) \ right] & {\ hat {\ boldsymbol {\ varphi}}} \\ + \ izquierda [{\ frac {\ parcial T _ {\ rho z}} {\ parcial \ rho}} + {\ frac {1} {\ rho}} {\ frac {\ parcial T _ {\ varphi z}} {\ parcial \ varphi}} + {\ frac {\ parcial T_ {zz}} {\ parcial z}} + {\ frac {T _ {\ rho z}} {\ rho}} \ derecha] & {\ hat {\ mathbf {z}}} \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3116bd7e75151c8d599b5e090d2433daffa21069)
|
![{\ Displaystyle {\ begin {alineado} \ left [{\ frac {\ parcial T_ {rr}} {\ parcial r}} + 2 {\ frac {T_ {rr}} {r}} + {\ frac {1 } {r}} {\ frac {\ parcial T _ {\ theta r}} {\ parcial \ theta}} + {\ frac {\ cot \ theta} {r}} T _ {\ theta r} + {\ frac { 1} {r \ sin \ theta}} {\ frac {\ parcial T _ {\ varphi r}} {\ parcial \ varphi}} - {\ frac {1} {r}} (T _ {\ theta \ theta} + T _ {\ varphi \ varphi}) \ right] & {\ hat {\ mathbf {r}}} \\ + \ left [{\ frac {\ parcial T_ {r \ theta}} {\ parcial r}} + 2 {\ frac {T_ {r \ theta}} {r}} + {\ frac {1} {r}} {\ frac {\ parcial T _ {\ theta \ theta}} {\ parcial \ theta}} + {\ frac {\ cot \ theta} {r}} T _ {\ theta \ theta} + {\ frac {1} {r \ sin \ theta}} {\ frac {\ parcial T _ {\ varphi \ theta}} {\ parcial \ varphi}} + {\ frac {T _ {\ theta r}} {r}} - {\ frac {\ cot \ theta} {r}} T _ {\ varphi \ varphi} \ right] & {\ hat {\ símbolo en negrita {\ theta}}} \\ + \ left [{\ frac {\ parcial T_ {r \ varphi}} {\ parcial r}} + 2 {\ frac {T_ {r \ varphi}} {r}} + {\ frac {1} {r}} {\ frac {\ parcial T _ {\ theta \ varphi}} {\ parcial \ theta}} + {\ frac {1} {r \ sin \ theta}} {\ frac { \ parcial T _ {\ varphi \ varphi}} {\ parcial \ varphi}} + {\ frac {T _ {\ var phi r}} {r}} + {\ frac {\ cot \ theta} {r}} (T _ {\ theta \ varphi} + T _ {\ varphi \ theta}) \ right] & {\ hat {\ boldsymbol { \ varphi}}} \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89522d9531233ee5f0a581ec441bb20c337a13b8)
|
| Desplazamiento diferencial d ℓ
|

|

|

|
| Área normal diferencial d S
|

|

|

|
| Volumen diferencial dV
|

|

|

|

![{\ Displaystyle \ theta \ en [0, \ pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c833964ea08aa30df8b6f56664461a5499b38144)
![{\ Displaystyle \ varphi \ in [0,2 \ pi]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adacea8b18fa91c9b01816ed054d2cf4f26b72fb)








































![{\ Displaystyle {\ begin {alineado} \ left [{\ frac {\ parcial T _ {\ rho \ rho}} {\ parcial \ rho}} + {\ frac {1} {\ rho}} {\ frac {\ parcial T _ {\ varphi \ rho}} {\ parcial \ varphi}} + {\ frac {\ parcial T_ {z \ rho}} {\ parcial z}} + {\ frac {1} {\ rho}} (T_ {\ rho \ rho} -T _ {\ varphi \ varphi}) \ right] & {\ hat {\ boldsymbol {\ rho}}} \\ + \ left [{\ frac {\ parcial T _ {\ rho \ varphi} } {\ parcial \ rho}} + {\ frac {1} {\ rho}} {\ frac {\ parcial T _ {\ varphi \ varphi}} {\ parcial \ varphi}} + {\ frac {\ parcial T_ { z \ varphi}} {\ parcial z}} + {\ frac {1} {\ rho}} (T _ {\ rho \ varphi} + T _ {\ varphi \ rho}) \ right] & {\ hat {\ boldsymbol {\ varphi}}} \\ + \ izquierda [{\ frac {\ parcial T _ {\ rho z}} {\ parcial \ rho}} + {\ frac {1} {\ rho}} {\ frac {\ parcial T _ {\ varphi z}} {\ parcial \ varphi}} + {\ frac {\ parcial T_ {zz}} {\ parcial z}} + {\ frac {T _ {\ rho z}} {\ rho}} \ derecha] & {\ hat {\ mathbf {z}}} \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3116bd7e75151c8d599b5e090d2433daffa21069)
![{\ Displaystyle {\ begin {alineado} \ left [{\ frac {\ parcial T_ {rr}} {\ parcial r}} + 2 {\ frac {T_ {rr}} {r}} + {\ frac {1 } {r}} {\ frac {\ parcial T _ {\ theta r}} {\ parcial \ theta}} + {\ frac {\ cot \ theta} {r}} T _ {\ theta r} + {\ frac { 1} {r \ sin \ theta}} {\ frac {\ parcial T _ {\ varphi r}} {\ parcial \ varphi}} - {\ frac {1} {r}} (T _ {\ theta \ theta} + T _ {\ varphi \ varphi}) \ right] & {\ hat {\ mathbf {r}}} \\ + \ left [{\ frac {\ parcial T_ {r \ theta}} {\ parcial r}} + 2 {\ frac {T_ {r \ theta}} {r}} + {\ frac {1} {r}} {\ frac {\ parcial T _ {\ theta \ theta}} {\ parcial \ theta}} + {\ frac {\ cot \ theta} {r}} T _ {\ theta \ theta} + {\ frac {1} {r \ sin \ theta}} {\ frac {\ parcial T _ {\ varphi \ theta}} {\ parcial \ varphi}} + {\ frac {T _ {\ theta r}} {r}} - {\ frac {\ cot \ theta} {r}} T _ {\ varphi \ varphi} \ right] & {\ hat {\ símbolo en negrita {\ theta}}} \\ + \ left [{\ frac {\ parcial T_ {r \ varphi}} {\ parcial r}} + 2 {\ frac {T_ {r \ varphi}} {r}} + {\ frac {1} {r}} {\ frac {\ parcial T _ {\ theta \ varphi}} {\ parcial \ theta}} + {\ frac {1} {r \ sin \ theta}} {\ frac { \ parcial T _ {\ varphi \ varphi}} {\ parcial \ varphi}} + {\ frac {T _ {\ var phi r}} {r}} + {\ frac {\ cot \ theta} {r}} (T _ {\ theta \ varphi} + T _ {\ varphi \ theta}) \ right] & {\ hat {\ boldsymbol { \ varphi}}} \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89522d9531233ee5f0a581ec441bb20c337a13b8)