Teorema de Stokes generalizado - Generalized Stokes theorem

En cálculo vectorial y geometría diferencial, el teorema de Stokes generalizado (a veces con apóstrofo como teorema de Stokes o teorema de Stokes ), también llamado teorema de Stokes-Cartan , es un enunciado sobre la integración de formas diferenciales en variedades , que simplifica y generaliza varios teoremas del cálculo vectorial . Es una generalización del teorema fundamental del cálculo de Isaac Newton que relaciona integrales de línea bidimensionales con integrales de superficie tridimensionales.

El teorema de Stokes dice que la integral de una forma diferencial $ω$ sobre el límite de alguna variedad orientable $Ω$ es igual a la integral de su derivada exterior $dω$ sobre la totalidad de $Ω$ , es decir,

{\ Displaystyle \ int _ {\ parcial \ Omega} \ omega = \ int _ {\ Omega} d \ omega \ ,.}

El teorema de Stokes fue formulado en su forma moderna por Élie Cartan en 1945, siguiendo un trabajo anterior sobre la generalización de los teoremas del cálculo vectorial de Vito Volterra , Édouard Goursat y Henri Poincaré .

Esta forma moderna del teorema de Stokes es una vasta generalización de un resultado clásico que Lord Kelvin le comunicó a George Stokes en una carta fechada el 2 de julio de 1850. Stokes estableció el teorema como una pregunta en el examen del Premio Smith de 1854 , que llevó al resultado que lleva su nombre. Fue publicado por primera vez por Hermann Hankel en 1861. Este teorema clásico de Kelvin-Stokes relaciona la integral de superficie del rizo de un campo vectorial $F$ sobre una superficie (es decir, el flujo del $rizo F$ ) en tres espacios euclidianos con la integral de línea del campo vectorial sobre su límite (también conocido como integral de bucle).

Ejemplo de análisis de vector clásico simple

Sea $γ : [a, b] \to R 2$ una curva plana de Jordan suave a trozos . El teorema de la curva de Jordan implica que $γ$ divide $R$ $2$ en dos componentes, uno compacto y otro no compacto. Sea $D$ la parte compacta que está limitada por $γ$ y suponga que $ψ$ $:$ $D$ $\to$ $R$ $3$ es suave, con $S$ $: =$ $ψ$ $($ $D$ $)$ . Si $Γ$ es la curva espacial definida por $Γ ($ $t$ $) =$ $ψ$ $($ $γ$ $($ $t$ $))$ y $F$ es un campo vectorial suave en $R$ $3$ , entonces:

{\ Displaystyle \ oint _ {\ Gamma} \ mathbf {F} \, \ cdot \, d {\ mathbf {\ Gamma}} = \ iint _ {S} \ nabla \ times \ mathbf {F} \, \ cdot \, d \ mathbf {S}}

Esta declaración clásica, es un caso especial de la formulación general mencionada anteriormente después de hacer una identificación del campo vectorial con una forma 1 y su rizo con una forma dos a través de

{\ displaystyle {\ begin {pmatrix} F_ {x} \\ F_ {y} \\ F_ {z} \\\ end {pmatrix}} \ cdot d \ Gamma \ to F_ {x} \, dx + F_ { y} \, dy + F_ {z} \, dz}

{\ Displaystyle \ nabla \ times {\ begin {pmatrix} F_ {x} \\ F_ {y} \\ F_ {z} \ end {pmatrix}} \ cdot d \ mathbf {S} = {\ begin {pmatrix} \ parcial _ {y} F_ {z} - \ parcial _ {z} F_ {y} \\\ parcial _ {z} F_ {x} - \ parcial _ {x} F_ {z} \\\ parcial _ { x} F_ {y} - \ parcial _ {y} F_ {x} \\\ end {pmatrix}} \ cdot d \ mathbf {S} \ to}

{\ Displaystyle d (F_ {x} \, dx + F_ {y} \, dy + F_ {z} \, dz) = (\ parcial _ {y} F_ {z} - \ parcial _ {z} F_ { y}) \, dy \ cuña dz + (\ parcial _ {z} F_ {x} - \ parcial _ {x} F_ {z}) \, dz \ cuña dx + (\ parcial _ {x} F_ {y} - \ parcial _ {y} F_ {x}) \, dx \ cuña dy}

.

Otras generalizaciones clásicas del teorema fundamental del cálculo como el teorema de la divergencia y el teorema de Green son casos especiales de la formulación general establecida anteriormente después de hacer una identificación estándar de campos vectoriales con formas diferenciales (diferentes para cada uno de los teoremas clásicos).

Introducción

El teorema fundamental del cálculo establece que la integral de una función $f$ en el intervalo $[a, b]$ se puede calcular encontrando una antiderivada $F$ de $f$ :

{\ Displaystyle \ int _ {a} ^ {b} f (x) \, dx = F (b) -F (a) \ ,.}

El teorema de Stokes es una amplia generalización de este teorema en el siguiente sentido.

Por la elección de $F$ , $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} dF/dx= F ( x )$ . En el lenguaje de las formas diferenciales , esto significa que $f (x) dx$ es la derivada exterior de la forma 0, es decir, la función $F$ : en otras palabras, que $dF = f dx$ . Los Stokes generales teorema se aplica a formas diferenciales más altas $omega$ en lugar de sólo 0-formas, tales como $F$ .
Un intervalo cerrado $[a, b]$ es un ejemplo simple de una variedad unidimensional con límite . Su límite es el conjunto que consiste en los dos puntos de $una$ y $b$ . La integración de $f$ en el intervalo puede generalizarse para integrar formas en una variedad de dimensiones superiores. Se necesitan dos condiciones técnicas: el colector debe ser orientable y la forma debe tener un soporte compacto para dar una integral bien definida.
Los dos puntos de $una$ y $b$ forman el límite del intervalo cerrado. De manera más general, el teorema de Stokes se aplica a variedades orientadas $M$ con límite. El límite $\partial M$ de $M$ es en sí mismo un colector y hereda una orientación natural de la de $M$ . Por ejemplo, la orientación natural del intervalo da una orientación de los dos puntos límite. Intuitivamente, $a$ hereda la orientación opuesta que $b$ , ya que están en extremos opuestos del intervalo. Entonces, "integrar" $F$ sobre dos puntos de frontera $a$ , $b$ es tomar la diferencia $F (b) - F (a)$ .

En términos aún más simples, se pueden considerar los puntos como límites de curvas, es decir, límites de dimensión 0 de variedades unidimensionales. Entonces, al igual que uno puede encontrar el valor de una integral ( $f dx = dF$ ) sobre una variedad unidimensional ( $[a, b]$ ) considerando la anti-derivada ( $F$ ) en los límites 0-dimensionales ( ${a, b$ }), se puede generalizar el teorema fundamental del cálculo, con algunas salvedades adicionales, para tratar el valor de integrales ( $dω$ ) sobre variedades $n-$ dimensionales ( $Ω$ ) considerando la antiderivada ( $ω$ ) en el $(n - 1 )$ -Límites dimensionales ( $\partialΩ$ ) de la variedad.

Entonces, el teorema fundamental dice:

{\ Displaystyle \ int _ {[a, b]} f (x) \, dx = \ int _ {[a, b]} \, dF = \ int _ {\ {a \} ^ {-} \ cup \ {b \} ^ {+}} F = F (b) -F (a) \ ,.}

Formulación para colectores lisos con límite

Sea $Ω$ una variedad suave orientada con un límite de dimensión $ny$ sea $α$ una forma $n$ - diferencial suave que se apoye de forma compacta en $Ω$ . Primero, suponga que $α$ está soportado de forma compacta en el dominio de un solo gráfico de coordenadas orientado ${$ $U$ $,$ $φ$ $}$ . En este caso, definimos la integral de $α$ sobre $Ω$ como

{\ Displaystyle \ int _ {\ Omega} \ alpha = \ int _ {\ varphi (U)} (\ varphi ^ {- 1}) ^ {*} \ alpha \ ,,}

es decir, mediante el retroceso de

α

a

R n

.

De manera más general, la integral de $α$ sobre $Ω$ se define de la siguiente manera: Sea ${ψ i}$ una partición de unidad asociada con una cobertura localmente finita ${$ $U$ $i$ $,$ $φ$ $i$ $}$ de gráficos de coordenadas (consistentemente orientados), luego defina la integral

{\ Displaystyle \ int _ {\ Omega} \ alpha \ equiv \ sum _ {i} \ int _ {U_ {i}} \ psi _ {i} \ alpha \ ,,}

donde cada término en la suma se evalúa tirando hacia atrás a

R n

como se describe anteriormente. Esta cantidad está bien definida; es decir, no depende de la elección de los gráficos de coordenadas ni de la partición de la unidad.

El teorema de Stokes generalizado dice:

Teorema ( Stokes-Cartan ) - Si es una suave - forma con soporte compacto en liso -dimensional colector con frontera , denota el límite de dada la orientación inducida, y es la relación de inclusión , a continuación, ${\ Displaystyle \ omega}$ ${\ Displaystyle (n-1)}$ ${\ Displaystyle n}$ ${\ Displaystyle \ Omega}$ ${\ Displaystyle \ parcial \ Omega}$ ${\ Displaystyle \ Omega}$ ${\ Displaystyle i: \ parcial \ Omega \ hookrightarrow \ Omega}$

{\ Displaystyle \ int _ {\ Omega} d \ omega = \ int _ {\ parcial \ Omega} i ^ {*} \ omega.}

Convencionalmente, se abrevia como , ya que la retirada de una forma diferencial por el mapa de la inclusión es simplemente su restricción a su dominio: . Aquí está la derivada exterior , que se define utilizando únicamente la estructura del colector. El lado derecho a veces se escribe para enfatizar el hecho de que el múltiple no tiene límite. (Este hecho también es una implicación del teorema de Stokes, ya que para una variedad de dimensiones suaves dada , la aplicación del teorema dos veces da para cualquier forma , lo que implica que ). El lado derecho de la ecuación se usa a menudo para formular leyes integrales ; el lado izquierdo conduce entonces a formulaciones diferenciales equivalentes (ver más abajo). ${\ estilo de texto \ int _ {\ parcial \ Omega} i ^ {*} \ omega}$ ${\ estilo de texto \ int _ {\ parcial \ Omega} \ omega}$ ${\ Displaystyle i ^ {*} \ omega = \ omega | _ {\ parcial \ Omega}}$ ${\ Displaystyle d}$ ${\ estilo de texto \ unción _ {\ parcial \ Omega} \ omega}$ ${\ Displaystyle (n-1)}$ ${\ Displaystyle \ parcial \ Omega}$ ${\ Displaystyle n}$ ${\ Displaystyle \ Omega}$ ${\ estilo de texto \ int _ {\ parcial (\ parcial \ Omega)} \ omega = \ int _ {\ Omega} d (d \ omega) = 0}$ ${\ Displaystyle (n-2)}$ ${\ Displaystyle \ omega}$ ${\ estilo de visualización \ parcial (\ parcial \ Omega) = \ conjunto vacío}$

El teorema se usa a menudo en situaciones en las que hay una subvariedad orientada incrustada de alguna variedad mayor, a menudo , en la que se define la forma . ${\ Displaystyle \ Omega}$ ${\ Displaystyle \ mathbf {R} ^ {k}}$ ${\ Displaystyle \ omega}$

Preliminares topológicos; integración sobre cadenas

Sea $M$ una variedad suave . A (liso) singular $k$ -simplex en $M$ se define como una transformación suave de la simplex estándar en $R k$ a $M$ . El grupo $C k (M, Z)$ de singular $k$ - cadenas en $M$ se define para ser el grupo abeliano libre sobre el conjunto de singulares $k$ -simplices en $M$ . Estos grupos, junto con el mapa de límites, $\partial$ , definen un complejo de cadenas . El grupo correspondiente homología (resp. Cohomology) es isomorfo a la usual singular homología grupo $H k (M, Z)$ (resp. El singular cohomology grupo $H k (M, Z)$ ), que se define usando continua en lugar de simplices suaves en $M$ .

Por otro lado, las formas diferenciales, con la derivada exterior, $d$ , como mapa de conexión, forman un complejo cocadena, que define los grupos de cohomología de De Rham $H k dR (M, R)$ .

Las formas $k$ diferenciales se pueden integrar sobre un $k-$ simple de forma natural, retrocediendo a $R k$ . Extender por linealidad le permite a uno integrarse sobre cadenas. Esto da un mapa lineal desde el espacio de $k-$ formas al $k-$ ésimo grupo de cadenas singulares, $C k (M, Z)$ , los funcionales lineales en $C k (M, Z)$ . En otras palabras, un $k$ -form $ω$ define un funcional

{\ Displaystyle I (\ omega) (c) = \ oint _ {c} \ omega.}

en las cadenas

k

. El teorema de Stokes dice que este es un mapa en cadena de la cohomología de Rham a la cohomología singular con coeficientes reales; la derivada exterior,

d

, se comporta como el dual de

\partial

en las formas. Esto da un homomorfismo de la cohomología de Rham a la cohomología singular. A nivel de formas, esto significa:

formas cerradas, es decir, $dω = 0$ , tienen integral cero sobre los límites , es decir, sobre variedades que se pueden escribir como $\partialΣ c M c$ , y
las formas exactas, es decir, $ω = dσ$ , tienen integral cero sobre ciclos , es decir, si los límites suman el conjunto vacío: $Σ c M c = \emptyset$ .

El teorema de De Rham muestra que este homomorfismo es de hecho un isomorfismo . Entonces, lo contrario a 1 y 2 anteriores es cierto. En otras palabras, si ${c i}$ son ciclos que generan el $k-$ ésimo grupo de homología, entonces para cualquier número real correspondiente, ${a i}$ , existe una forma cerrada, $ω$ , tal que

{\ Displaystyle \ oint _ {c_ {i}} \ omega = a_ {i} \ ,,}

y esta forma es única hasta formas exactas.

El teorema de Stokes sobre variedades suaves puede derivarse del teorema de Stokes para cadenas en variedades suaves y viceversa. Dicho formalmente, este último dice:

Teorema ( teorema de Stokes para las cadenas ) - Si $c$ es una cadena $k$ suave en una variedad suave $M$ , y $ω$ es una forma suave $(k - 1)$ en $M$ , entonces

{\ Displaystyle \ int _ {\ parcial c} \ omega = \ int _ {c} d \ omega.}

Principio subyacente

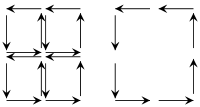
Para simplificar estos argumentos topológicos, vale la pena examinar el principio subyacente considerando un ejemplo para $d = 2$ dimensiones. La idea esencial se puede entender por el diagrama de la izquierda, que muestra que, en un mosaico orientado de un colector, los caminos interiores se recorren en direcciones opuestas; sus contribuciones a la integral de trayectoria se cancelan entre sí por pares. Como consecuencia, solo queda la contribución de la frontera. Por lo tanto, basta con probar el teorema de Stokes para teselaciones suficientemente finas (o, de manera equivalente, simples ), lo que generalmente no es difícil.

Generalización a conjuntos aproximados

Una región (aquí llamada

D en

lugar de

Ω

) con un límite suave a trozos. Este es un colector con esquinas , por lo que su límite no es un colector uniforme.

La formulación anterior, en la que $Ω$ es una variedad suave con límite, no es suficiente en muchas aplicaciones. Por ejemplo, si el dominio de integración se define como la región plana entre dos coordenadas $x$ y las gráficas de dos funciones, a menudo sucederá que el dominio tenga esquinas. En tal caso, los puntos de las esquinas significan que $Ω$ no es una variedad uniforme con límite, por lo que el enunciado del teorema de Stokes dado anteriormente no se aplica. No obstante, es posible comprobar que la conclusión del teorema de Stokes sigue siendo cierta. Esto se debe a que $Ω$ y su límite se comportan bien lejos de un pequeño conjunto de puntos (un conjunto de medidas cero ).

Whitney demostró una versión del teorema de Stokes que permite la aspereza. Suponga que $D$ es un subconjunto abierto acotado conectado de $R n$ . Llame a $D$ un dominio estándar si satisface la siguiente propiedad: Existe un subconjunto $P$ de $\partial D$ , abierto en $\partial D$ , cuyo complemento en $\partial D$ tiene Hausdorff $(n - 1)$ -medida cero; y tal que cada punto de $P$ tiene un vector normal generalizado . Este es un vector $v (x)$ tal que, si se elige un sistema de coordenadas de modo que $v (x)$ sea el primer vector base, entonces, en una vecindad abierta alrededor de $x$ , existe una función suave $f (x 2, .. ., x n)$ tal que $P$ es la gráfica ${x 1 = f (x 2, ..., x n)}$ y $D$ es la región ${x 1 : x 1 < f (x 2, ..., x n)}$ . Whitney observa que el límite de un dominio estándar es la unión de un conjunto de medida cero de Hausdorff $(n - 1)$ y una unión finita o contable de múltiples $(n - 1)$ -variedades suaves, cada una de las cuales tiene el dominio en solo una lado. Luego demuestra que si $D$ es un dominio estándar en $R n$ , $ω$ es una forma $(n - 1)$ que está definida, continua y limitada en $D \cup P$ , suave en $D$ , integrable en $P$ , y tal que $dω$ es integrable en $D$ , entonces se cumple el teorema de Stokes, es decir,

{\ Displaystyle \ int _ {P} \ omega = \ int _ {D} d \ omega \ ,.}

El estudio de las propiedades de la teoría de la medida de los conjuntos aproximados conduce a la teoría de la medida geométrica . Federer y Harrison han probado incluso versiones más generales del teorema de Stokes.

Casos especiales

La forma general del teorema de Stokes que usa formas diferenciales es más poderosa y más fácil de usar que los casos especiales. Las versiones tradicionales se pueden formular utilizando coordenadas cartesianas sin la maquinaria de la geometría diferencial y, por tanto, son más accesibles. Además, son mayores y, como resultado, sus nombres son más familiares. Las formas tradicionales a menudo son consideradas más convenientes por los científicos e ingenieros en ejercicio, pero la falta de naturalidad de la formulación tradicional se hace evidente cuando se utilizan otros sistemas de coordenadas, incluso los familiares, como las coordenadas esféricas o cilíndricas. Existe la posibilidad de confusión en la forma en que se aplican los nombres y el uso de formulaciones duales.

Teorema de Kelvin-Stokes

Una ilustración del teorema de Kelvin-Stokes, con superficie

Σ

, su límite

\partialΣ

y el vector "normal"

n

.

Este es un caso (dualizado) (1 + 1) -dimensional, para una forma 1 (dualizado porque es una declaración sobre campos vectoriales ). Este caso especial a menudo se denomina teorema de Stokes en muchos cursos universitarios de introducción al cálculo vectorial y se utiliza en física e ingeniería. También se lo conoce a veces como el teorema del rizo .

El teorema clásico de Kelvin-Stokes relaciona la integral de superficie del rizo de un campo vectorial sobre una superficie $Σ$ en tres espacios euclidianos con la integral de línea del campo vectorial sobre su límite. Es un caso especial del teorema general de Stokes (con $n = 2$ ) una vez que identificamos un campo vectorial con una forma 1 usando la métrica en el espacio euclidiano 3. La curva de la integral de línea, $\partialΣ$ , debe tener una orientación positiva , lo que significa que $\partialΣ$ apunta en sentido antihorario cuando la normal de la superficie , $n$ , apunta hacia el espectador.

Una consecuencia del teorema de Kelvin-Stokes es que las líneas de campo de un campo vectorial con curvatura cero no pueden ser contornos cerrados. La fórmula se puede reescribir como:

Teorema : suponga que $F = (P (x, y, z), Q (x, y, z), R (x, y, z))$ se define en una región con superficie lisa $Σ$ y tiene derivadas parciales continuas de primer orden . Luego

{\ Displaystyle {\ begin {alineado} & \ iint _ {\ Sigma} {\ Bigg (} \ left ({\ frac {\ parcial R} {\ parcial y}} - {\ frac {\ parcial Q} {\ parcial z}} \ derecha) \, dy \, dz + \ izquierda ({\ frac {\ parcial P} {\ parcial z}} - {\ frac {\ parcial R} {\ parcial x}} \ derecha) \, dz \, dx + \ izquierda ({\ frac {\ parcial Q} {\ parcial x}} - {\ frac {\ parcial P} {\ parcial y}} \ derecha) \, dx \, dy {\ Bigg)} \\ [4pt] = {} & \ oint _ {\ parcial \ Sigma} {\ Big (} P \, dx + Q \, dy + R \, dz {\ Big)} \ ,, \ end {alineado} }}

donde $P$ , $Q$ y $R$ son los componentes de $F$ , y $\partialΣ$ es el límite de la región $Σ$ .

Teorema de green

El teorema de Green es inmediatamente reconocible como el tercer integrando de ambos lados en la integral en términos de $P$ , $Q$ y $R$ antes citados.

En electromagnetismo

Dos de las cuatro ecuaciones de Maxwell involucran curvas de campos vectoriales 3-D, y sus formas diferencial e integral están relacionadas por el teorema de Kelvin-Stokes . Se debe tener cuidado para evitar casos con límites móviles: las derivadas de tiempo parcial están destinadas a excluir tales casos. Si se incluyen límites móviles, el intercambio de integración y diferenciación introduce términos relacionados con el movimiento de límites no incluidos en los resultados a continuación (consulte Diferenciación bajo el signo integral ):

Nombre	Forma diferencial	Forma integral (usando el teorema de Kelvin-Stokes más invariancia relativista, $\int \partial / \partial t ... \to D / dt \int ...$ )
Ecuación de Maxwell-Faraday Ley de inducción de Faraday :	${\ Displaystyle \ quad \ nabla \ times \ mathbf {E} = - {\ frac {\ parcial \ mathbf {B}} {\ parcial t}} \ quad}$	${\ Displaystyle {\ begin {alineado} \ quad \ oint _ {C} \ mathbf {E} \ cdot d \ mathbf {l} & = \ iint _ {S} \ nabla \ times \ mathbf {E} \ cdot d \ mathbf {A} \\ & = - \ iint _ {S} {\ frac {\ parcial \ mathbf {B}} {\ parcial t}} \ cdot d \ mathbf {A} \ end {alineado}} \ quad }$ (con $C$ y $S$ no necesariamente estacionarios)
Ley de Ampère (con extensión de Maxwell):	${\ Displaystyle \ quad \ nabla \ times \ mathbf {H} = \ mathbf {J} + {\ frac {\ parcial \ mathbf {D}} {\ parcial t}} \ quad}$	${\ Displaystyle {\ begin {alineado} \ quad \ oint _ {C} \ mathbf {H} \ cdot d \ mathbf {l} & = \ iint _ {S} \ nabla \ times \ mathbf {H} \ cdot d \ mathbf {A} \\ & = \ iint _ {S} \ mathbf {J} \ cdot d \ mathbf {A} + \ iint _ {S} {\ frac {\ parcial \ mathbf {D}} {\ parcial t}} \ cdot d \ mathbf {A} \ end {alineado}} \ quad}$ (con $C$ y $S$ no necesariamente estacionarios)

El subconjunto de ecuaciones de Maxwell enumerado anteriormente es válido para campos electromagnéticos expresados en unidades SI . En otros sistemas de unidades, como CGS o unidades gaussianas , los factores de escala para los términos difieren. Por ejemplo, en unidades gaussianas, la ley de inducción de Faraday y la ley de Ampère toman las formas:

{\ Displaystyle {\ begin {alineado} \ nabla \ times \ mathbf {E} & = - {\ frac {1} {c}} {\ frac {\ parcial \ mathbf {B}} {\ parcial t}} \ ,, \\\ nabla \ veces \ mathbf {H} & = {\ frac {1} {c}} {\ frac {\ parcial \ mathbf {D}} {\ parcial t}} + {\ frac {4 \ pi} {c}} \ mathbf {J} \ ,, \ end {alineado}}}

respectivamente, donde $c$ es la velocidad de la luz en el vacío.

Teorema de divergencia

Asimismo, el teorema de la divergencia

{\ Displaystyle \ int _ {\ mathrm {Vol}} \ nabla \ cdot \ mathbf {F} \, d _ {\ mathrm {Vol}} = \ oint _ {\ partial \ operatorname {Vol}} \ mathbf {F} \ cdot d {\ boldsymbol {\ Sigma}}}

Es un caso especial si identificamos un campo vectorial con la forma $(n - 1)$ obtenida al contraer el campo vectorial con la forma de volumen euclidiana. Una aplicación de esto es el caso $F = f c$ donde $c$ es un vector constante arbitrario. Resolver la divergencia del producto da

{\ Displaystyle \ mathbf {c} \ cdot \ int _ {\ mathrm {Vol}} \ nabla f \, d _ {\ mathrm {Vol}} = \ mathbf {c} \ cdot \ oint _ {\ partial \ mathrm { Vol}} f \, d {\ boldsymbol {\ Sigma}} \ ,.}

Dado que esto es válido para todo $c$ , encontramos

{\ Displaystyle \ int _ {\ mathrm {Vol}} \ nabla f \, d _ {\ mathrm {Vol}} = \ oint _ {\ partial \ mathrm {Vol}} f \, d {\ boldsymbol {\ Sigma} } \ ,.}

Ver también

Lema de Chandrasekhar-Wentzel

Notas al pie

Referencias

Otras lecturas

Grunsky, Helmut (1983). El teorema del general Stokes . Boston: Pitman. ISBN 0-273-08510-7.
Katz, Victor J. (mayo de 1979). "La historia del teorema de Stokes". Revista de Matemáticas . 52 (3): 146-156. doi : 10.2307 / 2690275 . JSTOR 2690275 .
Loomis, Lynn Harold ; Sternberg, Shlomo (2014). Cálculo avanzado . Hackensack, Nueva Jersey: World Scientific. ISBN 978-981-4583-93-0.
Madsen, Ib ; Tornehave, Jørgen (1997). Del cálculo a la cohomología: cohomología de De Rham y clases características . Cambridge, Reino Unido: Cambridge University Press. ISBN 0-521-58956-8.
Marsden, Jerrold E .; Anthony, Tromba (2003). Cálculo vectorial (5ª ed.). W. H. Freeman.
Lee, John (2003). Introducción a los colectores lisos . Springer-Verlag. ISBN 978-0-387-95448-6.
Rudin, Walter (1976). Principios del análisis matemático . Nueva York, NY: McGraw – Hill. ISBN 0-07-054235-X.
Spivak, Michael (1965). Cálculo en colectores: un enfoque moderno de los teoremas clásicos del cálculo avanzado . San Francisco: Benjamin Cummings. ISBN 0-8053-9021-9.
Stewart, James (2009). Cálculo: conceptos y contextos . Aprendizaje Cengage. págs. 960–967. ISBN 978-0-495-55742-5.
Stewart, James (2003). Cálculo: Funciones trascendentales tempranas (5ª ed.). Brooks / Cole.
Tu, Loring W. (2011). Una introducción a los colectores (2ª ed.). Nueva York: Springer. ISBN 978-1-4419-7399-3.

enlaces externos

Medios relacionados con el teorema de Stokes en Wikimedia Commons
"Fórmula de Stokes" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
Prueba del teorema de la divergencia y el teorema de Stokes
Cálculo 3 - Teorema de Stokes de lamar.edu - una explicación expositiva
"Teorema de Stokes sobre colectores" . Aleph Zero . 3 de mayo de 2020 - a través de YouTube .

Languages

In other projects