Homología singular - Singular homology

En topología algebraica , la homología singular se refiere al estudio de un determinado conjunto de invariantes algebraicos de un espacio topológico X , los llamados grupos de homología. Intuitivamente, la homología singular cuenta, para cada dimensión n , los huecos n- dimensionales de un espacio. La homología singular es un ejemplo particular de una teoría de homología , que ahora se ha convertido en una colección bastante amplia de teorías. De las diversas teorías, quizás sea una de las más sencillas de entender, ya que está construida sobre construcciones bastante concretas. ${\ Displaystyle H_ {n} (X).}$

En resumen, la homología singular se construye tomando mapas del estándar n- simple en un espacio topológico y componiéndolos en sumas formales , llamadas cadenas singulares . La operación de límite, mapeando cada n -simplex dimensional a su límite ( n −1) -dimensional , induce el complejo de cadena singular . La homología singular es entonces la homología del complejo de cadena. Los grupos de homología resultantes son los mismos para todos los espacios equivalentes de homotopía , que es la razón de su estudio. Estas construcciones se pueden aplicar a todos los espacios topológicos, por lo que la homología singular se puede expresar en términos de teoría de categorías , donde la homología se puede expresar como un funtor de la categoría de espacios topológicos a la categoría de grupos abelianos graduados .

Simplices singulares

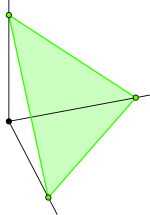
Un n- simplex singular en un espacio topológico X es una función continua (también llamada mapa) del estándar n - simplex a X , escrito Este mapa no necesita ser inyectivo , y puede haber simples simples no equivalentes con la misma imagen en X . ${\ Displaystyle \ sigma}$ ${\ Displaystyle \ Delta ^ {n}}$${\ Displaystyle \ sigma: \ Delta ^ {n} \ to X.}$

El límite de denotado como se define como la suma formal de los singulares ( n  - 1) -simplices representados por la restricción de a las caras del estándar n -simplex, con un signo alterno para tener en cuenta la orientación. (Una suma formal es un elemento del grupo abeliano libre en los simples. La base del grupo es el conjunto infinito de todos los posibles singulares simples. La operación de grupo es "suma" y la suma de simplex a con simplex b suele ser simplemente designado a  +  b , pero a  +  a  = 2 a y así sucesivamente. Todo simplex a tiene un negativo - a .) Por lo tanto, si designamos por sus vértices ${\ Displaystyle \ sigma,}$${\ estilo de visualización \ parcial _ {n} \ sigma,}$${\ Displaystyle \ sigma}$${\ Displaystyle \ sigma}$

${\ Displaystyle [p_ {0}, p_ {1}, \ ldots, p_ {n}] = [\ sigma (e_ {0}), \ sigma (e_ {1}), \ ldots, \ sigma (e_ { norte})]}$

correspondiente a los vértices del n- simplex estándar (que por supuesto no especifica completamente el simplex singular producido por ), entonces ${\ Displaystyle e_ {k}}$${\ Displaystyle \ Delta ^ {n}}$${\ Displaystyle \ sigma}$

${\ Displaystyle \ partial _ {n} \ sigma = \ sum _ {k = 0} ^ {n} (- 1) ^ {k} \ sigma \ mid _ {[p_ {0}, \ ldots, p_ {k -1}, p_ {k + 1}, \ ldots, p_ {n}]}}$

es una suma formal de las caras de la imagen simplex designadas de una manera específica. (Es decir, una cara en particular tiene que ser la restricción de a una cara de la cual depende del orden en que se enumeran sus vértices). Así, por ejemplo, el límite de (una curva que va de a ) es la suma formal (o "diferencia formal") . ${\ Displaystyle \ sigma}$${\ Displaystyle \ Delta ^ {n}}$${\ Displaystyle \ sigma = [p_ {0}, p_ {1}]}$${\ Displaystyle p_ {0}}$${\ Displaystyle p_ {1}}$${\ Displaystyle [p_ {1}] - [p_ {0}]}$

Complejo de cadena singular

La construcción habitual de homología singular procede definiendo sumas formales de simples, que pueden entenderse como elementos de un grupo abeliano libre , y luego muestra que podemos definir un cierto grupo, el grupo de homología del espacio topológico, que involucra al operador de frontera. .

Consideremos en primer lugar el conjunto de todos los posibles singular n -simplices en un espacio topológico X . Este conjunto se puede utilizar como base de un grupo abeliano libre , de modo que cada n- simple singular es un generador del grupo. Por supuesto, este conjunto de generadores suele ser infinito, con frecuencia incontable , ya que hay muchas formas de mapear un simplex en un espacio topológico típico. El grupo abeliano libre generado por esta base se denomina comúnmente . Los elementos de se denominan n- cadenas singulares ; son sumas formales de simples simples con coeficientes enteros. ${\ Displaystyle \ sigma _ {n} (X)}$${\ Displaystyle C_ {n} (X)}$${\ Displaystyle C_ {n} (X)}$

El límite se extiende fácilmente para actuar sobre n cadenas singulares . La extensión, denominada operador de límites , escrita como ${\ estilo de visualización \ parcial}$

${\ estilo de visualización \ parcial _ {n}: C_ {n} \ a C_ {n-1},}$

es un homomorfismo de grupos. El operador de límite, junto con el , forman un complejo en cadena de grupos abelianos, llamado complejo singular . A menudo se denota como o más simplemente . ${\ Displaystyle C_ {n}}$${\ Displaystyle (C _ {\ bullet} (X), \ partial _ {\ bullet})}$${\ Displaystyle C _ {\ bullet} (X)}$

El núcleo del operador de límite es , y se denomina grupo de n ciclos singulares . La imagen del operador de límites es , y se denomina grupo de n- límites singulares . ${\ Displaystyle Z_ {n} (X) = \ ker (\ parcial _ {n})}$${\ Displaystyle B_ {n} (X) = \ operatorname {im} (\ partial _ {n + 1})}$

También se puede demostrar que . El -ésimo grupo de homología de se define entonces como el grupo de factores${\ estilo de visualización \ parcial _ {n} \ circ \ parcial _ {n + 1} = 0}$${\ Displaystyle n}$${\ Displaystyle X}$

${\ Displaystyle H_ {n} (X) = Z_ {n} (X) / B_ {n} (X).}$

Los elementos de se denominan clases de homología . ${\ Displaystyle H_ {n} (X)}$

Invariancia de homotopía

Si X e Y son dos espacios topológicos con el mismo tipo de homotopía (es decir, son equivalentes de homotopía ), entonces

${\ Displaystyle H_ {n} (X) \ cong H_ {n} (Y) \,}$

para todo n ≥ 0. Esto significa que los grupos de homología son invariantes topológicos .

En particular, si X es un espacio contráctil conectado , entonces todos sus grupos de homología son 0, excepto . ${\ Displaystyle H_ {0} (X) \ cong \ mathbb {Z}}$

Una prueba de la invariancia de homotopía de grupos de homología singulares se puede esbozar como sigue. Un mapa continuo f : X → Y induce un homomorfismo

${\ Displaystyle f _ {\ sharp}: C_ {n} (X) \ rightarrow C_ {n} (Y).}$

Se puede verificar inmediatamente que

${\ Displaystyle \ parcial f _ {\ sostenido} = f _ {\ sostenido} \ parcial,}$

es decir, f _# es un mapa de cadena , que desciende a homomorfismos en homología

${\ Displaystyle f _ {*}: H_ {n} (X) \ rightarrow H_ {n} (Y).}$

Ahora mostramos que si f y g son homotópicamente equivalentes, entonces f _* = g _* . De esto se deduce que si f es una equivalencia de homotopía, entonces f _* es un isomorfismo.

Sea F  : X × [0, 1] → Y una homotopía que toma f a g . A nivel de cadenas, defina un homomorfismo

${\ Displaystyle P: C_ {n} (X) \ rightarrow C_ {n + 1} (Y)}$

que, geométricamente hablando, toma un σ elemento base: Δ ⁿ → X de C _n ( X ) a la "prisma" P (σ): Δ ⁿ × I → Y . El límite de P (σ) se puede expresar como

${\ estilo de visualización \ P parcial (\ sigma) = f _ {\ sostenido} (\ sigma) -g _ {\ agudo} (\ sigma) -P (\ parcial \ sigma).}$

Entonces, si α en C _n ( X ) es un ciclo n , entonces f _# ( α ) y g _# ( α ) difieren por un límite:

${\ Displaystyle f _ {\ sharp} (\ alpha) -g _ {\ sharp} (\ alpha) = \ parcial P (\ alpha),}$

es decir, son homólogos. Esto prueba la afirmación.

Functorialidad

La construcción anterior se puede definir para cualquier espacio topológico y se conserva mediante la acción de mapas continuos. Esta generalidad implica que la teoría de la homología singular puede reformularse en el lenguaje de la teoría de categorías . En particular, puede entenderse que el grupo de homología es un funtor desde la categoría de espacios topológicos Top hasta la categoría de grupos abelianos Ab .

Considere primero que es un mapa de espacios topológicos a grupos abelianos libres. Esto sugiere que podría tomarse como un funtor, siempre que se pueda comprender su acción sobre los morfismos de Top . Ahora bien, los morfismos de Top son funciones continuas, por lo que si es un mapa continuo de espacios topológicos, se puede extender a un homomorfismo de grupos. ${\ Displaystyle X \ mapsto C_ {n} (X)}$${\ Displaystyle C_ {n} (X)}$${\ Displaystyle f: X \ to Y}$

${\ Displaystyle f _ {*}: C_ {n} (X) \ a C_ {n} (Y) \,}$

definiendo

${\ Displaystyle f _ {*} \ left (\ sum _ {i} a_ {i} \ sigma _ {i} \ right) = \ sum _ {i} a_ {i} (f \ circ \ sigma _ {i} )}$

donde es un simplex singular y es una cadena n singular , es decir, un elemento de . Esto demuestra que es un functor ${\ Displaystyle \ sigma _ {i}: \ Delta ^ {n} \ to X}$${\ Displaystyle \ sum _ {i} a_ {i} \ sigma _ {i} \,}$${\ Displaystyle C_ {n} (X)}$${\ Displaystyle C_ {n}}$

${\ Displaystyle C_ {n}: \ mathbf {Arriba} \ a \ mathbf {Ab}}$

de la categoría de espacios topológicos a la categoría de grupos abelianos .

El operador de límites conmuta con mapas continuos, de modo que . Esto permite que todo el complejo de la cadena se trate como un funtor. En particular, esto muestra que el mapa es un functor${\ estilo de visualización \ parcial _ {n} f _ {*} = f _ {*} \ parcial _ {n}}$${\ Displaystyle X \ mapsto H_ {n} (X)}$

${\ Displaystyle H_ {n}: \ mathbf {Arriba} \ a \ mathbf {Ab}}$

de la categoría de espacios topológicos a la categoría de grupos abelianos. Por el axioma de homotopía, se tiene que también es un funtor, llamado functor de homología, que actúa sobre hTop , la categoría de homotopía del cociente : ${\ Displaystyle H_ {n}}$

${\ Displaystyle H_ {n}: \ mathbf {hTop} \ to \ mathbf {Ab}.}$

Esto distingue la homología singular de otras teorías de homología, en las que sigue siendo un funtor, pero no está necesariamente definido en todo Top . En cierto sentido, la homología singular es la teoría de homología "más grande", en el sentido de que cada teoría de homología en una subcategoría de Top concuerda con la homología singular en esa subcategoría. Por otro lado, la homología singular no tiene las propiedades categóricas más limpias; tal limpieza motiva el desarrollo de otras teorías de homología como la homología celular . ${\ Displaystyle H_ {n}}$

De manera más general, el functor de homología se define axiomáticamente, como un funtor en una categoría abeliana o, alternativamente, como un funtor en complejos de cadena , satisfaciendo axiomas que requieren un morfismo límite que convierte secuencias exactas cortas en secuencias exactas largas . En el caso de la homología singular, el functor de homología se puede factorizar en dos piezas, una pieza topológica y una pieza algebraica. La pieza topológica viene dada por

${\ Displaystyle C _ {\ bullet}: \ mathbf {Arriba} \ a \ mathbf {Comp}}$

que mapea espacios topológicos como y funciones continuas como . Aquí, entonces, se entiende que es el functor de cadena singular, que mapea los espacios topológicos a la categoría de complejos de cadena Comp (o Kom ). La categoría de complejos de cadenas tiene complejos de cadenas como objetos y mapas de cadenas como morfismos . ${\ Displaystyle X \ mapsto (C _ {\ bullet} (X), \ partial _ {\ bullet})}$${\ Displaystyle f \ mapsto f _ {*}}$${\ Displaystyle C _ {\ bullet}}$

La segunda parte algebraica es el functor de homología

${\ Displaystyle H_ {n}: \ mathbf {Comp} \ to \ mathbf {Ab}}$

que mapas

${\ Displaystyle C _ {\ bullet} \ mapsto H_ {n} (C _ {\ bullet}) = Z_ {n} (C _ {\ bullet}) / B_ {n} (C _ {\ bullet})}$

y lleva mapas de cadenas a mapas de grupos abelianos. Es este functor de homología el que puede definirse axiomáticamente, de modo que se erige por sí solo como un funtor en la categoría de complejos de cadena.

Los mapas de homotopía vuelven a entrar en la imagen definiendo mapas de cadena homotópicamente equivalentes. Por tanto, se puede definir la categoría de cociente hComp o K , la categoría de homotopía de complejos de cadena .

Coeficientes en R

Dado cualquier anillo unital R , el conjunto de n -simplices singulares en un espacio topológico puede tomarse como generadores de un R -módulo libre . Es decir, en lugar de realizar las construcciones anteriores desde el punto de partida de los grupos abelianos libres, se utilizan módulos R libres en su lugar. Todas las construcciones se llevan a cabo con poco o ningún cambio. El resultado de esto es

${\ Displaystyle H_ {n} (X, R) \}$

que ahora es un R -módulo . Por supuesto, no suele ser un módulo gratuito. El grupo de homología habitual se recupera al señalar que

${\ Displaystyle H_ {n} (X, \ mathbb {Z}) = H_ {n} (X)}$

cuando uno toma el anillo como el anillo de los enteros. La notación H _n ( X , R ) no debe confundirse con la notación casi idéntica H _n ( X , A ), que denota la homología relativa (a continuación).

Homología relativa

Para un subespacio , se entiende que la homología relativa H _n ( X , A ) es la homología del cociente de los complejos de cadena, es decir, ${\ Displaystyle A \ subconjunto X}$

${\ Displaystyle H_ {n} (X, A) = H_ {n} (C _ {\ bullet} (X) / C _ {\ bullet} (A))}$

donde el cociente de los complejos de cadenas viene dado por la secuencia exacta corta

${\ Displaystyle 0 \ to C _ {\ bullet} (A) \ to C _ {\ bullet} (X) \ to C _ {\ bullet} (X) / C _ {\ bullet} (A) \ to 0.}$

Cohomología

Al dualizar el complejo de cadena de homología (es decir, aplicando el functor Hom (-, R ), siendo R cualquier anillo) obtenemos un complejo de cocadena con mapa de límites . Los grupos de cohomología de X se definen como los grupos de homología de este complejo; en una broma, "la cohomología es la homología del co [el complejo dual]". ${\ Displaystyle \ delta}$

Los grupos de cohomología tienen una estructura algebraica más rica, o al menos más familiar, que los grupos de homología. En primer lugar, forman un álgebra graduada diferencial de la siguiente manera:

• el conjunto graduadas de grupos formar una graduada R - módulo ;
• Esto se puede dar la estructura de una graduada R - álgebra usando el producto de taza ;
• el homomorfismo de Bockstein β da un diferencial.

Hay operaciones de cohomología adicionales , y el álgebra de cohomología tiene estructura de adición mod p (como antes, la cohomología mod p es la cohomología del complejo de cocadena mod p , no la reducción mod p de la cohomología), en particular la estructura del álgebra de Steenrod .

Homología y cohomología de Betti

Dado que el número de teorías de homología se ha vuelto grande (ver Categoría: Teoría de homología ), los términos homología de Betti y cohomología de Betti se aplican a veces (particularmente por autores que escriben sobre geometría algebraica ) a la teoría singular, ya que dan lugar a los números de Betti de la espacios más familiares como los complejos simpliciales y las variedades cerradas .

Homología extraordinaria

Si uno define una teoría de homología axiomáticamente (a través de los axiomas de Eilenberg-Steenrod ), y luego relaja uno de los axiomas (el axioma de dimensión ), se obtiene una teoría generalizada, llamada teoría de homología extraordinaria . Estos surgieron originalmente en la forma de las teorías de cohomología extraordinarias , a saber, K-teoría y teoría cobordism . En este contexto, la homología singular se denomina homología ordinaria.

Ver también

• Categoría derivada
• Teorema de escisión
• Teorema de Hurewicz
• Homología simplicial
• Homología celular

Referencias

• Allen Hatcher, topología algebraica. Cambridge University Press, ISBN  0-521-79160-X e ISBN  0-521-79540-0
• JP May, Un curso conciso en topología algebraica , Chicago University Press ISBN  0-226-51183-9
• Joseph J. Rotman, Introducción a la topología algebraica , Springer-Verlag, ISBN  0-387-96678-1