Complejo de cadena - Chain complex

En matemáticas , un complejo de cadena es una estructura algebraica que consta de una secuencia de grupos (o módulos ) abelianos y una secuencia de homomorfismos entre grupos consecutivos de manera que la imagen de cada homomorfismo se incluye en el núcleo del siguiente. Asociado a un complejo de cadena está su homología , que describe cómo se incluyen las imágenes en los núcleos.

Un complejo de cocadena es similar a un complejo de cadena, excepto que sus homomorfismos siguen una convención diferente. La homología de un complejo cocadena se denomina cohomología.

En topología algebraica , el complejo de cadena singular de un espacio topológico X se construye usando mapas continuos desde un simplex a X, y los homomorfismos del complejo de cadena capturan cómo estos mapas se restringen al límite del símplex. La homología de este complejo de cadena se denomina homología singular de X y es un invariante de uso común de un espacio topológico.

Los complejos de cadenas se estudian en álgebra homológica , pero se utilizan en varias áreas de las matemáticas, como el álgebra abstracta , la teoría de Galois , la geometría diferencial y la geometría algebraica . Pueden definirse de manera más general en categorías abelianas .

Definiciones

Un complejo de cadena es una secuencia de grupos o módulos abelianos ..., A ₀ , A ₁ , A ₂ , A ₃ , A ₄ , ... conectados por homomorfismos (llamados operadores de frontera o diferenciales ) d _n : A _n → A _n₋₁ , de modo que la composición de dos mapas consecutivos cualesquiera sea el mapa cero. Explícitamente, los diferenciales satisfacen d _n ∘ d _n₊₁ = 0 , o con índices suprimidos, d ² = 0 . El complejo se puede escribir de la siguiente manera. ${\ Displaystyle (A _ {\ bullet}, d _ {\ bullet})}$

{\ displaystyle \ cdots {\ xleftarrow {d_ {0}}} A_ {0} {\ xleftarrow {d_ {1}}} A_ {1} {\ xleftarrow {d_ {2}}} A_ {2} {\ xleftarrow {d_ {3}}} A_ {3} {\ xleftarrow {d_ {4}}} A_ {4} {\ xleftarrow {d_ {5}}} \ cdots}

El complejo cocadena es la noción dual de un complejo en cadena. Consiste en una secuencia de grupos o módulos abelianos ..., A ⁰ , A ¹ , A ² , A ³ , A ⁴ , ... conectados por homomorfismos d ⁿ : A ⁿ → A ⁿ⁺¹ satisfaciendo d ⁿ⁺¹ ∘ d ⁿ = 0 . El complejo de cadenas conjuntas puede escribirse de forma similar al complejo de cadenas. ${\ Displaystyle (A ^ {\ bullet}, d ^ {\ bullet})}$

{\ displaystyle \ cdots {\ xrightarrow {d ^ {- 1}}} A ^ {0} {\ xrightarrow {d ^ {0}}} A ^ {1} {\ xrightarrow {d ^ {1}}} A ^ {2} {\ xrightarrow {d ^ {2}}} A ^ {3} {\ xrightarrow {d ^ {3}}} A ^ {4} {\ xrightarrow {d ^ {4}}} \ cdots}

El índice n en A _n o A ⁿ se denomina grado (o dimensión ). La diferencia entre los complejos de cadena y cocadena es que, en los complejos de cadena, los diferenciales disminuyen la dimensión, mientras que en los complejos de cocadena aumentan la dimensión. Todos los conceptos y definiciones de los complejos de cadena se aplican a los complejos de cocadena, excepto que seguirán esta convención diferente para la dimensión, y a menudo los términos recibirán el prefijo co- . En este artículo, se darán definiciones para complejos de cadenas cuando no se requiera la distinción.

Un complejo de cadena acotada es aquel en el que casi todos los A _n son 0; es decir, un complejo finito extendido hacia la izquierda y hacia la derecha en 0. Un ejemplo es el complejo de cadena que define la homología simplicial de un complejo simplicial finito . Un complejo de cadena está acotado por encima si todos los módulos por encima de algún grado fijo N son 0, y está acotado por debajo si todos los módulos por debajo de algún grado fijo son 0. Claramente, un complejo está acotado tanto por encima como por debajo si y solo si el complejo está acotado.

Los elementos de los grupos individuales de un complejo de (co) cadenas se denominan (co) cadenas . Los elementos del núcleo de d se denominan (co) ciclos (o elementos cerrados ) y los elementos de la imagen de d se denominan (co) límites (o elementos exactos ). Desde la definición del diferencial, todos los límites son ciclos. El n -ésimo grupo de (co) homología H _n ( H ⁿ ) es el grupo de (co) ciclos módulo (co) límites en grado n , es decir,

{\ Displaystyle H_ {n} = {\ frac {\ ker d_ {n}} {{\ mbox {im}} d_ {n + 1}}} \ quad \ left (H ^ {n} = {\ frac { \ ker d ^ {n}} {{\ mbox {im}} d ^ {n-1}}} \ right)}

Secuencias exactas

Una secuencia exacta (o complejo exacto ) es un complejo de cadena cuyos grupos de homología son todos cero. Esto significa que todos los elementos cerrados del complejo son exactos. Una secuencia exacta corta es una secuencia exacta limitada en la que solo los grupos A _k , A _{k +1} , A _{k +2} pueden ser distintos de cero. Por ejemplo, el siguiente complejo de cadena es una secuencia corta y exacta.

{\ displaystyle \ cdots {\ xrightarrow {}} \; 0 \; {\ xrightarrow {}} \; \ mathbf {Z} \; {\ xrightarrow {\ times p}} \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / p \ mathbf {Z} \; {\ xrightarrow {}} \; 0 \; {\ xrightarrow {}} \ cdots}

En el grupo intermedio, los elementos cerrados son los elementos p Z ; estos son claramente los elementos exactos de este grupo.

Mapas de cadena

Un mapa de cadena f entre dos complejos de cadena y es una secuencia de homomorfismos para cada n que conmuta con los operadores de límite en los dos complejos de cadena, entonces . Esto está escrito en el siguiente diagrama conmutativo . ${\ Displaystyle (A _ {\ bullet}, d_ {A, \ bullet})}$ ${\ Displaystyle (B _ {\ bullet}, d_ {B, \ bullet})}$ ${\ Displaystyle f _ {\ bullet}}$ ${\ Displaystyle f_ {n}: A_ {n} \ rightarrow B_ {n}}$ ${\ Displaystyle d_ {B, n} \ circ f_ {n} = f_ {n-1} \ circ d_ {A, n}}$

Un mapa de cadena envía ciclos a ciclos y límites a límites y, por lo tanto, induce un mapa de homología . ${\ Displaystyle (f _ {\ bullet}) _ {*}: H _ {\ bullet} (A _ {\ bullet}, d_ {A, \ bullet}) \ rightarrow H _ {\ bullet} (B _ {\ bullet}, d_ {B, \ bullet})}$

Un mapa continuo f entre los espacios topológicos X e Y induce un mapa de cadena entre los complejos de cadenas singulares de X e Y , y por lo tanto induce un mapa f _* entre la homología singular de X e Y también. Cuando X e Y son ambos iguales a la n -esfera , el mapa inducido por homología define el grado del mapa f .

El concepto de mapa de cadenas se reduce al de límite mediante la construcción del cono de un mapa de cadenas.

Homotopía en cadena

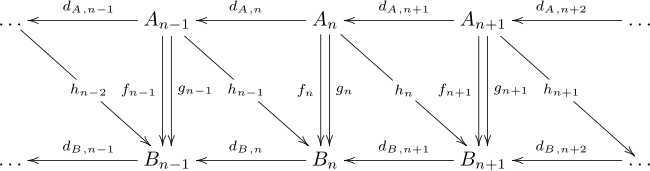
Una homotopía en cadena ofrece una forma de relacionar dos mapas de cadena que inducen el mismo mapa en grupos de homología, aunque los mapas pueden ser diferentes. Dados dos complejos de cadena A y B , y dos mapas de cadena f , g : A → B , una homotopía de cadena es una secuencia de homomorfismos h _n : A _n → B _{n +1} tal que hd _A + d _B h = f - g . Los mapas se pueden escribir en un diagrama de la siguiente manera, pero este diagrama no es conmutativo.

El mapa hd _A + d _B h se verifica fácilmente para inducir el mapa cero en la homología, para cualquier h . De ello se deduce inmediatamente que f y g inducir el mismo mapa en la homología. Se dice que f y g son homotópicos en cadena (o simplemente homotópicos ), y esta propiedad define una relación de equivalencia entre mapas de cadenas.

Sean X e Y espacios topológicos. En el caso de la homología singular, una homotopía entre mapas continuos f , g : X → Y induce una homotopía de cadena entre los mapas de cadena correspondientes af y g . Esto muestra que dos mapas homotópicos inducen el mismo mapa en homología singular. El nombre "homotopía en cadena" está motivado por este ejemplo.

Ejemplos

Homología singular

Sea X un espacio topológico. Defina C _n ( X ) para que n natural sea el grupo abeliano libre generado formalmente por n-simplices singulares en X , y defina el mapa de límites como ${\ estilo de visualización \ parcial _ {n}: C_ {n} (X) \ a C_ {n-1} (X)}$

{\ Displaystyle \ partial _ {n}: \, (\ sigma: [v_ {0}, \ ldots, v_ {n}] \ to X) \ mapsto \ sum _ {i = 0} ^ {n} (- 1) ^ {i} (\ sigma: [v_ {0}, \ ldots, {\ hat {v}} _ {i}, \ ldots, v_ {n}] \ to X)}

donde el sombrero denota la omisión de un vértice . Es decir, el límite de un simplex singular es la suma alterna de restricciones a sus caras. Se puede demostrar que ∂ ² = 0, por lo que es un complejo de cadena; la homología singular es la homología de este complejo. ${\ Displaystyle (C _ {\ bullet}, \ parcial _ {\ bullet})}$ ${\ Displaystyle H _ {\ bullet} (X)}$

La homología singular es una invariante útil de los espacios topológicos hasta la equivalencia de homotopía . El grupo de homología de cero grados es un grupo abeliano libre en los de caminos componentes de X .

cohomología de Rham

El diferencial k -formas en cualquier múltiple liso M forma un verdadero espacio de vector llamado Ω ^k ( M ) bajo adición. La derivada exterior d mapea Ω ^k ( M ) a Ω ^{k +1} ( M ), y d ² = 0 se sigue esencialmente de la simetría de las segundas derivadas , por lo que los espacios vectoriales de las formas k junto con la derivada exterior son un complejo cocadena.

{\ Displaystyle \ Omega ^ {0} (M) \ {\ stackrel {d} {\ to}} \ \ Omega ^ {1} (M) \ to \ Omega ^ {2} (M) \ to \ Omega ^ {3} (M) \ a \ cdots}

La cohomología de este complejo se denomina cohomología de X de De Rham . El grupo de homología en cero dimensión es isomorfo al espacio vectorial de las funciones localmente constantes de M a R . Así, para un distribuidor compacto, este es el espacio vectorial real cuya dimensión es el número de componentes conectados de M .

Los mapas suaves entre variedades inducen mapas de cadena y las homotopías suaves entre mapas inducen homotopías de cadena.

Categoría de complejos de cadenas

Los complejos de cadenas de módulos K con mapas de cadenas forman una categoría Ch _K , donde K es un anillo conmutativo.

Si V = V y W = W son complejos de cadena, su producto tensorial es un complejo de cadena con elementos de grado n dados por ${\ Displaystyle {} _ {*}}$ ${\ Displaystyle {} _ {*}}$ ${\ Displaystyle V \ otimes W}$

{\ Displaystyle (V \ otimes W) _ {n} = \ bigoplus _ {\ {i, j | i + j = n \}} V_ {i} \ otimes W_ {j}}

y diferencial dado por

{\ Displaystyle \ parcial (a \ otimes b) = \ parcial a \ otimes b + (- 1) ^ {\ left | a \ right |} a \ otimes \ parcial b}

donde un y b son dos vectores homogéneas en V y W , respectivamente, y denota el grado de una . ${\ Displaystyle \ left | a \ right |}$

Este producto tensorial convierte la categoría Ch _K en una categoría monoidal simétrica . El objeto de identidad con respecto a este producto monoidal es el anillo base K visto como un complejo de cadenas en grado 0. El trenzado se da en tensores simples de elementos homogéneos por

{\ Displaystyle a \ otimes b \ mapsto (-1) ^ {\ left | a \ right | \ left | b \ right |} b \ otimes a}

La señal es necesaria para que el trenzado sea un mapa de cadenas.

Además, la categoría de complejos de cadena de módulos K también tiene Hom interno : dados los complejos de cadena V y W , el Hom interno de V y W , denotado Hom ( V , W ), es el complejo de cadena con elementos de grado n dados por y diferencial dado por ${\ Displaystyle \ Pi _ {i} {\ text {Hom}} _ {K} (V_ {i}, W_ {i + n})}$