Conexión afín - Affine connection

Una conexión afín en la esfera rueda el plano tangente afín de un punto a otro. Al hacerlo, el punto de contacto traza una curva en el plano: el desarrollo .

En geometría diferencial , una conexión afín es un objeto geométrico en un múltiple liso que conecta cercanos espacios tangentes , por lo que permite que los campos vectoriales tangentes que se diferencian como si fueran funciones en el colector con valores en un fijo de vector espacial . Las conexiones se encuentran entre los métodos más simples para definir la diferenciación de las secciones de los paquetes de vectores .

La noción de una conexión afín tiene sus raíces en la geometría y el cálculo de tensores del siglo XIX , pero no fue completamente desarrollada hasta principios de la década de 1920, por Élie Cartan (como parte de su teoría general de las conexiones ) y Hermann Weyl (quien usó la noción como una parte de sus fundamentos para la relatividad general ). La terminología se debe a Cartan y tiene su origen en la identificación de espacios tangentes en el espacio euclidiano $R n$ por traducción: la idea es que una elección de conexión afín hace que una multiplicidad se parezca infinitesimalmente al espacio euclidiano no solo suavemente, sino como un espacio afín. .

En cualquier variedad de dimensión positiva hay infinitas conexiones afines. Si la variedad está además dotada de un tensor métrico, entonces existe una elección natural de conexión afín, llamada conexión Levi-Civita . La elección de una conexión afín equivale a prescribir una forma de diferenciar campos vectoriales que satisfaga varias propiedades razonables ( linealidad y regla de Leibniz ). Esto produce una posible definición de una conexión afín como derivada covariante o conexión (lineal) en el haz tangente . La elección de una conexión afín también equivale a la noción de transporte paralelo , que es un método para transportar vectores tangentes a lo largo de curvas. Esto también define un transporte paralelo en el paquete de tramas . El transporte paralelo infinitesimal en el paquete de tramas proporciona otra descripción de una conexión afín, ya sea como una conexión de Cartan para el grupo afín o como una conexión principal en el paquete de tramas.

Los principales invariantes de una conexión afín son su torsión y su curvatura . La torsión mide qué tan cerca se puede recuperar el corchete de Lie de los campos vectoriales de la conexión afín. Las conexiones afines también pueden usarse para definir geodésicas (afines) en una variedad, generalizando las líneas rectas del espacio euclidiano, aunque la geometría de esas líneas rectas puede ser muy diferente de la geometría euclidiana habitual ; las principales diferencias están encapsuladas en la curvatura de la conexión.

Motivación e historia

Una variedad suave es un objeto matemático que se ve localmente como una deformación suave del espacio euclidiano $R n$ : por ejemplo, una curva o superficie suave se ve localmente como una deformación suave de una línea o un plano. Las funciones suaves y los campos vectoriales se pueden definir en las variedades, al igual que en el espacio euclidiano, y las funciones escalares en las variedades se pueden diferenciar de forma natural. Sin embargo, la diferenciación de campos vectoriales es menos sencilla: este es un asunto simple en el espacio euclidiano, porque el espacio tangente de vectores basados en un punto $p$ se puede identificar naturalmente (por traslación) con el espacio tangente en un punto cercano $q$ . En una variedad general, no existe tal identificación natural entre espacios tangentes cercanos, por lo que los vectores tangentes en puntos cercanos no pueden compararse de una manera bien definida. La noción de conexión afín se introdujo para remediar este problema conectando espacios tangentes cercanos. Los orígenes de esta idea se remontan a dos fuentes principales: la teoría de superficies y el cálculo de tensores .

Motivación de la teoría de la superficie

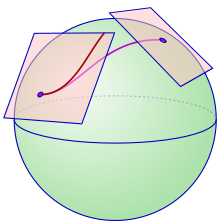
Considere una superficie lisa $S$ en un espacio euclidiano tridimensional. Cerca de cualquier punto, $S$ puede aproximarse por su plano tangente en ese punto, que es un subespacio afín del espacio euclidiano. Los geómetras diferenciales del siglo XIX estaban interesados en la noción de desarrollo en el que una superficie se enrollaba a lo largo de otra, sin resbalar ni torcer . En particular, el plano tangente a un punto de $S$ se puede rodar sobre $S$ : esto debería ser fácil de imaginar cuando $S$ es una superficie como la 2-esfera, que es el límite suave de una región convexa . A medida que el plano tangente se enrolla en $S$ , el punto de trazas de contacto a cabo una curva en $S$ . Por el contrario, dada una curva en $S$ , el plano tangente se puede rodar a lo largo de esa curva. Esto proporciona una forma de identificar los planos tangentes en diferentes puntos a lo largo de la curva: en particular, un vector tangente en el espacio tangente en un punto de la curva se identifica con un vector tangente único en cualquier otro punto de la curva. Estas identificaciones siempre vienen dadas por transformaciones afines de un plano tangente a otro.

Esta noción de transporte paralelo de vectores tangentes, por transformaciones afines, a lo largo de una curva tiene un rasgo característico: el punto de contacto del plano tangente con la superficie siempre se mueve con la curva en traslación paralela (es decir, cuando el plano tangente se rueda a lo largo de la superficie, el punto de contacto se mueve). Esta condición genérica es característica de las conexiones Cartan . En enfoques más modernos, el punto de contacto se ve como el origen en el plano tangente (que entonces es un espacio vectorial), y el movimiento del origen se corrige mediante una traslación, de modo que el transporte paralelo es lineal, en lugar de afín.

Sin embargo, desde el punto de vista de las conexiones de Cartan, los subespacios afines del espacio euclidiano son superficies modelo : son las superficies más simples en el espacio tridimensional euclidiano y son homogéneas bajo el grupo afín del plano, y cada superficie lisa tiene una característica única. superficie del modelo tangente a ella en cada punto. Estas superficies de modelo son geometrías Klein en el sentido de Felix Klein 's programa de Erlangen . De manera más general, un espacio afín $n-$ dimensional es una geometría de Klein para el grupo afín $Aff (n)$ , siendo el estabilizador de un punto el grupo lineal general $GL (n)$ . Una variedad $n$ afín es entonces una variedad que se parece infinitesimalmente a un espacio afín $n-$ dimensional.

Motivación del cálculo tensorial

Históricamente, la gente usaba derivada covariante (o conexión Levi-Civita dada por métrica) para describir la tasa de variación de un vector a lo largo de la dirección de otro vector. Aquí, en el espacio euclidiano bidimensional perforado, el campo vectorial azul

X

envía la forma única

d r

a 0.07 en todas partes. El campo vectorial rojo

Y

envía la forma única

r d θ

a

0.5 r en

todas partes. Apoyado por la métrica

d s 2 = d r 2 + r 2 d θ 2

, la conexión de Levi-Civita

\nabla Y X

es 0 en todas partes, lo que indica

X

no tiene ningún cambio a lo largo de

Y

. En otras palabras,

X

transportes paralelos a lo largo de cada círculo concéntrico .

\nabla X Y = Y / r en

todas partes, lo que envía

r d θ

a 0.5 en todas partes, lo que implica que

Y

tiene una tasa de cambio "constante" en la dirección radial.

La segunda motivación para las conexiones afines proviene de la noción de una derivada covariante de campos vectoriales. Antes del advenimiento de los métodos independientes de coordenadas, era necesario trabajar con campos vectoriales incrustando sus respectivos vectores euclidianos en un atlas . Estos componentes se pueden diferenciar, pero las derivadas no se transforman de forma manejable bajo cambios de coordenadas. Los términos de corrección fueron introducidos por Elwin Bruno Christoffel (siguiendo las ideas de Bernhard Riemann ) en la década de 1870, de modo que la derivada (corregida) de un campo vectorial a lo largo de otro se transformó covariantemente bajo transformaciones de coordenadas; estos términos de corrección posteriormente se conocieron como símbolos de Christoffel .

Esta idea fue desarrollada en la teoría del cálculo diferencial absoluto (ahora conocida como cálculo tensorial ) por Gregorio Ricci-Curbastro y su alumno Tullio Levi-Civita entre 1880 y principios del siglo XX.

El cálculo tensorial realmente cobró vida, sin embargo, con el advenimiento de la teoría de la relatividad general de Albert Einstein en 1915. Unos años después de esto, Levi-Civita formalizó la conexión única asociada a una métrica riemanniana, ahora conocida como Levi-Civita conexión . Las conexiones afines más generales fueron estudiadas alrededor de 1920 por Hermann Weyl , quien desarrolló una base matemática detallada para la relatividad general, y Élie Cartan , quien hizo el vínculo con las ideas geométricas provenientes de la teoría de superficies.

Enfoques

La compleja historia ha llevado al desarrollo de enfoques y generalizaciones muy diversos del concepto de conexión afín.

El enfoque más popular es probablemente la definición motivada por derivadas covariantes. Por un lado, los físicos adoptaron las ideas de Weyl en forma de teoría de gauge y derivadas covariantes de gauge . Por otro lado, la noción de diferenciación covariante fue abstraída por Jean-Louis Koszul , quien definió conexiones (lineales o Koszul) en paquetes vectoriales . En este lenguaje, una conexión afín es simplemente una derivada covariante o conexión (lineal) en el paquete tangente .

Sin embargo, este enfoque no explica la geometría detrás de las conexiones afines ni cómo adquirieron su nombre. El término realmente tiene su origen en la identificación de espacios tangentes en el espacio euclidiano por traducción: esta propiedad significa que el espacio $n$ euclidiano es un espacio afín . (Alternativamente, el espacio euclidiano es un espacio homogéneo principal o torsor bajo el grupo de traducciones, que es un subgrupo del grupo afín.) Como se mencionó en la introducción, hay varias formas de precisar esto: se usa el hecho de que un afín La conexión define una noción de transporte paralelo de campos vectoriales a lo largo de una curva. Esto también define un transporte paralelo en el paquete de tramas . El transporte paralelo infinitesimal en el paquete de tramas proporciona otra descripción de una conexión afín, ya sea como una conexión de Cartan para el grupo afín $Aff (n)$ o como una conexión $GL (n) principal$ en el paquete de tramas.

Definición formal como operador diferencial

Deje que $M$ sea un suave colector y dejar que $Γ (T M)$ sea el espacio de campos vectoriales en $M$ , es decir, el espacio de secciones lisas de la tangente haz $T M$ . Entonces una conexión afín en $M$ es un mapa bilineal

{\ Displaystyle {\ begin {alineado} \ Gamma (\ mathrm {T} M) \ times \ Gamma (\ mathrm {T} M) & \ rightarrow \ Gamma (\ mathrm {T} M) \\ (X, Y ) & \ mapsto \ nabla _ {X} Y \ ,, \ end {alineado}}}

tal que para todo $f$ en el conjunto de funciones suaves en $M$ , escrito $C \infty (M, R)$ , y todos los campos vectoriales $X, Y$ en $M$ :

$\nabla fX Y = f \nabla X Y$ , es decir, $\nabla$ es $C \infty (M, R)$ - lineal en la primera variable;
$\nabla X (fY) = \partial X f Y + f \nabla X Y$ , donde $\partial X$ denota la derivada direccional ; es decir, $\nabla$ satisface la regla de Leibniz en la segunda variable.

Propiedades elementales

De la propiedad 1 anterior se deduce que el valor de $\nabla X Y$ en un punto $x \in M$ depende solo del valor de $X$ en $x$ y no del valor de $X$ en $M - {x}$ . También se deduce de la propiedad 2 anterior que el valor de $\nabla X Y$ en un punto $x \in M$ depende solo del valor de $Y$ en una vecindad de $x$ .
Si $\nabla 1, \nabla 2$ son conexiones afines, entonces el valor en $x$ de $\nabla 1 X Y - \nabla 2 X Y$ puede escribirse $Γ x (X x, Y x)$ donde ${\ Displaystyle \ Gamma _ {x}: \ mathrm {T} _ {x} M \ times \ mathrm {T} _ {x} M \ to \ mathrm {T} _ {x} M}$ es bilineal y depende suavemente de $x$ (es decir, define un homomorfismo de haz suave ). Por el contrario, si $\nabla$ es una conexión afín y $Γ$ es un homomorfismo de haz bilineal tan suave (llamado forma de conexión en $M$ ), entonces $\nabla + Γ$ es una conexión afín.
Si $M$ es un subconjunto abierto de $R n$ , entonces el paquete tangente de $M$ es el paquete trivial $M \times R n$ . En esta situación hay una conexión afín canónica $d$ en $M$ : cualquier campo vectorial $Y$ viene dado por una función uniforme $V$ de $M$ a $R n$ ; entonces $d X Y$ es el campo vectorial correspondiente a la función suave $d V (X) = \partial X Y$ de $M$ a $R n$ . Cualquier otra conexión afín $\nabla$ en $M$ , por lo tanto se puede escribir $\nabla = d + Γ$ , donde $Γ$ es una forma de conexión en $M$ .
De manera más general, una trivialización local del haz tangente es un isomorfismo del haz entre la restricción de $T M$ a un subconjunto abierto $U$ de $M$ , y $U \times R n$ . La restricción de una conexión afín $\nabla$ a $U$ puede entonces escribirse en la forma $d + Γ$ donde $Γ$ es una forma de conexión en $U$ .

Transporte paralelo para conexiones afines

Transporte paralelo de un vector tangente a lo largo de una curva en la esfera.

La comparación de vectores tangentes en diferentes puntos de una variedad generalmente no es un proceso bien definido. Una conexión afín proporciona una forma de remediar esto utilizando la noción de transporte paralelo y, de hecho, esto puede usarse para dar una definición de una conexión afín.

Sea $M$ una variedad con una conexión afín $\nabla$ . Entonces, se dice que un campo vectorial $X$ es paralelo si $\nabla X = 0$ en el sentido de que para cualquier campo vectorial $Y$ , $\nabla Y X = 0$ . Hablando intuitivamente, los vectores paralelos tienen todas sus derivadas iguales a cero y, por lo tanto, en cierto sentido son constantes . Mediante la evaluación de un campo de vector paralelo en dos puntos $x$ y $Y$ , una identificación entre un vector tangente en $x$ y uno en $y$ se obtiene. Se dice que tales vectores tangentes son transportes paralelos entre sí.

Los campos vectoriales paralelos distintos de cero no existen, en general, porque la ecuación $\nabla X = 0$ es una ecuación diferencial parcial que está sobredeterminada : la condición de integrabilidad para esta ecuación es la desaparición de la curvatura de $\nabla$ (ver más abajo). Sin embargo, si esta ecuación está restringida a una curva de $x$ a $y$ se convierte en una ecuación diferencial ordinaria . Entonces hay una solución única para cualquier valor inicial de $X$ en $x$ .

Más precisamente, si $γ : I \to M$ una curva suave parametrizada por un intervalo $[a, b]$ y $ξ \in T x M$ , donde $x = γ (a)$ , entonces un campo vectorial $X a lo$ largo de $γ$ (y en particular, el valor de este campo vectorial en $y = γ (b)$ ) se denomina transporte paralelo de $ξ a lo$ largo de $γ$ si

$\nabla γ ' (t) X = 0$ , para todo $t \in [a, b]$
$X γ (a) = ξ$ .

Formalmente, los primeros condición significa que $X$ es paralelo con respecto a la conexión de presión de regreso en el haz de retroceso $γ * T M$ . Sin embargo, en una trivialización local es un sistema de primer orden de ecuaciones diferenciales ordinarias lineales , que tiene una solución única para cualquier condición inicial dada por la segunda condición (por ejemplo, por el teorema de Picard-Lindelöf ).

Así, el transporte paralelo proporciona una forma de mover vectores tangentes a lo largo de una curva utilizando la conexión afín para mantenerlos "apuntando en la misma dirección" en un sentido intuitivo, y esto proporciona un isomorfismo lineal entre los espacios tangentes en los dos extremos de la curva. El isomorfismo obtenido de esta manera dependerá en general de la elección de la curva: si no es así, entonces el transporte paralelo a lo largo de cada curva se puede usar para definir campos vectoriales paralelos en $M$ , lo que solo puede ocurrir si la curvatura de $\nabla$ es cero. .

Un isomorfismo lineal está determinado por su acción sobre una base o marco ordenado . Por tanto, el transporte paralelo también se puede caracterizar como una forma de transportar elementos del haz de tramas (tangente) $GL (M) a lo$ largo de una curva. En otras palabras, la conexión afín proporciona una elevación de cualquier curva $γ$ en $M$ a una curva $γ̃$ en $GL (M)$ .

Definición formal en el paquete de marcos

Una conexión afín también puede ser definido como un director $GL (n)$ conexión $ω$ en el marco de haz $F M$ o $GL (M)$ de un colector $M$ . Más detalladamente, $ω$ es un mapa suave desde el paquete tangente $T (F M)$ del paquete de marcos al espacio de $n \times n$ matrices (que es el álgebra de Lie $gl (n)$ del grupo de Lie $GL (n)$ de invertible $n \times n$ matrices) que satisfacen dos propiedades:

$ω$ es equivariante con respecto a la acción de $GL (n)$ sobre $T (F M)$ y $gl (n)$ ;
$ω (X ξ) = ξ$ para cualquier $ξ$ en $gl (n)$ , donde $X ξ$ es el campo vectorial en $F M$ correspondiente a $ξ$ .

Tal conexión $ω$ define inmediatamente una derivada covariante no solo en el paquete tangente, sino en los paquetes de vectores asociados a cualquier representación de grupo de $GL (n)$ , incluidos los paquetes de tensores y densidades de tensor . Por el contrario, una conexión afín en el haz tangente determina una conexión afín en el haz de tramas, por ejemplo, al requerir que $ω$ desaparezca en los vectores tangentes a las elevaciones de las curvas al haz de tramas definido por el transporte paralelo.

El paquete de marcos también viene equipado con una forma de soldadura $θ : T (F M) \to R n$ que es horizontal en el sentido de que desaparece en vectores verticales como los valores de puntos de los campos vectoriales $X ξ$ : de hecho, $θ$ se define primero por proyectar un vector tangente (a $F M$ en un marco $f$ ) a $M$ , luego tomando las componentes de este vector tangente en $M$ con respecto al marco $f$ . Tenga en cuenta que $θ$ también es $GL (n)$ -equivariante (donde $GL (n)$ actúa sobre $R n$ mediante la multiplicación de matrices).

El par $(θ, ω)$ define un isomorfismo de paquete de $T (F M)$ con el paquete trivial $F M \times aff (n)$ , donde $aff (n)$ es el producto cartesiano de $R n$ y $gl (n)$ (visto como el Álgebra de mentiras del grupo afín, que en realidad es un producto semidirecto (ver más abajo).

Conexiones afines como conexiones Cartan

Las conexiones afines se pueden definir dentro del marco general de Cartan. En el enfoque moderno, esto está estrechamente relacionado con la definición de conexiones afines en el paquete de tramas. De hecho, en una formulación, una conexión de Cartan es un paralelismo absoluto de un paquete principal que satisface propiedades adecuadas. Desde este punto de vista la $aff (n)$ -valued de una sola forma $(θ, ω): T (F M) \to aff (n)$ sobre el haz de marco (de un colector de affine ) es una conexión de Cartan. Sin embargo, el enfoque original de Cartan era diferente de este en varias formas:

el concepto de paquetes de marcos o paquetes principales no existía;
se veía una conexión en términos de transporte paralelo entre puntos infinitesimalmente cercanos;
este transporte paralelo era más afín que lineal;
los objetos transportados no eran vectores tangentes en el sentido moderno, sino elementos de un espacio afín con un punto marcado, que la conexión de Cartan identifica en última instancia con el espacio tangente.

Explicaciones e intuición histórica

Los puntos que acabamos de plantear son más fáciles de explicar al revés, partiendo de la motivación proporcionada por la teoría de la superficie. En esta situación, aunque los planos que se desplazan sobre la superficie son planos tangentes en un sentido ingenuo, la noción de espacio tangente es realmente una noción infinitesimal , mientras que los planos, como subespacios afines de $R 3$ , tienen una extensión infinita . Sin embargo, todos estos planos afines tienen un punto marcado, el punto de contacto con la superficie, y son tangentes a la superficie en este punto. Por tanto, la confusión surge porque un espacio afín con un punto marcado puede identificarse con su espacio tangente en ese punto. Sin embargo, el transporte paralelo definido por rolling no fija este origen: es más afín que lineal; el transporte lineal paralelo se puede recuperar aplicando una traslación.

Haciendo abstracción esta idea, un colector de afín debe por lo tanto ser un $n$ -manifold $M$ con un afín espacio $A x$ , de dimensión $n$ , adjunto a cada $x \in M$ en un punto marcado $un x \in A x$ , junto con un método para el transporte de elementos de estos espacios afines a lo largo de cualquier curva $C$ en $M$ . Este método es necesario para satisfacer varias propiedades:

para dos puntos cualesquiera $x, y$ en $C$ , el transporte paralelo es una transformación afín de $A x$ a $A y$ ;
el transporte paralelo se define infinitesimalmente en el sentido de que es diferenciable en cualquier punto de $C$ y depende sólo del vector tangente a $C$ en ese punto;
la derivada del transporte paralelo en $x$ determina un isomorfismo lineal de $T x M$ a $T a x A x$ .

Estos dos últimos puntos son bastante difíciles de precisar, por lo que las conexiones afines se definen más a menudo infinitesimalmente. Para motivar esto, basta con considerar cómo los marcos de referencia afines se transforman infinitesimalmente con respecto al transporte paralelo. (Este es el origen del método de Cartan de mover cuadros .) Un cuadro afín en un punto consiste en una lista $(p, e 1,\dots e n)$ , donde $p \in A x$ y $e i$ forman una base de $T p (A x)$ . La conexión afín viene dada simbólicamente por un sistema diferencial de primer orden.

{\ Displaystyle (*) {\ begin {cases} \ mathrm {d} {p} & = \ theta ^ {1} \ mathbf {e} _ {1} + \ cdots + \ theta ^ {n} \ mathbf { e} _ {n} \\\ mathrm {d} \ mathbf {e} _ {i} & = \ omega _ {i} ^ {1} \ mathbf {e} _ {1} + \ cdots + \ omega _ {i} ^ {n} \ mathbf {e} _ {n} \ end {cases}} \ quad i = 1,2, \ ldots, n}

definido por una colección de formas $únicas$ $(θ j, ω j yo)$ . Geométricamente, un marco afín sufre un desplazamiento que viaja a lo largo de una curva $γ$ desde $γ (t)$ a $γ (t + δt)$ dado (aproximadamente, o infinitesimalmente) por

{\ Displaystyle {\ begin {alineado} p (\ gamma (t + \ delta t)) - p (\ gamma (t)) & = \ left (\ theta ^ {1} \ left (\ gamma '(t) \ derecha) \ mathbf {e} _ {1} + \ cdots + \ theta ^ {n} \ left (\ gamma '(t) \ right) \ mathbf {e} _ {n} \ right) \ mathrm {\ delta } t \\\ mathbf {e} _ {i} (\ gamma (t + \ delta t)) - \ mathbf {e} _ {i} (\ gamma (t)) & = \ left (\ omega _ {i } ^ {1} \ left (\ gamma '(t) \ right) \ mathbf {e} _ {1} + \ cdots + \ omega _ {i} ^ {n} \ left (\ gamma' (t) \ derecha) \ mathbf {e} _ {n} \ derecha) \ delta t \,. \ end {alineado}}}

Además, se requiere que los espacios afines $A x$ sean tangentes a $M$ en el sentido informal de que el desplazamiento de $a x a lo$ largo de $γ$ se puede identificar (aproximadamente o infinitesimalmente) con el vector tangente $γ' (t)$ a $γ$ en $x = γ (t)$ (que es el desplazamiento infinitesimal de $x$ ). Ya que

{\ Displaystyle a_ {x} (\ gamma (t + \ delta t)) - a_ {x} (\ gamma (t)) = \ theta \ left (\ gamma '(t) \ right) \ delta t \ ,, }

donde $θ$ se define por $θ (X) = θ 1 (X) e 1 +\dots + θ n (X) e n$ , esta identificación viene dada por $θ$ , por lo que el requisito es que $θ$ debe ser un isomorfismo lineal en cada punto.

El espacio afín tangencial $A x$ se identifica así intuitivamente con una vecindad afín infinitesimal de $x$ .

El punto de vista moderno hace que toda esta intuición sea más precisa utilizando paquetes principales (la idea esencial es reemplazar un marco o un marco variable por el espacio de todos los marcos y funciones en este espacio). También se basa en la inspiración de Felix Klein 's programa de Erlangen , en el que una geometría se define para ser un espacio homogéneo . El espacio afín es una geometría en este sentido y está equipado con una conexión Cartan plana . Así, una variedad afín general se ve como una deformación curva de la geometría del modelo plano del espacio afín.

Espacio afín como la geometría del modelo plano

Definición de un espacio afín

De manera informal, un espacio afín es un espacio vectorial sin una elección fija de origen . Describe la geometría de puntos y vectores libres en el espacio. Como consecuencia de la falta de origen, los puntos en el espacio afín no se pueden sumar, ya que esto requiere una elección de origen con el que formar la ley del paralelogramo para la adición de vectores. Sin embargo, se puede agregar un vector $v$ a un punto $p$ colocando el punto inicial del vector en $p$ y luego transportando $p$ al punto terminal. La operación así descrita $p \to p + v$ es la traslación de $p a lo$ largo de $v$ . En términos técnicos, el espacio $n$ afín es un conjunto $A n$ equipado con una acción transitiva libre del grupo de vectores $R n$ sobre él a través de esta operación de traslación de puntos: $A n$ es, por tanto, un espacio homogéneo principal para el grupo de vectores $R n$ .

El grupo lineal general $GL (n)$ es el grupo de transformaciones de $R n$ que preservan la estructura lineal de $R n$ en el sentido de que $T (av + bw) = aT (v) + bT (w)$ . Por analogía, el grupo afín $Aff (n)$ es el grupo de transformaciones de $A n que$ conserva la estructura afín . Por tanto, $φ \in Aff (n)$ debe conservar las traducciones en el sentido de que

{\ Displaystyle \ varphi (p + v) = \ varphi (p) + T (v)}

donde $T$ es una transformación lineal general. El mapa que envía $φ \in Aff (n)$ a $T \in GL (n)$ es un homomorfismo de grupo . Su núcleo es el grupo de traducciones $R n$ . El estabilizador de cualquier punto $p$ en $A$ se puede identificar con $GL (n)$ usando esta proyección: esto realiza el grupo afín como un producto semidirecto de $GL (n)$ y $R n$ , y el espacio afín como el espacio homogéneo $Aff (n) / GL (n)$ .

Marcos afines y la conexión afín plana

Un marco afín para $A$ consta de un punto $p \in A$ y una base $(e 1,\dots e n)$ del espacio vectorial $T p A = R n$ . El grupo lineal general $GL (n)$ actúa libremente sobre el conjunto $F A$ de todos los fotogramas afines fijando $py$ transformando la base $(e 1,\dots e n)$ de la forma habitual, y el mapa $π$ enviando un fotograma afín $(p; e 1, ... e n)$ a $p$ es la aplicación cociente . Por lo tanto $F A$ es un director $GL (n)$ -bundle sobre $A$ . La acción de $GL (n) se$ extiende naturalmente a una acción transitiva libre del grupo afín $Aff (n)$ sobre $F A$ , de modo que $F A$ es un $Aff (n)$ - torsor , y la elección de un marco de referencia identifica $F A \to A$ con el paquete principal $Aff (n) \to Aff (n) / GL (n)$ .

En $F A$ hay una colección de $n + 1$ funciones definidas por

{\ Displaystyle \ pi (p; \ mathbf {e} _ {1}, \ dots, \ mathbf {e} _ {n}) = p}

(como antes) y

{\ Displaystyle \ varepsilon _ {i} (p; \ mathbf {e} _ {1}, \ dots, \ mathbf {e} _ {n}) = \ mathbf {e} _ {i} \ ,.}

Después de elegir un punto base para $A$ , todas estas son funciones con valores en $R n$ , por lo que es posible tomar sus derivadas exteriores para obtener formas 1 diferenciales con valores en $R n$ . Dado que las funciones $ε i$ dan una base para $R n$ en cada punto de $F A$ , estas formas 1 deben poder expresarse como sumas de la forma

{\ Displaystyle {\ begin {alineado} \ mathrm {d} \ pi & = \ theta ^ {1} \ varepsilon _ {1} + \ cdots + \ theta ^ {n} \ varepsilon _ {n} \\\ mathrm {d} \ varepsilon _ {i} & = \ omega _ {i} ^ {1} \ varepsilon _ {1} + \ cdots + \ omega _ {i} ^ {n} \ varepsilon _ {n} \ end { alineado}}}

para alguna colección $(θ i, ω k j) 1 \leq i, j, k \leq n$ de formas $uniformes de$ valor real en $Aff ($ $n$ $)$ . Este sistema de uno en formularios en el fibrado principal $F A \to A$ define la conexión afín en $A$ .

Tomando la derivada exterior por segunda vez, y usando el hecho de que $d 2 = 0$ así como la independencia lineal de $ε i$ , se obtienen las siguientes relaciones:

{\ Displaystyle {\ begin {alineado} \ mathrm {d} \ theta ^ {j} - \ sum _ {i} \ omega _ {i} ^ {j} \ wedge \ theta ^ {i} & = 0 \\ \ mathrm {d} \ omega _ {i} ^ {j} - \ sum _ {k} \ omega _ {k} ^ {j} \ wedge \ omega _ {i} ^ {k} & = 0 \ ,. \ end {alineado}}}

Estas son las ecuaciones de Maurer-Cartan para el grupo de Lie $Aff (n)$ (identificado con $F A$ por la elección de un marco de referencia). Es más:

el sistema de Pfaff $θ j = 0$ (para todos $j$ ) es integrable , y sus variedades integrales son las fibras del haz principal de $Aff (n) \to A$ .
el sistema de Pfaffian $ω j yo = 0$ (para todas $i, j$ ) es también integrable, y sus variedades integrales definir transporte paralelo en $F A$ .

Así las formas $(ω j yo)$ Definir un plano conexión principal en $F A \to A$ .

Para una comparación estricta con la motivación, se debe en realidad definir transporte paralelo en un principal $Aff (n)$ -bundle sobre $A$ . Esto se puede hacer tirando de $F A$ hacia atrás mediante el mapa suave $φ : R n \times A \to A$ definido por traslación. Entonces el compuesto $φ' * F A \to F A \to A$ es un paquete principal de $Aff (n)$ sobre $A$ , y las formas $(θ i, ω k j)$ tire hacia atrás para dar una conexión principal plana $Aff (n)$ en este paquete.

Geometrías afines generales: definiciones formales

Un espacio afín, como prácticamente cualquier geometría de Klein suave , es un colector equipado con una conexión Cartan plana. Las variedades afines o geometrías afines más generales se obtienen fácilmente eliminando la condición de planitud expresada por las ecuaciones de Maurer-Cartan. Hay varias formas de abordar la definición y se darán dos. Ambas definiciones se ven facilitadas por la comprensión de que las formas 1 $(θ i, ω k j)$ en el modelo plano se ajustan para dar una forma 1 con valores en el álgebra de Lie $aff (n)$ del grupo afín $Aff (n)$ .

En estas definiciones, $M$ es una variedad $n$ suave y $A = Aff (n) / GL (n)$ es un espacio afín de la misma dimensión.

Definición vía paralelismo absoluto

Deje que $M$ sea un colector, y $P$ un principal $GL (n)$ -bundle sobre $M$ . Entonces, una conexión afín es una forma 1 $η$ en $P$ con valores en $aff (n) que$ satisfacen las siguientes propiedades

$η$ es equivariante con respecto a la acción de $GL (n)$ sobre $P$ y $aff (n)$ ;
$η (X ξ) = ξ$ para todo $ξ$ en el álgebra de Lie $gl (n)$ de todas las $n \times n$ matrices;
$η$ es un isomorfismo lineal de cada espacio tangente de $P$ con $aff (n)$ .

La última condición significa que $η$ es un paralelismo absoluto en $P$ , es decir, identifica el paquete tangente de $P$ con un paquete trivial (en este caso $P \times aff (n)$ ). El par $(P, η)$ define la estructura de una geometría afín en $M$ , convirtiéndola en una variedad afín .

El álgebra de Lie afín $aff (n) se$ divide como un producto semidirecto de $R n$ y $gl (n),$ por lo que $η$ puede escribirse como un par $(θ, ω)$ donde $θ$ toma valores en $R n$ y $ω$ toma valores en $gl (n)$ . Las condiciones 1 y 2 son equivalentes a que $ω$ sea una conexión $GL (n) principal$ y $θ$ sea una forma 1 equivariante horizontal, que induce un homomorfismo de haz de $T M$ al haz asociado $P \times GL (n) R n$ . La condición 3 es equivalente al hecho de que este homomorfismo de haz es un isomorfismo. (Sin embargo, esta descomposición es una consecuencia de la estructura bastante especial del grupo afín.) Dado que $P$ es el paquete de tramas de $P \times GL (n) R n$ , se deduce que $θ$ proporciona un isomorfismo de paquete entre $P$ y el paquete de tramas $F M$ de $M$ ; este recupera la definición de una conexión afín como principal $GL (n)$ -conexión en $F M$ .

Las formas 1 que surgen en el modelo plano son solo los componentes de $θ$ y $ω$ .

Definición como conexión afín principal

Una conexión afín en $M$ es un $Aff (n)$ -bundle $Q principal$ sobre $M$ , junto con un principal $GL (n)$ -subbundle $P$ de $Q$ y una principal $Aff (n)$ -connection $α$ (una forma 1 en $Q$ con valores en $aff (n)$ ) que satisface la siguiente condición de Cartan (genérica) . El componente $R n$ del retroceso de $α$ a $P$ es una forma 1 equivariante horizontal y, por lo tanto, define un homomorfismo de haz de $T M$ a $P \times GL (n) R n$ : se requiere que sea un isomorfismo.

Relación con la motivación

Dado que $Aff (n)$ actúa sobre $A$ , hay, asociado al haz principal $Q$ , un haz $A = Q \times Aff (n) A$ , que es un haz de fibras sobre $M$ cuya fibra en $x$ en $M$ es un espacio afín $A x$ . Una sección $a$ de $A$ (que define un punto marcado $a x$ en $A x$ para cada $x \in M$ ) determina un subconjunto principal $GL (n)$ $P$ de $Q$ (como el conjunto de estabilizadores de estos puntos marcados) y viceversa. La conexión principal $α$ define una conexión de Ehresmann en este paquete, de ahí una noción de transporte paralelo. La condición de Cartan asegura que la sección distinguida $a$ siempre se mueva en transporte paralelo.

Otras propiedades

Curvatura y torsión

La curvatura y la torsión son los principales invariantes de una conexión afín. Como existen muchas formas equivalentes de definir la noción de conexión afín, existen muchas formas diferentes de definir la curvatura y la torsión.

Desde el punto de vista de la conexión de Cartan, la curvatura es la falla de la conexión afín $η$ para satisfacer la ecuación de Maurer-Cartan

{\ Displaystyle \ mathrm {d} \ eta + {\ tfrac {1} {2}} [\ eta \ wedge \ eta] = 0,}

donde el segundo término en el lado izquierdo es el producto de la cuña usando el corchete de Lie en $aff (n)$ para contraer los valores. Al expandir $η$ en el par $(θ, ω)$ y usar la estructura del álgebra de Lie $aff (n)$ , este lado izquierdo se puede expandir en las dos fórmulas

{\ Displaystyle \ mathrm {d} \ theta + \ omega \ wedge \ theta \ quad {\ text {y}} \ quad \ mathrm {d} \ omega + \ omega \ wedge \ omega \ ,,}

donde los productos de la cuña se evalúan mediante la multiplicación de matrices. La primera expresión se llama torsión de la conexión y la segunda también se llama curvatura.

Estas expresiones son 2 formas diferenciales en el espacio total de un paquete de tramas. Sin embargo, son horizontales y equivariantes y, por lo tanto, definen objetos tensoriales. Estos se pueden definir directamente a partir de la derivada covariante inducida $\nabla$ en $T M$ como sigue.

La torsión viene dada por la fórmula

{\ displaystyle T ^ {\ nabla} (X, Y) = \ nabla _ {X} Y- \ nabla _ {Y} X- [X, Y].}

Si la torsión desaparece, se dice que la conexión está libre de torsión o simétrica .

La curvatura viene dada por la fórmula

{\ Displaystyle R_ {X, Y} ^ {\ nabla} Z = \ nabla _ {X} \ nabla _ {Y} Z- \ nabla _ {Y} \ nabla _ {X} Z- \ nabla _ {[X , Y]} Z.}

Tenga en cuenta que $[X, Y]$ es el corchete de Lie de los campos vectoriales

{\ Displaystyle [X, Y] = \ izquierda (X ^ {j} \ parcial _ {j} Y ^ {i} -Y ^ {j} \ parcial _ {j} X ^ {i} \ derecha) \ parcial _{I}}

en notación de Einstein . Esto es independiente de la elección del sistema de coordenadas y

{\ estilo de visualización \ parcial _ {i} = \ izquierda ({\ frac {\ parcial} {\ parcial \ xi ^ {i}}} \ derecha) _ {p} \ ,,}

el vector tangente en el punto $p$ de la $i-$ ésima curva de coordenadas . Las $\partial i$ son una base natural para el espacio tangente en el punto $p$ , y las $X i$ las coordenadas correspondientes para el campo vectorial $X = X i \partial i$ .

Cuando tanto la curvatura como la torsión desaparecen, la conexión define una estructura de álgebra anterior a la de Lie en el espacio de las secciones globales del haz tangente.

La conexión Levi-Civita

Si $(M, g)$ es una variedad de Riemann, entonces hay una conexión afín única $\nabla$ en $M$ con las dos propiedades siguientes:

la conexión está libre de torsión, es decir, $T \nabla$ es cero, de modo que $\nabla X Y - \nabla Y X = [X, Y]$ ;
El transporte paralelo es una isometría, es decir, se conservan los productos internos (definidos mediante $g$ ) entre los vectores tangentes.

Esta conexión se llama conexión Levi-Civita .

El término "simétrico" se utiliza a menudo en lugar de libre de torsión para la primera propiedad. La segunda condición significa que la conexión es una conexión métrica en el sentido de que la métrica de Riemann $g$ es paralela: $\nabla g = 0$ . Para una conexión libre de torsión, la condición es equivalente a la identidad $X g (Y, Z)$ = $g (\nabla X Y, Z)$ + $g (Y, \nabla X Z)$ , "compatibilidad con la métrica". En coordenadas locales, los componentes de la forma se denominan símbolos de Christoffel : debido a la singularidad de la conexión Levi-Civita, existe una fórmula para estos componentes en términos de los componentes de $g$ .

Geodésicas

Dado que las líneas rectas son un concepto en geometría afín, las conexiones afines definen una noción generalizada de líneas rectas (parametrizadas) en cualquier variedad afín, llamadas geodésicas afines. En resumen, una curva paramétrica $γ : I \to M$ es una línea recta si su vector tangente permanece paralelo y equipollente consigo mismo cuando se transporta a lo largo de $γ$ . Desde el punto de vista lineal, una conexión afín $M$ distingue las geodésicas afines de la siguiente manera: una curva suave $γ : I \to M$ es una geodésica afín si $γ̇$ se transporta en paralelo a lo largo de $γ$ , es decir

{\ Displaystyle \ tau _ {t} ^ {s} {\ dot {\ gamma}} (s) = {\ dot {\ gamma}} (t)}

donde $τ s t : T γ s M \to T γ t M$ es el mapa de transporte paralelo que define la conexión.

En términos de la conexión infinitesimal $\nabla$ , la derivada de esta ecuación implica

{\ Displaystyle \ nabla _ {{\ dot {\ gamma}} (t)} {\ dot {\ gamma}} (t) = 0}

para toda $t \in I$ .

Por el contrario, cualquier solución de esta ecuación diferencial produce una curva cuyo vector tangente se transporta en paralelo a lo largo de la curva. Para cada $x \in M$ y cada $X \in T x M$ , existe una $γ$ geodésica afín única $:$ $I$ $\to$ $M$ con $γ (0) = x$ y $γ̇ (0) = X$ y donde $I$ es el intervalo abierto máximo en $R$ , que contiene 0, en el que se define la geodésica. Esto se deriva del teorema de Picard-Lindelöf y permite la definición de un mapa exponencial asociado a la conexión afín.

En particular, cuando $M$ es una variedad ( pseudo -) riemanniana y $\nabla$ es la conexión Levi-Civita , entonces las geodésicas afines son las geodésicas habituales de la geometría riemanniana y son las curvas que minimizan la distancia localmente.

Las geodésicas definidas aquí a veces se llaman affinely parametrizan , ya que una línea recta dada en $M$ determina una curva paramétrica $γ$ través de la línea hasta una selección de affine reparametrización $γ (t) \to γ (a + b)$ , en donde $un$ y $b$ son constantes . El vector tangente a una geodésica afín es paralelo y equipollente a lo largo de sí mismo. Una geodésica no parametrizada, o una que es simplemente paralela a sí misma sin ser necesariamente equipollente, solo necesita satisfacer

{\ Displaystyle \ nabla _ {\ dot {\ gamma}} {\ dot {\ gamma}} = k {\ dot {\ gamma}}}

para alguna función $k$ definida a lo largo de $γ$ . Las geodésicas no parametrizadas a menudo se estudian desde el punto de vista de las conexiones proyectivas .

Desarrollo

Una conexión afín define una noción de desarrollo de curvas. Intuitivamente, el desarrollo captura la noción de que si $x t$ es una curva en $M$ , entonces el espacio tangente afín en $x 0$ se puede rodar a lo largo de la curva. Al hacerlo, el punto de contacto marcado entre el espacio tangente y la variedad traza una curva $C t$ en este espacio afín: el desarrollo de $x t$ .

En términos formales, sea $τ 0 t : T x t M \to T x 0 M$ sea el mapa de transporte paralelo lineal asociado a la conexión afín. Entonces el desarrollo $C t$ es la curva en $T x 0 M$ comienza en 0 y es paralela a la tangente de $x t$ para todo el tiempo $t$ :

{\ Displaystyle {\ dot {C}} _ ​​{t} = \ tau _ {t} ^ {0} {\ dot {x}} _ {t} \ ,, \ quad C_ {0} = 0.}

En particular, $x t$ es un geodésica si y sólo si su desarrollo es una línea recta affinely parametrizada en $T x 0 M$ .

Revisión de la teoría de superficies

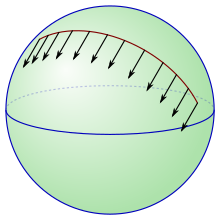
Si $M$ es una superficie en $R 3$ , es fácil ver que $M$ tiene una conexión afín natural. Desde el punto de conexión lineal de vista, la derivada covariante de un campo vectorial se define mediante la diferenciación del campo vectorial, visto como un mapa de $M$ a $R 3$ , y después se proyecta el resultado ortogonalmente de nuevo en los espacios tangentes de $M$ . Es fácil ver que esta conexión afín está libre de torsión. Además, es una conexión métrica con respecto a la métrica de Riemann en $M$ inducida por el producto interno en $R 3$ , por lo que es la conexión Levi-Civita de esta métrica.

Ejemplo: la esfera unitaria en el espacio euclidiano

Sea $⟨,⟩$ el producto escalar habitual en $R 3$ , y sea $S 2$ la esfera unitaria. El espacio tangente a $S 2$ en un punto $x$ se identifica naturalmente con el subespacio vectorial de $R 3 que$ consta de todos los vectores ortogonales $ax$ . De ello se deduce que un campo vectorial $Y$ en $S 2$ puede verse como un mapa $Y : S 2 \to R 3$ que satisface

{\ Displaystyle \ langle Y_ {x}, x \ rangle = 0 \ ,, \ quad \ forall x \ in \ mathbf {S} ^ {2}.}

Denote como $d Y$ el diferencial (matriz jacobiana) de tal mapa. Entonces tenemos:

Lema . La formula

{\ Displaystyle (\ nabla _ {Z} Y) _ {x} = \ mathrm {d} Y_ {x} (Z_ {x}) + \ langle Z_ {x}, Y_ {x} \ rangle x}

define una conexión afín en

S 2

con torsión que desaparece.

Prueba . Es sencillo demostrar que

\nabla

satisface la identidad de Leibniz y es

C \infty (S 2)

lineal en la primera variable. Entonces, todo lo que debe probarse aquí es que el mapa anterior de hecho define un campo vectorial tangente. Es decir, necesitamos demostrar que para todo

x

en

S 2

{\ displaystyle {\ bigl \ langle} (\ nabla _ {Z} Y) _ {x}, x {\ bigr \ rangle} = 0 \,. \ qquad {\ text {(Eq.1)}}}

Considere el mapa

{\ Displaystyle {\ begin {alineado} f: \ mathbf {S} ^ {2} & \ to \ mathbf {R} \\ x & \ mapsto \ langle Y_ {x}, x \ rangle \,. \ end {alineado }}}

El mapa f es constante, por lo que su diferencial desaparece. En particular

{\ Displaystyle \ mathrm {d} f_ {x} (Z_ {x}) = {\ bigl \ langle} (\ mathrm {d} Y) _ {x} (Z_ {x}), x (\ gamma '( t)) {\ bigr \ rangle} + \ langle Y_ {x}, Z_ {x} \ rangle = 0 \ ,.}

Sigue la ecuación 1 anterior. QED

Ver también

Notas

Citas

Referencias

Akivis, MA; Rosenfeld, Boris (1993). Élie Cartan (1869-1951) . Traducido por Goldberg, VV AMS . ISBN 978-0-8218-5355-9.
Lee, John M. (1997). Colectores de Riemann: una introducción a la curvatura . Textos de Posgrado en Matemáticas . 176 . Nueva York: Springer-Verlag . ISBN 978-0-387-98322-6. OCLC 54850593 .
Lee, John M. (2018). Introducción a los colectores de Riemann (2ª ed.). Springer Verlag . ISBN 978-3-319-91755-9.

Bibliografía

Referencias históricas primarias

Christoffel, Elwin Bruno (1869), "Über die Transformation der homogenen Differentialausdrücke zweiten Grades" , Journal für die reine und angewandte Mathematik , 1869 (70): 46–70, doi : 10.1515 / crll.1869.70.46
Levi-Civita, Tullio (1917), "Nozione di paralelismo in una varietà qualunque e conseguente specificazione geometrica della curvatura Riemanniana" , Rend. Circ. Estera. Palermo , 42 : 173–205, doi : 10.1007 / bf03014898
Cartan, Élie (1923), "Sur les variétés à connexion affine, et la théorie de la relativité généralisée (première partie)", Annales Scientifiques de l'École Normale Supérieure , 40 : 325–412, doi : 10.24033 / asens.751
Cartan, Élie (1924), "Sur les variétés à connexion affine, et la théorie de la relativité généralisée (première partie) (Suite)", Annales Scientifiques de l'École Normale Supérieure , 41 : 1–25, doi : 10.24033 / asens.753
Cartan, Élie (1986), Sobre las variedades con conexión afín y la teoría de la relatividad general , Humanities Press

El tratamiento de Cartan de las conexiones afines motivado por el estudio de la teoría de la relatividad. Incluye una discusión detallada de la física de los marcos de referencia y cómo la conexión refleja la noción física de transporte a lo largo de una línea de mundo .

Cartan, Élie (1926), "Espaces à connexion affine, projective et conforme", Acta Math. , 48 : 1–42, doi : 10.1007 / BF02629755

Una explicación más matemáticamente motivada de las conexiones afines.

Cartan, Élie (1951), con apéndices de Robert Hermann (ed.), Geometry of Riemannian Spaces (traducción de James Glazebrook de Leçons sur la géométrie des espaces de Riemann , 2a ed.), Math Sci Press, Massachusetts (publicado en 1983) , ISBN 978-0-915692-34-7.

Conexiones afines desde el punto de vista de la geometría riemanniana . Los apéndices de Robert Hermann discuten la motivación de la teoría de la superficie, así como la noción de conexiones afines en el sentido moderno de Koszul. Desarrolla las propiedades básicas del operador diferencial ∇ y las relaciona con las conexiones afines clásicas en el sentido de Cartan.

Weyl, Hermann (1918), Raum, Zeit, Materie (5 ediciones hasta 1922, con notas de Jürgen Ehlers (1980), traducido 4a edición Space, Time, Matter de Henry Brose, 1922 (Methuen, reimpreso en 1952 por Dover) ed. ), Springer, Berlín, ISBN 0-486-60267-2

Referencias secundarias

Kobayashi, Shoshichi; Nomizu, Katsumi (1996), Fundamentos de la geometría diferencial, Vols. 1 y 2 (Nueva ed.), Wiley-Interscience, ISBN 0-471-15733-3.

Esta es la referencia principal para los detalles técnicos del artículo. El volumen 1, capítulo III, ofrece una descripción detallada de las conexiones afines desde la perspectiva de los principales paquetes en una variedad, transporte paralelo, desarrollo, geodésicas y operadores diferenciales asociados. El volumen 1, capítulo VI, da cuenta de las transformaciones afines, la torsión y la teoría general de la geodesia afín. El volumen 2 da una serie de aplicaciones de conexiones afines a espacios homogéneos y variedades complejas , así como a otros temas variados.

Lumiste, Ülo (2001a) [1994], "Affine connection" , en Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics , EMS Press , ISBN 978-1-55608-010-4.
Lumiste, Ülo (2001b) [1994], "Conexiones en una variedad" , en Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics , EMS Press , ISBN 978-1-55608-010-4.

Dos artículos de Lumiste, dando condiciones precisas sobre mapas de transporte paralelo para que definan conexiones afines. También tratan la curvatura, la torsión y otros temas estándar desde una perspectiva clásica (paquete no principal).

Sharpe, RW (1997), Geometría diferencial: Generalización de Cartan del programa Erlangen de Klein , Springer-Verlag, Nueva York, ISBN 0-387-94732-9.

Esto completa algunos de los detalles históricos y proporciona un relato elemental más fácil de leer sobre las conexiones de Cartan en general. El Apéndice A aclara la relación entre la conexión principal y los puntos de vista del paralelismo absoluto. El Apéndice B cierra la brecha entre el modelo clásico "rodante" de conexiones afines y el moderno basado en paquetes principales y operadores diferenciales.

Languages

In other projects