Espacio vectorial - Vector space

En matemáticas , física e ingeniería , un espacio vectorial (también llamado espacio lineal ) es un conjunto de objetos llamados vectores , que se pueden sumar y multiplicar ("escalar") por números llamados escalares . Los escalares son a menudo números reales , pero algunos espacios vectoriales tienen una multiplicación escalar por números complejos o, generalmente, por un escalar de cualquier campo matemático . Las operaciones de suma de vectores y multiplicación escalar deben satisfacer ciertos requisitos, llamados axiomas vectoriales (enumerados a continuación en § Definición ). Para especificar si los escalares en un espacio vectorial particular son números reales o números complejos, a menudo se utilizan los términos espacio vectorial real y espacio vectorial complejo .

Ciertos conjuntos de vectores euclidianos son ejemplos comunes de un espacio vectorial. Representan cantidades físicas tales como fuerzas , donde se pueden sumar dos fuerzas cualesquiera del mismo tipo para producir una tercera, y la multiplicación de un vector de fuerza por un multiplicador real es otro vector de fuerza. De la misma manera (pero en un sentido más geométrico ), los vectores que representan desplazamientos en el plano o espacio tridimensional también forman espacios vectoriales. Los vectores en espacios vectoriales no necesariamente tienen que ser objetos en forma de flechas como aparecen en los ejemplos mencionados: los vectores se consideran objetos matemáticos abstractos con propiedades particulares, que en algunos casos pueden visualizarse como flechas.

Los espacios vectoriales son objeto de álgebra lineal y están bien caracterizados por su dimensión , que, en términos generales, especifica el número de direcciones independientes en el espacio. Los espacios vectoriales de dimensión infinita surgen naturalmente en el análisis matemático como espacios funcionales , cuyos vectores son funciones . Estos espacios vectoriales generalmente están dotados de alguna estructura adicional como una topología , lo que permite considerar cuestiones de proximidad y continuidad . Entre estas topologías, las que están definidas por una norma o producto interno son las más utilizadas (dotadas de una noción de distancia entre dos vectores). Este es particularmente el caso de los espacios de Banach y los espacios de Hilbert , que son fundamentales en el análisis matemático.

Históricamente, las primeras ideas que conducen a los espacios vectoriales se remontan a la geometría analítica , las matrices , los sistemas de ecuaciones lineales y los vectores euclidianos del siglo XVII . El tratamiento moderno, más abstracto, formulado por primera vez por Giuseppe Peano en 1888, abarca objetos más generales que el espacio euclidiano , pero gran parte de la teoría puede verse como una extensión de ideas geométricas clásicas como líneas , planos y sus análogos de dimensiones superiores.

Hoy en día, los espacios vectoriales se aplican en matemáticas , ciencias e ingeniería . Son la noción lineal-algebraica apropiada para tratar con sistemas de ecuaciones lineales . Ofrecen un marco para la expansión de Fourier , que se emplea en las rutinas de compresión de imágenes , y proporcionan un entorno que se puede utilizar para técnicas de solución de ecuaciones diferenciales parciales . Además, los espacios vectoriales proporcionan una forma abstracta y sin coordenadas de tratar con objetos geométricos y físicos como los tensores . Esto, a su vez, permite el examen de las propiedades locales de las variedades mediante técnicas de linealización. Los espacios vectoriales pueden generalizarse de varias formas, lo que lleva a nociones más avanzadas en geometría y álgebra abstracta .

Este artículo trata principalmente de espacios vectoriales de dimensión finita. Sin embargo, muchos de los principios también son válidos para espacios vectoriales de dimensión infinita.

Estructuras algebraicas
Tipo grupo Grupo Semigrupo  / Monoid Rack y quandle Cuasigrupo y bucle Grupo abeliano Magma Grupo de mentiras Teoría de grupos
Como un anillo Anillo Rng Semiring Anillo cercano Anillo conmutativo Dominio integral Campo Anillo de división Teoría del anillo
celosía -como Enrejado Semirredura Celosía complementada Orden total Heyting álgebra álgebra de Boole Mapa de celosías Teoría de la celosía
Como un módulo Módulo Grupo con operadores Espacio vectorial Álgebra lineal
Algebra- like Álgebra De asociación No asociativo Álgebra de composición Álgebra de mentiras Calificado Bialgebra
v t mi

Introducción y definición

Primero se describen dos ejemplos típicos de espacios vectoriales, luego se introduce la definición de espacios vectoriales.

Primer ejemplo: flechas en el plano

El primer ejemplo de un espacio vectorial consta de flechas en un plano fijo , comenzando en un punto fijo. Esto se usa en física para describir fuerzas o velocidades . Dadas dos flechas cualesquiera, v y w , el paralelogramo atravesado por estas dos flechas contiene una flecha diagonal que también comienza en el origen. Esta nueva flecha se llama la suma de las dos flechas y se denota v + w . En el caso especial de dos flechas en la misma línea, su suma es la flecha en esta línea cuya longitud es la suma o la diferencia de las longitudes, dependiendo de si las flechas tienen la misma dirección. Otra operación que se puede hacer con flechas es escalar: dado cualquier número real positivo a , la flecha que tiene la misma dirección que v , pero se dilata o encoge al multiplicar su longitud por a , se llama multiplicación de v por a . Se denota una v . Cuando a es negativo, a v se define como la flecha que apunta en la dirección opuesta.

A continuación se muestran algunos ejemplos: si a = 2 , el vector resultante a w tiene la misma dirección que w , pero se estira al doble de longitud de w (imagen de la derecha a continuación). De manera equivalente, 2 w es la suma w + w . Además, (−1) v = - v tiene la dirección opuesta y la misma longitud que v (el vector azul apunta hacia abajo en la imagen de la derecha).

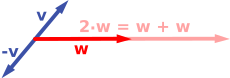
Segundo ejemplo: pares de números ordenados

Un segundo ejemplo clave de un espacio vectorial es proporcionado por pares de números reales x y y . (El orden de los componentes x y y es significativo, por lo que tal un par también se llama un par ordenado ). Tal un par se escribe como ( x , Y ) . La suma de dos de estos pares y la multiplicación de un par con un número se define de la siguiente manera:

${\ Displaystyle (x_ {1}, y_ {1}) + (x_ {2}, y_ {2}) = (x_ {1} + x_ {2}, y_ {1} + y_ {2})}$

y

${\ displaystyle a (x, y) = (ax, ay).}$

El primer ejemplo anterior se reduce a este ejemplo, si una flecha está representada por un par de coordenadas cartesianas de su punto final.

Definición

En este artículo, los vectores se representan en negrita para distinguirlos de los escalares.

Un espacio vectorial sobre un campo F es un conjunto  V junto con dos operaciones que satisfacen los ocho axiomas enumerados a continuación. A continuación, V × V denota el producto cartesiano de V consigo mismo, y → denota un mapeo de un conjunto a otro.

• La primera operación, denominada suma de vectores o simplemente Además +: V × V → V , toma dos vectores  v y w y les asigna un tercer vector que es comúnmente escrito como v + w , y llama la suma de estos dos vectores. (El vector resultante también es un elemento del conjunto V ).
• La segunda operación, denominada multiplicación escalar ·: F × V → V , toma cualquier escalar  una y cualquier vector  v y da otro vector  un v . (De manera similar, el vector de una v es un elemento del conjunto V . Multiplicación escalar es que no debe confundirse con el producto escalar , también llamado producto interno o producto escalar , que es una estructura adicional presente en algunos específicos, pero no todos los espacios vectoriales La multiplicación escalar es una multiplicación de un vector por un escalar; la otra es una multiplicación de dos vectores que producen un escalar.)

Los elementos de V se denominan comúnmente vectores . Los elementos de  F se denominan comúnmente escalares . Símbolos comunes para que denota espacios vectoriales incluyen U , V , y W .

En los dos ejemplos anteriores, el campo es el campo de los números reales y el conjunto de vectores consta de flechas planas con un punto de partida fijo y pares de números reales, respectivamente.

Para calificar como un espacio vectorial, el conjunto  V y las operaciones de suma vectorial y multiplicación escalar deben cumplir con una serie de requisitos llamados axiomas . Éstos se enumeran en la tabla siguiente, donde u , v y w denotan vectores arbitrarios en V , y un y b denotan escalares en F .

Axioma	Sentido
Asociatividad de la suma de vectores	u + ( v + w ) = ( u + v ) + w
Conmutatividad de la suma de vectores	u + v = v + u
Elemento de identidad de la suma de vectores	Existe un elemento 0 ∈ V , llamado el vector cero , de modo que v + 0 = v para todo v ∈ V .
Elementos inversos de la suma de vectores	Para cada v ∈ V , existe un elemento - v ∈ V , llamado inverso aditivo de v , tal que v + (- v ) = 0 .
Compatibilidad de la multiplicación escalar con la multiplicación de campos	a ( b v ) = ( ab ) v
Elemento de identidad de la multiplicación escalar	1 v = v , donde 1 indica la identidad multiplicativa en F .
Distributividad de la multiplicación escalar con respecto a la suma de vectores	a ( u + v ) = a u + a v
Distributividad de la multiplicación escalar con respecto a la suma de campos	( a + b ) v = a v + b v

Estos axiomas generalizan las propiedades de los vectores introducidos en los ejemplos anteriores. De hecho, el resultado de la suma de dos pares ordenados (como en el segundo ejemplo anterior) no depende del orden de los sumandos:

( x _v , y _v ) + ( x _w , y _w ) = ( x _w , y _w ) + ( x _v , y _v ) .

Asimismo, en el ejemplo geométrico de vectores como flechas, v + w = w + v ya que el paralelogramo que define la suma de los vectores es independiente del orden de los vectores. Todos los demás axiomas se pueden verificar de manera similar en ambos ejemplos. Así, al ignorar la naturaleza concreta del tipo particular de vectores, la definición incorpora estos dos y muchos más ejemplos en una noción de espacio vectorial.

La resta de dos vectores y la división por un escalar (distinto de cero) se puede definir como

${\ Displaystyle {\ begin {alineado} \ mathbf {v} - \ mathbf {w} & = \ mathbf {v} + (- \ mathbf {w}) \\ {\ frac {\ mathbf {v}} {a }} & = {\ frac {1} {a}} \ mathbf {v}. \ end {alineado}}}$

Cuando el campo escalar F son los números reales R , el espacio vectorial se denomina espacio vectorial real . Cuando el campo escalar son los números complejos C , el espacio vectorial se denomina espacio vectorial complejo . Estos dos casos son los que se utilizan con mayor frecuencia en ingeniería. La definición general de un espacio vectorial permite escalares sean elementos de cualquier fijo campo F . La noción es entonces conocido como un F - espacio vectorial o un espacio vectorial sobre F . Un campo es, esencialmente, un conjunto de números que poseen operaciones de suma , resta , multiplicación y división . Por ejemplo, los números racionales forman un campo.

En contraste con la intuición que surge de los vectores en el plano y los casos de dimensiones superiores, en los espacios vectoriales generales, no hay noción de cercanía , ángulos o distancias . Para tratar estos asuntos, se introducen tipos particulares de espacios vectoriales; consulte § Espacios vectoriales con estructura adicional a continuación para obtener más información.

Formulaciones alternativas y consecuencias elementales.

Además Vector y multiplicación escalar son operaciones, satisfaciendo el cierre de la propiedad: u + v y un v están en V para todos un en F , y u , v en V . Algunas fuentes más antiguas mencionan estas propiedades como axiomas separados.

En el lenguaje del álgebra abstracta , los primeros cuatro axiomas equivalen a requerir que el conjunto de vectores sea un grupo abeliano bajo adición. Los axiomas restantes dan a este grupo un F - módulo de estructura. En otras palabras, hay un homomorfismo de anillo f desde el campo F hacia el anillo de endomorfismo del grupo de vectores. Entonces la multiplicación escalar a v se define como ( f ( a )) ( v ) .

Hay una serie de consecuencias directas de los axiomas del espacio vectorial. Algunos de ellos derivan de la teoría de grupos elemental , aplicada al grupo aditivo de vectores: por ejemplo, el vector cero 0 de V y el aditivo inverso - v de cualquier vector v son únicos. Se siguen otras propiedades empleando también la ley distributiva para la multiplicación escalar, por ejemplo, a v es igual a 0 si y solo si a es igual a 0 o v es igual a 0 .

Historia

Los espacios vectoriales surgen de la geometría afín , mediante la introducción de coordenadas en el plano o espacio tridimensional. Alrededor de 1636, los matemáticos franceses René Descartes y Pierre de Fermat fundaron la geometría analítica identificando soluciones a una ecuación de dos variables con puntos en una curva plana . Para lograr soluciones geométricas sin utilizar coordenadas, Bolzano introdujo, en 1804, ciertas operaciones sobre puntos, líneas y planos, que son antecesores de los vectores. Möbius (1827) introdujo la noción de coordenadas baricéntricas . Bellavitis (1833) introdujo la noción de bipunto, es decir, un segmento orientado uno de cuyos extremos es el origen y el otro un objetivo. Los vectores fueron reconsiderados con la presentación de números complejos por Argand y Hamilton y el inicio de los cuaterniones por este último. Son elementos en R ² y R ⁴ ; tratarlos usando combinaciones lineales se remonta a Laguerre en 1867, quien también definió sistemas de ecuaciones lineales .

En 1857, Cayley introdujo la notación matricial que permite armonizar y simplificar los mapas lineales . Casi al mismo tiempo, Grassmann estudió el cálculo baricéntrico iniciado por Möbius. Imaginó conjuntos de objetos abstractos dotados de operaciones. En su trabajo están presentes los conceptos de independencia lineal y dimensión , así como productos escalares . En realidad, el trabajo de Grassmann de 1844 excede el marco de los espacios vectoriales, ya que su consideración de la multiplicación también lo llevó a lo que hoy se llama álgebras . El matemático italiano Peano fue el primero en dar la definición moderna de espacios vectoriales y mapas lineales en 1888.

Un desarrollo importante de los espacios vectoriales se debe a la construcción de espacios funcionales por Henri Lebesgue . Esto fue formalizado más tarde por Banach y Hilbert , alrededor de 1920. En ese momento, el álgebra y el nuevo campo del análisis funcional comenzaron a interactuar, en particular con conceptos clave como espacios de funciones integrables p y espacios de Hilbert . También en este momento, se realizaron los primeros estudios sobre espacios vectoriales de dimensión infinita.

Ejemplos de

Coordinar el espacio

El ejemplo más simple de un espacio vectorial sobre un campo F es el propio campo F (ya que es un grupo abeliano para la suma, una parte de los requisitos para ser un campo ), equipado con su suma (se convierte en suma vectorial) y multiplicación. (Se convierte en multiplicación escalar). De manera más general, todas las n- tuplas (secuencias de longitud n )

( un ₁ , un ₂ , ..., un _n )

de los elementos a _i de F forman un espacio vectorial que generalmente se denota F ⁿ y se llama espacio de coordenadas . El caso n = 1 es el ejemplo más simple mencionado anteriormente, en el que el campo F también se considera un espacio vectorial sobre sí mismo. El caso F = R y n = 2 (de modo R ² ) se discutió en la introducción anterior.

Números complejos y otras extensiones de campo

El conjunto de números complejos C , es decir, números que se pueden escribir en la forma x + iy para los números reales x y y donde i es la unidad imaginaria , forman un espacio vectorial sobre los reales con la adición y multiplicación habitual: ( x + iy ) + ( a + ib ) = ( x + a ) + i ( y + b ) y c ⋅ ( x + iy ) = ( c ⋅ x ) + i ( c ⋅ y ) para números reales x , y , un , b y c . Los diversos axiomas de un espacio vectorial se derivan del hecho de que las mismas reglas son válidas para la aritmética de números complejos.

De hecho, el ejemplo de números complejos es esencialmente el mismo que (es decir, es isomórfico a) el espacio vectorial de pares ordenados de números reales mencionado anteriormente: si pensamos en el número complejo x + i y como representando el par ordenado ( x , y ) en el plano complejo, entonces vemos que las reglas para la suma y la multiplicación escalar corresponden exactamente a las del ejemplo anterior.

Más en general, las extensiones de campo proporcionan otra clase de ejemplos de espacios vectoriales, particularmente en álgebra y teoría de números algebraica : un campo F que contiene un campo más pequeño E es un E espacio-vector, por las operaciones de multiplicación y suma dadas de F . Por ejemplo, los números complejos son un espacio vectorial sobre R , y la extensión de campo es un espacio vectorial sobre Q . ${\ Displaystyle \ mathbf {Q} (i {\ sqrt {5}})}$

Espacios funcionales

Las funciones de cualquier conjunto fijo Ω a un campo F también forman espacios vectoriales, al realizar la suma y la multiplicación escalar puntualmente. Es decir, la suma de dos funciones f y g es la función ( f + g ) dada por

( f + g ) ( w ) = f ( w ) + g ( w ) ,

y lo mismo para la multiplicación. Tales espacios de funciones se producen en muchas situaciones geométricas, cuando Ω es la recta real o un intervalo , o de otros subconjuntos de R . Muchas nociones en topología y análisis, como continuidad , integrabilidad o diferenciabilidad, se comportan bien con respecto a la linealidad: las sumas y los múltiplos escalares de funciones que poseen tal propiedad todavía tienen esa propiedad. Por tanto, el conjunto de tales funciones son espacios vectoriales. Se estudian con mayor detalle utilizando los métodos de análisis funcional , ver más abajo . Las restricciones algebraicas también producen espacios vectoriales: el espacio vectorial F [x] está dado por funciones polinómicas :

f ( x ) = r ₀ + r ₁ x + ... + r _{n -1} x ^{n -1} + r _n x ⁿ , donde los coeficientes r ₀ , ..., r _n están en F .

Ecuaciones lineales

Los sistemas de ecuaciones lineales homogéneas están estrechamente vinculados a los espacios vectoriales. Por ejemplo, las soluciones de

a	+	3 b	+	C	= 0
4 a	+	2 b	+	2 c	= 0

están dadas por triples con arbitrario a , b = a / 2 y c = −5 a / 2 . Forman un espacio vectorial: las sumas y los múltiplos escalares de tales triples aún satisfacen las mismas razones de las tres variables; por tanto, también son soluciones. Las matrices se pueden usar para condensar múltiples ecuaciones lineales como arriba en una ecuación vectorial, a saber

A x = 0 ,

donde es la matriz que contiene los coeficientes de las ecuaciones dadas, x es el vector ( a , b , c ) , A x denota el producto de la matriz y 0 = (0, 0) es el vector cero. De manera similar, las soluciones de ecuaciones diferenciales lineales homogéneas forman espacios vectoriales. Por ejemplo, ${\ displaystyle A = {\ begin {bmatrix} 1 & 3 & 1 \\ 4 & 2 & 2 \ end {bmatrix}}}$

f ′ ′ ( x ) + 2 f ′ ( x ) + f ( x ) = 0

los rendimientos de f ( x ) = a e ^{- x} + bx e ^{- x} , donde un y b son constantes arbitrarias, y e ^x es la función exponencial naturales .

Base y dimensión

Las bases permiten representar vectores mediante una secuencia de escalares llamados coordenadas o componentes . Una base es un conjunto B = { b _i } _{i ∈ I} de vectores b _i , por conveniencia, a menudo indexado por algún conjunto de índices I , que abarca todo el espacio y es linealmente independiente . "Abarcando todo el espacio" significa que cualquier vector v se puede expresar como una suma finita (llamada combinación lineal ) de los elementos básicos:

${\ Displaystyle \ mathbf {v} = a_ {1} \ mathbf {b} _ {i_ {1}} + a_ {2} \ mathbf {b} _ {i_ {2}} + \ cdots + a_ {n} \ mathbf {b} _ {i_ {n}},}$

( 1 )

donde la una _k son escalares, llamados las coordenadas (o los componentes) del vector v con respecto a la base B , y b _{i k} ( k = 1, ..., n ) elementos de B . La independencia lineal significa que las coordenadas a _k están determinadas de forma única para cualquier vector en el espacio vectorial.

Por ejemplo, los vectores de coordenadas e ₁ = (1, 0,…, 0) , e ₂ = (0, 1, 0,…, 0) , a e _n = (0, 0,…, 0, 1) , forman una base de F ⁿ , llamada base estándar , ya que cualquier vector ( x ₁ , x ₂ ,…, x _n ) se puede expresar de forma única como una combinación lineal de estos vectores:

( x ₁ , x ₂ ,…, x _n ) = x ₁ (1, 0,…, 0) + x ₂ (0, 1, 0,…, 0) + ⋯ + x _n (0,…, 0, 1) = x ₁ e ₁ + x ₂ e ₂ + ⋯ + x _n e _n .

Las coordenadas correspondientes x ₁ , x ₂ , … , x _n son solo las coordenadas cartesianas del vector.

Todo espacio vectorial tiene una base. Esto se sigue del lema de Zorn , una formulación equivalente del axioma de elección . Dados los otros axiomas de la teoría de conjuntos de Zermelo-Fraenkel , la existencia de bases es equivalente al axioma de elección. El lema del ultrafiltro , que es más débil que el axioma de elección, implica que todas las bases de un espacio vectorial dado tienen el mismo número de elementos o cardinalidad (cf. Teorema de dimensión para espacios vectoriales ). Se llama la dimensión del espacio vectorial, denotado por dim V . Si el espacio está atravesado por un número finito de vectores, las afirmaciones anteriores pueden probarse sin esa información fundamental de la teoría de conjuntos.

La dimensión del espacio de coordenadas F ⁿ es n , según la base mostrada anteriormente. La dimensión del anillo polinomial F [ x ] introducido anteriormente es numerablemente infinita , una base está dada por 1 , x , x ² , … A fortiori , la dimensión de espacios de funciones más generales, como el espacio de funciones en algunos (acotados o ilimitado) intervalo, es infinito. Bajo supuestos de regularidad adecuados sobre los coeficientes involucrados, la dimensión del espacio solución de una ecuación diferencial ordinaria homogénea es igual al grado de la ecuación. Por ejemplo, el espacio de solución para la ecuación anterior es generado por e ^{- x} y xe ^{- x} . Estas dos funciones son linealmente independientes sobre R , por lo que la dimensión de este espacio es dos, al igual que el grado de la ecuación.

Una extensión de campo sobre los racionales Q se puede considerar como un espacio vectorial sobre Q (definiendo la suma de vectores como suma de campo, definiendo la multiplicación escalar como multiplicación de campo por elementos de Q y, de lo contrario, ignorando la multiplicación de campo). La dimensión (o grado ) de la extensión de campo Q ( α ) sobre Q depende de α . Si α satisface alguna ecuación polinomial

con coeficientes racionales q _n , ..., q ₀ (es decir, si α es algebraico ), la dimensión es finita. Más precisamente, es igual al grado del polinomio mínimo que tiene α como raíz . Por ejemplo, los números complejos C son un espacio vectorial real bidimensional, generado por 1 y la unidad imaginaria i . Este último satisface i ² + 1 = 0, una ecuación de grado dos. Por tanto, C es un espacio de vectores R bidimensional (y, como cualquier campo, unidimensional como un espacio vectorial sobre sí mismo, C ). Si α no es algebraico, la dimensión de Q ( α ) sobre Q es infinita. Por ejemplo, para α = π no existe tal ecuación. Es decir, π es trascendental .

Matrices y mapas lineales

La relación de dos espacios vectoriales se puede expresar mediante mapa lineal o transformación lineal . Son funciones que reflejan la estructura del espacio vectorial, es decir, conservan sumas y multiplicaciones escalares:

${\ Displaystyle f (\ mathbf {v} + \ mathbf {w}) = f (\ mathbf {v}) + f (\ mathbf {w})}$y f ( un · v ) = un · f ( v ) para todos v y w en V , todo un en F .

Un isomorfismo es un mapa lineal f  : V → W tal que existe un mapa inverso g  : W → V , que es un mapa tal que las dos posibles composiciones f ∘ g  : W → W y g ∘ f  : V → V son mapas de identidad . De manera equivalente, f es tanto uno a uno ( inyectiva ) como sobre ( sobreyectiva ). Si existe un isomorfismo entre V y W , se dice que los dos espacios son isomorfos ; entonces son esencialmente idénticos a los espacios vectoriales, ya que todas las identidades que se mantienen en V son, a través de f , transportadas a otras similares en W , y viceversa a través de g .

Por ejemplo, los espacios vectoriales "flechas en el plano" y "pares ordenados de números" en la introducción son isomórficos: una flecha plana v que sale del origen de algún sistema de coordenadas (fijo) se puede expresar como un par ordenado considerando el x - y y componente z de la flecha, como se muestra en la imagen a la derecha. Por el contrario, dado un par ( x , y ) , la flecha que va por x hacia la derecha (o hacia la izquierda, si x es negativa), yy hacia arriba (hacia abajo, si y es negativa) hace retroceder la flecha v .

Los mapas lineales V → W entre dos espacios vectoriales forman un espacio vectorial Hom _F ( V , W ) , también denominado L ( V , W ) o 𝓛 ( V , W ) . El espacio de mapas lineales de V a F se llama espacio vectorial dual , denotado V ^∗ . A través del mapa natural inyectivo V → V ^∗∗ , cualquier espacio vectorial se puede incrustar en su bidual ; el mapa es un isomorfismo si y solo si el espacio es de dimensión finita.

Una vez que se elige una base de V , los mapas lineales f  : V → W se determinan completamente especificando las imágenes de los vectores base, porque cualquier elemento de V se expresa de forma única como una combinación lineal de ellos. Si dim V = dim W , una correspondencia 1-a-1 entre las bases fijas de V y W da lugar a un mapa lineal que mapea cualquier elemento base de V al elemento de base correspondiente de W . Es un isomorfismo, por su propia definición. Por lo tanto, dos espacios vectoriales son isomorfos si sus dimensiones coinciden y viceversa. Otra forma de expresar esto es que cualquier espacio vectorial está completamente clasificado ( hasta isomorfismo) por su dimensión, un solo número. En particular, cualquier espacio de n - vector F ndimensional V es isomorfo a F ⁿ . Sin embargo, no hay isomorfismo "canónico" o preferido; en realidad un isomorfismo φ  : F ⁿ → V es equivalente a la elección de una base de V , al mapear la base estándar de F ⁿ a V , a través de φ . La libertad de elegir una base conveniente es particularmente útil en el contexto de dimensión infinita; ver más abajo .

Matrices

Las matrices son una noción útil para codificar mapas lineales. Están escritos como una matriz rectangular de escalares como en la imagen de la derecha. Cualquier matriz A m -por- n da lugar a un mapa lineal de F ⁿ a F ^m , de la siguiente manera

${\ Displaystyle \ mathbf {x} = (x_ {1}, x_ {2}, \ ldots, x_ {n}) \ mapsto \ left (\ sum _ {j = 1} ^ {n} a_ {1j} x_ {j}, \ sum _ {j = 1} ^ {n} a_ {2j} x_ {j}, \ ldots, \ sum _ {j = 1} ^ {n} a_ {mj} x_ {j} \ right )}$, donde denota la suma ,${\ Displaystyle \ sum}$

o, usando la multiplicación matricial de la matriz A con el vector coordenado x :

x ↦ A x .

Además, después de elegir las bases de V y W , cualquier mapa lineal f  : V → W se representa de forma única mediante una matriz a través de esta asignación.

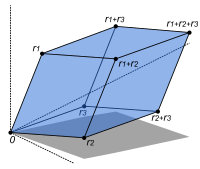
El determinante det ( A ) de una matriz cuadrada A es un escalar que dice si el mapa asociado es un isomorfismo o no: para serlo es suficiente y necesario que el determinante sea distinto de cero. La transformación lineal de R ⁿ correspondiente a una matriz real n- por- n conserva la orientación si y solo si su determinante es positivo.

Valores propios y vectores propios

Los endomorfismos , mapas lineales f  : V → V , son particularmente importantes ya que en este caso los vectores v se pueden comparar con su imagen bajo f , f ( v ) . Cualquier vector v distinto de cero que satisfaga λ v = f ( v ) , donde λ es un escalar, se denomina vector propio de f con valor propio λ . De manera equivalente, v es un elemento del núcleo de la diferencia f - λ · Id (donde Id es el mapa de identidad V → V ) . Si V es de dimensión finita, esto se puede reformular usando determinantes: f que tiene un valor propio λ es equivalente a

det ( f - λ · Id) = 0 .

Al deletrear la definición del determinante, se puede ver que la expresión del lado izquierdo es una función polinomial en λ , llamada polinomio característico de f . Si el campo F es lo suficientemente grande como para contener un cero de este polinomio (lo que ocurre automáticamente para F algebraicamente cerrado , como F = C ), cualquier mapa lineal tiene al menos un vector propio. El espacio vectorial V puede poseer o no una base propia , una base que consta de vectores propios. Este fenómeno se rige por la forma canónica del mapa de Jordania . El conjunto de todos los autovectores correspondientes a un autovalor particular de f forma un espacio vectorial conocido como el autoespacio correspondiente al autovalor ( yf ) en cuestión. Para lograr el teorema espectral , el enunciado correspondiente en el caso de dimensión infinita, se necesita la maquinaria del análisis funcional, ver más abajo .

Construcciones basicas

Además de los ejemplos concretos anteriores, hay una serie de construcciones algebraicas lineales estándar que producen espacios vectoriales relacionados con los dados. Además de las definiciones que se dan a continuación, también se caracterizan por propiedades universales , que determinan un objeto X especificando los mapas lineales de X a cualquier otro espacio vectorial.

Subespacios y espacios de cociente

Un subconjunto W no vacío de un espacio vectorial V que está cerrado bajo suma y multiplicación escalar (y por lo tanto contiene el vector 0 de V ) se llama subespacio lineal de V , o simplemente un subespacio de V , cuando el espacio ambiental es inequívocamente un espacio vectorial. Los subespacios de V son espacios vectoriales (sobre el mismo campo) por derecho propio. La intersección de todos los subespacios que contienen un conjunto dado S de vectores se llama su lapso , y es el subespacio más pequeño de V que contiene el conjunto S . Expresado en términos de elementos, el intervalo es el subespacio que consiste en todas las combinaciones lineales de los elementos de S .

Un subespacio lineal de dimensión 1 es una línea vectorial . Un subespacio lineal de dimensión 2 es un plano vectorial . Un subespacio lineal que contiene todos los elementos menos uno de la base del espacio ambiental es un hiperplano vectorial . En un espacio vectorial de dimensión finita n , un hiperplano vectorial es, por tanto, un subespacio de dimensión n - 1 .

La contraparte de los subespacios son los espacios vectoriales cocientes . Dado cualquier subespacio W ⊂ V , el espacio cociente V / W (" V módulo W ") se define de la siguiente manera: como un conjunto, consta de v + W = { v + w  : w ∈ W }, donde v es un vector arbitrario en V . La suma de dos de tales elementos v ₁ + W y v ₂ + W es ( v ₁ + v ₂ ) + W , y la multiplicación escalar es dada por un · ( v + W ) = ( un · v ) + W . El punto clave en esta definición es que v ₁ + W = v ₂ + W si y sólo si la diferencia de v ₁ y v ₂ mentiras en W . De esta manera, el espacio cociente de la información "olvida" que se contiene en el subespacio W .

El kernel ker ( f ) de un mapa lineal f  : V → W consta de vectores de v que se asignan a 0 en W . El núcleo y la imagen im ( f ) = { f ( v ): v ∈ V } son subespacios de V y W , respectivamente. La existencia de núcleos e imágenes es parte de la afirmación de que la categoría de espacios vectoriales (sobre un campo fijo F ) es una categoría abeliana , es decir, un corpus de objetos matemáticos y mapas que preservan la estructura entre ellos (una categoría ) que se comporta muy parecido a la categoría de grupos abelianos . Debido a esto, muchos enunciados, como el primer teorema del isomorfismo (también llamado teorema de nulidad de rango en términos relacionados con matrices)

V / ker ( f ) ≡ im ( f ).

y el teorema del segundo y tercer isomorfismo se puede formular y probar de una manera muy similar a los enunciados correspondientes para grupos .

Un ejemplo importante es el núcleo de un mapa lineal x ↦ A x para alguna matriz fija A , como se indicó anteriormente . El núcleo de este mapa es el subespacio de los vectores x tales que A x = 0 , que es precisamente el conjunto de soluciones al sistema de ecuaciones lineales homogéneos pertenecientes a A . Este concepto también se extiende a las ecuaciones diferenciales lineales.

${\ Displaystyle a_ {0} f + a_ {1} {\ frac {df} {dx}} + a_ {2} {\ frac {d ^ {2} f} {dx ^ {2}}} + \ cdots + a_ {n} {\ frac {d ^ {n} f} {dx ^ {n}}} = 0}$, donde los coeficientes a _{i también} son funciones en x .

En el mapa correspondiente

${\ Displaystyle f \ mapsto D (f) = \ sum _ {i = 0} ^ {n} a_ {i} {\ frac {d ^ {i} f} {dx ^ {i}}}}$,

las derivadas de la función f aparecen linealmente (a diferencia de f ′ ′ ( x ) ² , por ejemplo). Dado que la diferenciación es un procedimiento lineal (es decir, ( f + g ) ′ = f ′ + g ′ y ( c · f ) ′ = c · f ′ para una constante c ) esta asignación es lineal, llamada operador diferencial lineal . En particular, las soluciones de la ecuación diferencial D ( f ) = 0 forman un espacio vectorial (sobre R o C ).

Producto directo y suma directa

El producto directo de los espacios vectoriales y la suma directa de los espacios vectoriales son dos formas de combinar una familia indexada de espacios vectoriales en un nuevo espacio vectorial.

El producto directo de una familia de espacios vectoriales V _i consiste en el conjunto de todas las tuplas ( v _i ) _{i ∈ I} , que especifican para cada índice i en algún conjunto de índices I un elemento v _i de V _i . La suma y la multiplicación escalar se realizan por componentes. Una variante de esta construcción es la suma directa (también denominada coproducto y denotada ), donde solo se permiten tuplas con un número finito de vectores distintos de cero. Si el conjunto de índices I es finito, las dos construcciones concuerdan, pero en general son diferentes. ${\ Displaystyle \ textstyle {\ prod _ {i \ in I} V_ {i}}}$ ${\ textstyle \ bigoplus _ {i \ in I} V_ {i}}$${\ textstyle \ coprod _ {i \ in I} V_ {i}}$

Producto tensor

El producto tensorial V ⊗ _F W , o simplemente V ⊗ W , de dos espacios vectoriales V y W es una de las nociones centrales del álgebra multilineal que trata de extender nociones tales como mapas lineales a varias variables. Un mapa g  : V × W → X se llama bilineal si g es lineal en ambas variables v y w . Es decir, para w fijo el mapa v ↦ g ( v , w ) es lineal en el sentido anterior y también para v fijo .

El producto tensorial es un espacio vectorial particular que es un receptor universal de mapas bilineales g , como sigue. Se define como el espacio vectorial que consta de sumas finitas (formales) de símbolos llamados tensores.

v ₁ ⊗ w ₁ + v ₂ ⊗ w ₂ + ⋯ + v _n ⊗ w _n ,

sujeto a las reglas

a · ( v ⊗ w ) = ( a · v ) ⊗ w = v ⊗ ( a · w ), donde a es un escalar,

( v ₁ + v ₂ ) ⊗ w = v ₁ ⊗ w + v ₂ ⊗ w , y

v ⊗ ( w ₁ + w ₂ ) = v ⊗ w ₁ + v ⊗ w ₂ .

Estas reglas aseguran que el mapa f de V × W a V ⊗ W que asigna una tupla ( v , w ) a v ⊗ w sea ​​bilineal. La universalidad establece que dado cualquier espacio vectorial X y cualquier mapa bilineal g  : V × W → X , existe un mapa único u , que se muestra en el diagrama con una flecha punteada, cuya composición con f es igual a g : u ( v ⊗ w ) = g ( v , w ) . Esto se denomina propiedad universal del producto tensorial, una instancia del método, muy utilizado en álgebra abstracta avanzada, para definir indirectamente objetos mediante la especificación de mapas desde o hacia este objeto.

Espacios vectoriales con estructura adicional

Desde el punto de vista del álgebra lineal, los espacios vectoriales se entienden completamente en la medida en que cualquier espacio vectorial se caracteriza, hasta el isomorfismo, por su dimensión. Sin embargo, los espacios vectoriales por sí mismos no ofrecen un marco para abordar la cuestión, crucial para el análisis, de si una secuencia de funciones converge a otra función. Asimismo, el álgebra lineal no está adaptada para tratar con series infinitas , ya que la operación de suma solo permite sumar un número finito de términos. Por lo tanto, las necesidades del análisis funcional requieren considerar estructuras adicionales.

A un espacio vectorial se le puede dar un orden parcial ≤, bajo el cual se pueden comparar algunos vectores. Por ejemplo, el espacio real n- dimensional R ⁿ se puede ordenar comparando sus vectores en componentes. Los espacios vectoriales ordenados , por ejemplo los espacios de Riesz , son fundamentales para la integración de Lebesgue , que se basa en la capacidad de expresar una función como una diferencia de dos funciones positivas.

${\ Displaystyle f = f ^ {+} - f ^ {-}}$,

donde denota la parte positiva y la parte negativa. ${\ Displaystyle f ^ {+}}$${\ Displaystyle f}$${\ Displaystyle f ^ {-}}$

Espacios vectoriales normativos y espacios interiores de productos

La "medición" de vectores se realiza especificando una norma , un dato que mide las longitudes de los vectores, o mediante un producto interno , que mide los ángulos entre los vectores. Las normas y los productos internos se indican y , respectivamente. El dato de un producto interno implica que las longitudes de los vectores también se pueden definir, definiendo la norma asociada . Los espacios vectoriales dotados de tales datos se conocen como espacios vectoriales normativos y espacios de productos internos , respectivamente. ${\ Displaystyle | \ mathbf {v} |}$${\ Displaystyle \ langle \ mathbf {v}, \ mathbf {w} \ rangle}$${\ estilo de texto | \ mathbf {v} |: = {\ sqrt {\ langle \ mathbf {v}, \ mathbf {v} \ rangle}}}$

El espacio de coordenadas F ⁿ se puede equipar con el producto escalar estándar :

${\ Displaystyle \ langle \ mathbf {x}, \ mathbf {y} \ rangle = \ mathbf {x} \ cdot \ mathbf {y} = x_ {1} y_ {1} + \ cdots + x_ {n} y_ { norte}.}$

En R ² , esto refleja la idea común de que el ángulo entre dos vectores x y y , por la ley de los cosenos :

${\ Displaystyle \ mathbf {x} \ cdot \ mathbf {y} = \ cos \ left (\ angle (\ mathbf {x}, \ mathbf {y}) \ right) \ cdot | \ mathbf {x} | \ cdot | \ mathbf {y} |.}$

Debido a esto, dos vectores satisfactorios se denominan ortogonales . En el espacio de Minkowski se utiliza una variante importante del producto escalar estándar : R ⁴ dotado del producto Lorentz ${\ Displaystyle \ langle \ mathbf {x}, \ mathbf {y} \ rangle = 0}$

${\ Displaystyle \ langle \ mathbf {x} | \ mathbf {y} \ rangle = x_ {1} y_ {1} + x_ {2} y_ {2} + x_ {3} y_ {3} -x_ {4} y_ {4}.}$

A diferencia del producto escalar estándar, no es positivo definido : también toma valores negativos, por ejemplo, para . Al señalar la cuarta coordenada, que corresponde al tiempo , en oposición a las tres dimensiones del espacio, resulta útil para el tratamiento matemático de la relatividad especial . ${\ Displaystyle \ langle \ mathbf {x} | \ mathbf {x} \ rangle}$${\ Displaystyle \ mathbf {x} = (0,0,0,1)}$

Espacios vectoriales topológicos

Las preguntas de convergencia se tratan considerando espacios vectoriales V que tienen una topología compatible , una estructura que permite hablar de elementos cercanos entre sí . Compatible aquí significa que la suma y la multiplicación escalar deben ser mapas continuos . Aproximadamente, si x y y en V , y una en F varían por una cantidad limitada, a continuación, también lo hacen x + y y una x . Para que tenga sentido especificar la cantidad de cambios escalares, el campo F también tiene que llevar una topología en este contexto; una opción común son los reales o los números complejos.

En tales espacios vectoriales topológicos se pueden considerar series de vectores. La suma infinita

${\ Displaystyle \ sum _ {i = 0} ^ {\ infty} f_ {i}}$

denota el límite de los correspondientes sumas parciales finitas de la secuencia ( f _i ) _{i ∈ N} de elementos de V . Por ejemplo, f _i podrían ser funciones (reales o complejas) pertenecientes a algún espacio funcional V , en cuyo caso la serie es una serie de funciones . El modo de convergencia de la serie depende de la topología impuesta al espacio funcional. En tales casos, la convergencia puntual y la convergencia uniforme son dos ejemplos destacados.

Una forma de asegurar la existencia de límites de ciertas series infinitas es restringir la atención a los espacios donde cualquier secuencia de Cauchy tiene un límite; tal espacio vectorial se llama completo . Aproximadamente, un espacio vectorial está completo siempre que contenga todos los límites necesarios. Por ejemplo, el espacio vectorial de polinomios en el intervalo unitario [0,1], equipado con la topología de convergencia uniforme no está completo porque cualquier función continua en [0,1] puede aproximarse uniformemente mediante una secuencia de polinomios, por el Teorema de aproximación de Weierstrass . Por el contrario, el espacio de todas las funciones continuas en [0,1] con la misma topología es completo. Una norma da lugar a una topología al definir que una secuencia de vectores v _n converge av si y solo si

${\ Displaystyle \ lim _ {n \ to \ infty} | \ mathbf {v} _ {n} - \ mathbf {v} | = 0.}$

Los espacios de Banach y Hilbert son espacios vectoriales topológicos completos cuyas topologías vienen dadas, respectivamente, por una norma y un producto interno. Su estudio, pieza clave del análisis funcional, se centra en los espacios vectoriales de dimensión infinita, ya que todas las normas sobre espacios vectoriales topológicos de dimensión finita dan lugar a la misma noción de convergencia. La imagen de la derecha muestra la equivalencia de la norma 1 y la norma ∞ en R ² : a medida que las "bolas" unitarias se encierran entre sí, una secuencia converge a cero en una norma si y solo si lo hace en la otra norma . En el caso de dimensión infinita, sin embargo, generalmente habrá topologías desiguales, lo que hace que el estudio de los espacios vectoriales topológicos sea más rico que el de los espacios vectoriales sin datos adicionales.

Desde un punto de vista conceptual, todas las nociones relacionadas con los espacios vectoriales topológicos deben coincidir con la topología. Por ejemplo, en lugar de considerar todos los mapas lineales (también llamados funcionales ) V → W , se requiere que los mapas entre espacios vectoriales topológicos sean continuos. En particular, el espacio dual (topológico) V ^∗ consta de funcionales continuos V → R (o hacia C ). El teorema fundamental de Hahn-Banach se ocupa de separar subespacios de espacios vectoriales topológicos apropiados mediante funcionales continuos.

Espacios banach

Los espacios de Banach , presentados por Stefan Banach , son espacios vectoriales normalizados completos.

Un primer ejemplo es el espacio vectorial que${\ Displaystyle \ ell ^ {p}}$ consta de vectores infinitos con entradas reales cuya -norma dada por ${\ Displaystyle \ mathbf {x} = \ left (x_ {1}, x_ {2}, \ ldots, x_ {n}, \ ldots \ right)}$${\ Displaystyle p}$ ${\ Displaystyle (1 \ leq {p} \ leq \ infty)}$

${\ Displaystyle \ left \ | \ mathbf {x} \ right \ | _ {p}: = \ left (\ sum _ {i} \ left \ vert x_ {i} \ right \ vert ^ {p} \ right) ^ {\ frac {1} {p}}}$para    y   .${\ Displaystyle p <\ infty}$${\ Displaystyle \ left \ | \ mathbf {x} \ right \ | _ {\ infty}: = \ sup _ {i} \ left | x_ {i} \ right |}$

Las topologías en el espacio de dimensión infinita no son equivalentes para diferentes . Por ejemplo, la secuencia de vectores , en la que están los primeros componentes y los siguientes , converge al vector cero para , pero no para : ${\ Displaystyle \ ell ^ {p}}$${\ Displaystyle p}$${\ Displaystyle \ mathbf {x} _ {n} = \ left (2 ^ {- n}, 2 ^ {- n}, \ ldots, 2 ^ {- n}, 0,0, \ ldots \ right)}$${\ Displaystyle 2 ^ {n}}$${\ Displaystyle 2 ^ {- n}}$${\ Displaystyle 0}$${\ Displaystyle p = \ infty}$${\ Displaystyle p = 1}$

${\ Displaystyle \ left \ Vert \ mathbf {x} _ {n} \ right \ Vert _ {_ {\ infty}} = \ sup (2 ^ {- n}, 0) = 2 ^ {- n} \ rightarrow 0}$, pero ${\ Displaystyle \ left \ Vert \ mathbf {x} _ {n} \ right \ Vert _ {1} = \ sum _ {i = 1} ^ {2 ^ {n}} 2 ^ {- n} = 2 ^ {n} \ cdot 2 ^ {- n} = 1.}$

Más generalmente que las secuencias de números reales, las funciones están dotadas de una norma que reemplaza la suma anterior por la integral de Lebesgue.${\ Displaystyle f \ colon \ Omega \ to \ mathbb {R}}$

${\ Displaystyle \ left \ Vert {f} \ right \ Vert _ {p}: = \ left (\ int _ {\ Omega} \ left \ vert {f} \ left (x \ right) \ right \ vert ^ { p} \, {d \ mu \ left (x \ right)} \ right) ^ {\ frac {1} {p}}.}$

El espacio de funciones integrables en un dominio dado (por ejemplo, un intervalo) que satisface y está equipado con esta norma se denomina espacios de Lebesgue , denotado . ${\ Displaystyle \ Omega}$${\ Displaystyle \ left \ Vert {f} \ right \ Vert _ {p} <\ infty}$${\ Displaystyle L ^ {\; \! p} \ left (\ Omega \ right)}$

Estos espacios están completos. (Si se usa la integral de Riemann en su lugar, el espacio no está completo, lo que puede verse como una justificación de la teoría de la integración de Lebesgue). Concretamente, esto significa que para cualquier secuencia de funciones integrables de Lebesgue      con , satisfacer la condición ${\ Displaystyle f_ {1}, f_ {2}, \ ldots, f_ {n}, \ ldots}$${\ Displaystyle \ left \ Vert {f} _ {n} \ right \ Vert _ {p} <\ infty}$

${\ Displaystyle \ lim _ {k, \ n \ to \ infty} \ int _ {\ Omega} \ left \ vert {f} _ {k} (x) - {f} _ {n} (x) \ right \ vert ^ {p} \, {d \ mu \ left (x \ right)} = 0}$

existe una función perteneciente al espacio vectorial tal que ${\ Displaystyle {f} \ left (x \ right)}$${\ Displaystyle L ^ {\; \! p} \ left (\ Omega \ right)}$

${\ Displaystyle \ lim _ {k \ to \ infty} \ int _ {\ Omega} \ left \ vert {f} \ left (x \ right) - {f} _ {k} \ left (x \ right) \ right \ vert ^ {p} \, {d \ mu \ left (x \ right)} = 0.}$

La imposición de condiciones de delimitación no solo en la función, sino también en sus derivadas conduce a espacios de Sobolev .

Espacios de Hilbert

Los espacios de productos interiores completos se conocen como espacios de Hilbert , en honor a David Hilbert . El espacio de Hilbert L ² (Ω), con el producto interno dado por

${\ Displaystyle \ langle f \, \ g \ rangle = \ int _ {\ Omega} f (x) {\ overline {g (x)}} \, dx,}$

donde denota el conjugado complejo de g ( x ), es un caso clave. ${\ Displaystyle {\ overline {g (x)}}}$

Por definición, en un espacio de Hilbert cualquier secuencia de Cauchy converge hasta un límite. Por el contrario, es igualmente crucial encontrar una secuencia de funciones f _n con propiedades deseables que se aproxime a una función límite dada. El análisis inicial, bajo la apariencia de la aproximación de Taylor , estableció una aproximación de funciones diferenciables f por polinomios. Según el teorema de Stone-Weierstrass , cada función continua en [ a , b ] puede aproximarse tanto como se desee mediante un polinomio. Una técnica de aproximación similar mediante funciones trigonométricas se denomina comúnmente expansión de Fourier y se aplica mucho en ingeniería, ver más abajo . De manera más general, y más conceptual, el teorema proporciona una descripción simple de qué "funciones básicas", o, en espacios abstractos de Hilbert, qué vectores básicos son suficientes para generar un espacio de Hilbert H , en el sentido de que el cierre de su tramo (es decir , combinaciones lineales finitas y límites de aquellas) es todo el espacio. Este conjunto de funciones se denomina base de H , su cardinalidad se conoce como dimensión espacial de Hilbert . El teorema no solo muestra funciones de base adecuadas como suficientes para propósitos de aproximación, sino que también, junto con el proceso de Gram-Schmidt , permite construir una base de vectores ortogonales . Tales bases ortogonales son la generalización espacial de Hilbert de los ejes de coordenadas en el espacio euclidiano de dimensión finita .

Las soluciones de varias ecuaciones diferenciales se pueden interpretar en términos de espacios de Hilbert. Por ejemplo, una gran cantidad de campos de la física y la ingeniería conducen a tales ecuaciones y, con frecuencia, se utilizan como funciones básicas soluciones con propiedades físicas particulares, a menudo ortogonales. Como ejemplo de la física, la ecuación de Schrödinger dependiente del tiempo en mecánica cuántica describe el cambio de propiedades físicas en el tiempo mediante una ecuación diferencial parcial , cuyas soluciones se denominan funciones de onda . Los valores definidos de propiedades físicas como la energía o el momento, corresponden a valores propios de un determinado operador diferencial (lineal) y las funciones de onda asociadas se denominan estados propios . El teorema espectral descompone un operador compacto lineal que actúa sobre funciones en términos de estas funciones propias y sus valores propios.

Álgebras sobre campos

Los espacios vectoriales generales no poseen una multiplicación entre vectores. Un espacio vectorial equipado con un operador bilineal adicional que define la multiplicación de dos vectores es un álgebra sobre un campo . Muchas álgebras provienen de funciones en algún objeto geométrico: dado que las funciones con valores en un campo dado se pueden multiplicar puntualmente, estas entidades forman álgebras. El teorema de Stone-Weierstrass, por ejemplo, se basa en álgebras de Banach, que son tanto espacios de Banach como álgebras.

El álgebra conmutativa hace un gran uso de anillos de polinomios en una o varias variables, introducidas anteriormente . Su multiplicación es tanto conmutativa como asociativa . Estos anillos y sus cocientes forman la base de la geometría algebraica , porque son anillos de funciones de objetos geométricos algebraicos .

Otro ejemplo cruciales son álgebras de Lie , que no son ni conmutativa ni asociativo, pero el caso de no ser así se ve limitado por las restricciones ( [ x , y ] denota el producto de x y y ):

• [ x , y ] = - [ y , x ] ( anticomutatividad ), y
• [ x , [ y , z ]] + [ y , [ z , x ]] + [ z , [ x , y ]] = 0 ( identidad de Jacobi ).

Los ejemplos incluyen el espacio vectorial de n- por- n matrices, con [ x , y ] = xy - yx , el conmutador de dos matrices, y R ³ , dotado del producto cruzado .

El álgebra tensorial T ( V ) es una forma formal de sumar productos a cualquier espacio vectorial V para obtener un álgebra. Como espacio vectorial, está dividido por símbolos, llamados tensores simples.

v ₁ ⊗ v ₂ ⊗ ⋯ ⊗ v _n , donde el grado n varía.

La multiplicación se da concatenando tales símbolos, imponiendo la ley distributiva bajo la suma y requiriendo que la multiplicación escalar conmute con el producto tensorial ⊗, de la misma manera que con el producto tensorial de dos espacios vectoriales introducidos anteriormente . En general, no existen relaciones entre v ₁ ⊗ v ₂ y v ₂ ⊗ v ₁ . Forzar dos de estos elementos a ser iguales conduce al álgebra simétrica , mientras que forzar v ₁ ⊗ v ₂ = - v ₂ ⊗ v ₁ produce el álgebra exterior .

Cuando un campo, F se indica explícitamente, un término común utilizado es F -álgebra.

Aplicaciones

Los espacios vectoriales tienen muchas aplicaciones, ya que ocurren con frecuencia en circunstancias comunes, es decir, donde están involucradas funciones con valores en algún campo. Proporcionan un marco para tratar problemas analíticos y geométricos, o se utilizan en la transformada de Fourier. Esta lista no es exhaustiva: existen muchas más aplicaciones, por ejemplo en optimización . El teorema minimax de la teoría de juegos que establece la existencia de una recompensa única cuando todos los jugadores juegan de manera óptima se puede formular y probar utilizando métodos de espacios vectoriales. La teoría de la representación transfiere de manera fructífera la buena comprensión del álgebra lineal y los espacios vectoriales a otros dominios matemáticos, como la teoría de grupos .

Distribuciones

Una distribución (o función generalizada ) es un mapa lineal que asigna un número a cada función de "prueba" , típicamente una función suave con soporte compacto , de manera continua: en la terminología anterior , el espacio de distribuciones es el dual (continuo) de la espacio de función de prueba. Este último espacio está dotado de una topología que tiene en cuenta no solo f en sí mismo, sino también todas sus derivadas superiores. Un ejemplo estándar es el resultado de integrar una función de prueba f sobre algún dominio Ω:

${\ Displaystyle I (f) = \ int _ {\ Omega} f (x) \, dx.}$

Cuando Ω = { p } , el conjunto que consta de un solo punto, esto se reduce a la distribución de Dirac , denotada por δ , que asocia a una función de prueba f su valor en el p : δ ( f ) = f ( p ) . Las distribuciones son un poderoso instrumento para resolver ecuaciones diferenciales. Dado que todas las nociones analíticas estándar, como las derivadas, son lineales, se extienden naturalmente al espacio de distribuciones. Por lo tanto, la ecuación en cuestión se puede transferir a un espacio de distribución, que es más grande que el espacio funcional subyacente, de modo que se disponga de métodos más flexibles para resolver la ecuación. Por ejemplo, las funciones y soluciones fundamentales de Green suelen ser distribuciones en lugar de funciones propias, y luego se pueden usar para encontrar soluciones de la ecuación con condiciones de contorno prescritas. Entonces, en algunos casos, se puede demostrar que la solución encontrada es en realidad una función verdadera y una solución a la ecuación original (por ejemplo, utilizando el teorema de Lax-Milgram , una consecuencia del teorema de representación de Riesz ).

análisis de Fourier

La resolución de una función periódica en una suma de funciones trigonométricas forma una serie de Fourier , una técnica muy utilizada en física e ingeniería. El espacio vectorial subyacente suele ser el espacio de Hilbert L ² (0, 2π), para el cual las funciones sen ( mx ) y cos ( mx ) (donde m es un número entero) forman una base ortogonal. La expansión de Fourier de una función L ² f es

${\ Displaystyle {\ frac {a_ {0}} {2}} + \ sum _ {m = 1} ^ {\ infty} \ left [a_ {m} \ cos \ left (mx \ right) + b_ {m } \ sin \ left (mx \ right) \ right].}$

Los coeficientes a _m y b _m se denominan coeficientes de Fourier de f , y se calculan mediante las fórmulas

${\ Displaystyle a_ {m} = {\ frac {1} {\ pi}} \ int _ {0} ^ {2 \ pi} f (t) \ cos (mt) \, dt}$, ${\ Displaystyle b_ {m} = {\ frac {1} {\ pi}} \ int _ {0} ^ {2 \ pi} f (t) \ sin (mt) \, dt.}$

En términos físicos, la función se representa como una superposición de ondas sinusoidales y los coeficientes dan información sobre el espectro de frecuencias de la función . También se usa comúnmente una forma de número complejo de la serie de Fourier. Las fórmulas concretas anteriores son consecuencia de una dualidad matemática más general llamada dualidad de Pontryagin . Aplicado al grupo R , produce la transformada de Fourier clásica; una aplicación en física son las celosías recíprocas , donde el grupo subyacente es un espacio vectorial real de dimensión finita dotado con el dato adicional de una celosía que codifica las posiciones de los átomos en los cristales .

Las series de Fourier se utilizan para resolver problemas de valores en la frontera en ecuaciones diferenciales parciales . En 1822, Fourier utilizó por primera vez esta técnica para resolver la ecuación del calor . Se puede usar una versión discreta de la serie de Fourier en aplicaciones de muestreo donde el valor de la función se conoce solo en un número finito de puntos igualmente espaciados. En este caso, la serie de Fourier es finita y su valor es igual a los valores muestreados en todos los puntos. El conjunto de coeficientes se conoce como la transformada discreta de Fourier (DFT) de la secuencia de muestra dada. La DFT es una de las herramientas clave del procesamiento de señales digitales , un campo cuyas aplicaciones incluyen radar , codificación de voz , compresión de imágenes . El formato de imagen JPEG es una aplicación de la transformada de coseno discreta estrechamente relacionada .

La transformada rápida de Fourier es un algoritmo para calcular rápidamente la transformada discreta de Fourier. Se usa no solo para calcular los coeficientes de Fourier sino, usando el teorema de convolución , también para calcular la convolución de dos secuencias finitas. A su vez, se aplican en filtros digitales y como un algoritmo de multiplicación rápida para polinomios y números enteros grandes ( algoritmo de Schönhage-Strassen ).

Geometría diferencial

El plano tangente a una superficie en un punto es, naturalmente, un espacio vectorial cuyo origen se identifica con el punto de contacto. El plano tangente es la mejor aproximación lineal , o linealización , de una superficie en un punto. Incluso en un espacio euclidiano tridimensional, normalmente no existe una forma natural de prescribir una base del plano tangente, por lo que se concibe como un espacio vectorial abstracto en lugar de un espacio de coordenadas real. El espacio tangente es la generalización a variedades diferenciables de dimensiones superiores .

Las variedades de Riemann son variedades cuyos espacios tangentes están dotados de un producto interior adecuado . Derivado de allí, el tensor de curvatura de Riemann codifica todas las curvaturas de una variedad en un objeto, que encuentra aplicaciones en la relatividad general , por ejemplo, donde el tensor de curvatura de Einstein describe el contenido de materia y energía del espacio-tiempo . Al espacio tangente de un grupo de Lie se le puede dar naturalmente la estructura de un álgebra de Lie y se puede usar para clasificar grupos de Lie compactos .

Generalizaciones

Paquetes de vectores

Un paquete del vector es una familia de espacios vectoriales parametrizados continuamente por un espacio topológico X . Más precisamente, un paquete de vectores sobre X es un espacio topológico E equipado con un mapa continuo

π: E → X

tal que para cada x en X , la fibra π ⁻¹ ( x ) es un espacio vectorial. El caso dim V = 1 se llama paquete de líneas . Para cualquier espacio vectorial V , la proyección X × V → X convierte el producto X × V en un paquete de vectores "trivial" . Se requiere que los paquetes de vectores sobre X sean localmente un producto de X y algún espacio vectorial (fijo) V : para cada x en X , hay una vecindad U de x tal que la restricción de π a π ⁻¹ ( U ) es isomórfica al haz trivial U × V → U . A pesar de su carácter localmente trivial, los paquetes de vectores pueden (dependiendo de la forma del espacio subyacente X ) estar "retorcidos" en el gran (es decir, el paquete no necesita ser (globalmente isomórfico) el paquete trivial X × V ). Por ejemplo, la tira de Möbius se puede ver como un paquete de líneas sobre el círculo S ¹ ( identificando los intervalos abiertos con la línea real ). Sin embargo, es diferente del cilindro S ¹ × R , porque este último es orientable mientras que el primero no lo es.

Las propiedades de ciertos paquetes de vectores proporcionan información sobre el espacio topológico subyacente. Por ejemplo, el paquete tangente consiste en la colección de espacios tangentes parametrizados por los puntos de una variedad diferenciable. El haz tangente del círculo S ¹ es globalmente isomorfo a S ¹ × R , ya que hay un campo vectorial global distinto de cero en S ¹ . Por el contrario, según el teorema de la bola peluda , no hay un campo vectorial (tangente) en la 2-esfera S ² que es en todas partes distinto de cero. La teoría K estudia las clases de isomorfismo de todos los paquetes de vectores en algún espacio topológico. Además de profundizar visión topológica y geométrica, tiene consecuencias puramente algebraicas, tales como la clasificación de bienes de dimensión finita álgebra de división : R , C , la cuaterniones H y la octoniones O .

El haz cotangente de una variedad diferenciable consiste, en cada punto de la variedad, del dual del espacio tangente, el espacio cotangente . Las secciones de ese paquete se conocen como formas diferenciales uniformes .

Módulos

Los módulos son para los anillos lo que los espacios vectoriales son para los campos: los mismos axiomas, aplicados a un anillo R en lugar de un campo F , producen módulos. La teoría de los módulos, comparada con la de los espacios vectoriales, se complica por la presencia de elementos de anillo que no tienen inversos multiplicativos . Por ejemplo, los módulos no necesitan tener bases, como muestra el módulo Z (es decir, el grupo abeliano ) Z / 2 Z ; los módulos que lo hacen (incluidos todos los espacios vectoriales) se conocen como módulos libres . Sin embargo, un espacio vectorial puede definirse de manera compacta como un módulo sobre un anillo que es un campo , y los elementos se denominan vectores. Algunos autores utilizan el término espacio vectorial para referirse a módulos sobre un anillo de división . La interpretación algebro-geométrica de anillos conmutativos a través de su espectro permite el desarrollo de conceptos tales como módulos libres localmente , la contraparte algebraica de los paquetes de vectores.

Espacios afines y proyectivos

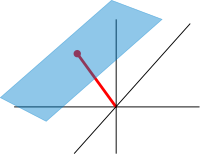
A grandes rasgos, los espacios afines son espacios vectoriales cuyos orígenes no se especifican. Más precisamente, un espacio afín es un conjunto con una acción de espacio vectorial transitiva libre . En particular, un espacio vectorial es un espacio afín sobre sí mismo, por el mapa

V × V → V , ( v , a ) ↦ a + v .

Si W es un espacio vectorial, entonces un subespacio afín es un subconjunto de W obtenido al traducir un subespacio lineal V por un vector fijo x ∈ W ; este espacio se denota por x + V (que es una clase lateral de V en W ) y consta de todos los vectores de la forma x + v para v ∈ V . Un ejemplo importante es el espacio de soluciones de un sistema de ecuaciones lineales no homogéneas.

A x = b

generalizando el caso homogéneo anterior , que se puede encontrar estableciendo b = 0 en esta ecuación. El espacio de soluciones es el subespacio afín x + V donde x es una solución particular de la ecuación y V es el espacio de soluciones de la ecuación homogénea (el espacio nulo de A ).

El conjunto de subespacios unidimensionales de un espacio vectorial V fijo de dimensión finita se conoce como espacio proyectivo ; puede usarse para formalizar la idea de líneas paralelas que se cruzan en el infinito. Grassmannianos y variedades de bandera generalizan esto parametrizando subespacios lineales de dimensión fija k y banderas de subespacios, respectivamente.

Ver también

• Vector (matemáticas y física) , para obtener una lista de varios tipos de vectores

Notas

Citas

Referencias

Álgebra

• Artin, Michael (1991), Álgebra , Prentice Hall , ISBN 978-0-89871-510-1
• Blass, Andreas (1984), "La existencia de bases implica el axioma de elección", Teoría de conjuntos axiomáticos (Boulder, Colorado, 1983) (PDF) , Contemporary Mathematics, 31 , Providence, RI: American Mathematical Society , pp. 31-33 , MR  0763890
• Brown, William A. (1991), Matrices and vector spaces , Nueva York: M. Dekker, ISBN 978-0-8247-8419-5
• Lang, Serge (1987), Álgebra lineal , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-96412-6
• Lang, Serge (2002), Álgebra , Textos de posgrado en matemáticas , 211 (Tercera edición revisada), Nueva York: Springer-Verlag, ISBN 978-0-387-95385-4, Señor  1878556
• Mac Lane, Saunders (1999), Álgebra (3ª ed.), Págs. 193–222, ISBN 978-0-8218-1646-2
• Meyer, Carl D. (2000), Análisis de matrices y álgebra lineal aplicada , SIAM , ISBN 978-0-89871-454-8
• Roman, Steven (2005), Álgebra lineal avanzada , Textos de posgrado en matemáticas, 135 (2a ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-24766-3
• Spindler, Karlheinz (1993), Álgebra abstracta con aplicaciones: Volumen 1: Espacios vectoriales y grupos , CRC, ISBN 978-0-8247-9144-5
• van der Waerden, Bartel Leendert (1993), Álgebra (en alemán) (9a ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-56799-8

Análisis

• Bourbaki, Nicolas (1987), Espacios vectoriales topológicos , Elementos de las matemáticas, Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-13627-9
• Bourbaki, Nicolas (2004), Integration I , Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-41129-1
• Braun, Martin (1993), Ecuaciones diferenciales y sus aplicaciones: una introducción a las matemáticas aplicadas , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-97894-9
• BSE-3 (2001) [1994], "Plano tangente" , Enciclopedia de Matemáticas , EMS Press
• Choquet, Gustave (1966), Topología , Boston, MA: Academic Press
• Dennery, Philippe; Krzywicki, Andre (1996), Matemáticas para físicos , Publicaciones de Courier Dover, ISBN 978-0-486-69193-0
• Dudley, Richard M. (1989), Análisis real y probabilidad , The Wadsworth & Brooks / Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks / Cole Advanced Books & Software, ISBN 978-0-534-10050-6
• Dunham, William (2005), The Calculus Gallery , Princeton University Press , ISBN 978-0-691-09565-3
• Evans, Lawrence C. (1998), ecuaciones diferenciales parciales , Providence, RI: American Mathematical Society , ISBN 978-0-8218-0772-9
• Folland, Gerald B. (1992), Análisis de Fourier y sus aplicaciones , Brooks-Cole, ISBN 978-0-534-17094-3
• Gasquet, Claude; Witomski, Patrick (1999), Análisis y aplicaciones de Fourier: filtrado, computación numérica, wavelets , textos en matemáticas aplicadas, Nueva York: Springer-Verlag, ISBN 978-0-387-98485-8
• Ifeachor, Emmanuel C .; Jervis, Barrie W. (2001), Procesamiento de señales digitales: un enfoque práctico (2a ed.), Harlow, Essex, Inglaterra: Prentice-Hall (publicado en 2002), ISBN 978-0-201-59619-9
• Krantz, Steven G. (1999), Panorama of Harmonic Analysis , Carus Mathematical Monographs, Washington, DC: Asociación Matemática de América, ISBN 978-0-88385-031-2
• Kreyszig, Erwin (1988), Matemáticas de ingeniería avanzada (6a ed.), Nueva York: John Wiley & Sons, ISBN 978-0-471-85824-9
• Kreyszig, Erwin (1989), Análisis funcional introductorio con aplicaciones , Wiley Classics Library, Nueva York: John Wiley & Sons , ISBN 978-0-471-50459-7, MR  0992618
• Lang, Serge (1983), Análisis real , Addison-Wesley , ISBN 978-0-201-14179-5
• Lang, Serge (1993), Análisis real y funcional , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-94001-4
• Loomis, Lynn H. (1953), Introducción al análisis armónico abstracto , Toronto-Nueva York-Londres: D. Van Nostrand Company, Inc., págs. X + 190, hdl : 2027 / uc1.b4250788
• Narici, Lawrence ; Beckenstein, Edward (2011). Espacios vectoriales topológicos . Matemáticas puras y aplicadas (Segunda ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC  144216834 .
• Schaefer, Helmut H .; Wolff, Manfred P. (1999). Espacios vectoriales topológicos . GTM . 8 (Segunda ed.). Nueva York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC  840278135 .
• Treves, François (1967), Espacios vectoriales topológicos, distribuciones y núcleos , Boston, MA: Academic Press

Referencias históricas

• Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (Sobre operaciones en conjuntos abstractos y su aplicación a ecuaciones integrales)" (PDF) , Fundamenta Mathematicae (en francés), 3 : 133– 181, doi : 10.4064 / fm-3-1-133-181 , ISSN  0016-2736
• Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Consideraciones sobre algunos aspectos de la geometría elemental) (en alemán)
• Bellavitis, Giuso (1833), "Sopra alcune Applicazioni di un nuovo metodo di geometria analitica", Il poligrafo giornale di scienze, lettre ed arti , Verona, 13 : 53–61.
• Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elementos de la historia de las matemáticas) (en francés), París: Hermann
• Dorier, Jean-Luc (1995), "Un esquema general de la génesis de la teoría del espacio vectorial" , Historia Mathematica , 22 (3): 227-261, doi : 10.1006 / hmat.1995.1024 , MR  1347828
• Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur (en francés), Chez Firmin Didot, père et fils
• Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik (en alemán), O. Wigand, reimpresión: Grassmann, Hermann (2000), Kannenberg, LC (ed.), Extension Theory , traducido por Kannenberg, Lloyd C., Providence, RI: American Mathematical Society , ISBN 978-0-8218-2031-5
• Hamilton, William Rowan (1853), Conferencias sobre cuaterniones , Real Academia Irlandesa
• Möbius, August Ferdinand (1827), Der Barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Cálculo baricéntrico: una nueva utilidad para un tratamiento analítico de la geometría) (en alemán), archivado desde el original el 23 de noviembre de 2006
• Moore, Gregory H. (1995), "La axiomatización del álgebra lineal: 1875-1940", Historia Mathematica , 22 (3): 262-303, doi : 10.1006 / hmat.1995.1025
• Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann precedeuto dalle Operazioni della Logica Deduttiva (en italiano), Turín
• Peano, G. (1901) Formulario matemático : axiomas vct vía Internet Archive

Otras referencias

• Ashcroft, Neil ; Mermin, N. David (1976), Física del estado sólido , Toronto: Thomson Learning, ISBN 978-0-03-083993-1
• Atiyah, Michael Francis (1989), teoría K , Advanced Book Classics (2a ed.), Addison-Wesley , ISBN 978-0-201-09394-0, MR  1043170
• Bourbaki, Nicolas (1998), Elements of Mathematics: Algebra I Chapters 1-3 , Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-64243-5
• Bourbaki, Nicolas (1989), Topología general. Capítulos 1-4 , Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-64241-1
• Coxeter, Harold Scott MacDonald (1987), Geometría proyectiva (2a ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-96532-1
• Eisenberg, Murray; Guy, Robert (1979), "Una prueba del teorema de la bola peluda", The American Mathematical Monthly , 86 (7): 572–574, doi : 10.2307 / 2320587 , JSTOR  2320587
• Eisenbud, David (1995), álgebra conmutativa , Textos de posgrado en matemáticas, 150 , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-94269-8, MR  1322960
• Goldrei, Derek (1996), Teoría de conjuntos clásica: un estudio independiente guiado (1ª ed.), Londres: Chapman y Hall , ISBN 978-0-412-60610-6
• Griffiths, David J. (1995), Introducción a la mecánica cuántica , Upper Saddle River, Nueva Jersey: Prentice Hall , ISBN 978-0-13-124405-4
• Halmos, Paul R. (1974), Espacios vectoriales de dimensión finita , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-90093-3
• Halpern, James D. (junio de 1966), "Bases in Vector Spaces and the Axiom of Choice", Proceedings of the American Mathematical Society , 17 (3): 670–673, doi : 10.2307 / 2035388 , JSTOR  2035388
• Hughes-Hallett, Deborah; McCallum, William G .; Gleason, Andrew M. (2013), Cálculo: simple y multivariable (6 ed.), John Wiley & Sons , ISBN 978-0470-88861-2
• Husemoller, Dale (1994), Fiber Bundles (3.a ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-94087-8
• Jost, Jürgen (2005), Geometría y análisis geométrico de Riemann (4a ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-25907-7
• Kreyszig, Erwin (1991), Geometría diferencial , Nueva York: Publicaciones de Dover , págs. Xiv + 352, ISBN 978-0-486-66721-8
• Kreyszig, Erwin (1999), Matemáticas de ingeniería avanzada (8a ed.), Nueva York: John Wiley & Sons , ISBN 978-0-471-15496-9
• Luenberger, David (1997), Optimización por métodos de espacio vectorial , Nueva York: John Wiley & Sons , ISBN 978-0-471-18117-0
• Mac Lane, Saunders (1998), Categorías para el matemático que trabaja (2a ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-98403-2
• Misner, Charles W .; Thorne, Kip ; Wheeler, John Archibald (1973), Gravitación , WH Freeman, ISBN 978-0-7167-0344-0
• Naber, Gregory L. (2003), La geometría del espacio-tiempo de Minkowski , Nueva York: Dover Publications , ISBN 978-0-486-43235-9, MR  2044239
• Schönhage, A .; Strassen, Volker (1971), "Schnelle Multiplikation großer Zahlen (Multiplicación rápida de números grandes)", Computación (en alemán), 7 (3-4): 281-292, doi : 10.1007 / bf02242355 , ISSN  0010-485X , S2CID  9738629
• Spivak, Michael (1999), Una introducción completa a la geometría diferencial (volumen dos) , Houston, TX: Publish or Perish
• Stewart, Ian (1975), Teoría de Galois , Serie de matemáticas de Chapman y Hall , Londres: Chapman y Hall , ISBN 978-0-412-10800-6
• Varadarajan, VS (1974), grupos de Lie, álgebras de Lie y sus representaciones , Prentice Hall , ISBN 978-0-13-535732-3
• Wallace, GK (febrero de 1992), "El estándar de compresión de imágenes fijas JPEG" (PDF) , IEEE Transactions on Consumer Electronics , 38 (1): xviii – xxxiv, CiteSeerX  10.1.1.318.4292 , doi : 10.1109 / 30.125072 , ISSN  0098 -3063 , archivado desde el original (PDF) el 13 de enero de 2007 , consultado el 25 de octubre de 2017
• Weibel, Charles A. (1994). Introducción al álgebra homológica . Estudios de Cambridge en Matemáticas Avanzadas. 38 . Prensa de la Universidad de Cambridge. ISBN 978-0-521-55987-4. Señor  1269324 . OCLC  36131259 .

enlaces externos

• "Espacio vectorial" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]