Homografía - Homography

En geometría proyectiva , una homografía es un isomorfismo de espacios proyectivos , inducido por un isomorfismo de los espacios vectoriales de los que derivan los espacios proyectivos. Es una biyección que asigna líneas a líneas y, por lo tanto, una colineación . En general, algunas colinaciones no son homografías, pero el teorema fundamental de la geometría proyectiva afirma que no es así en el caso de espacios proyectivos reales de dimensión al menos dos. Los sinónimos incluyen proyectividad , transformación proyectiva y colineación proyectiva .

Históricamente, las homografías (y los espacios proyectivos) se han introducido para estudiar la perspectiva y las proyecciones en la geometría euclidiana , y el término homografía , que, etimológicamente, significa aproximadamente "dibujo similar", data de esta época. A finales del siglo XIX se introdujeron definiciones formales de espacios proyectivos, que se diferenciaban de ampliar los espacios euclidianos o afines añadiendo puntos en el infinito . El término "transformación proyectiva" se originó en estas construcciones abstractas. Estas construcciones se dividen en dos clases que han demostrado ser equivalentes. Un espacio proyectivo puede construirse como el conjunto de líneas de un espacio vectorial sobre un campo dado (la definición anterior se basa en esta versión); esta construcción facilita la definición de coordenadas proyectivas y permite utilizar las herramientas del álgebra lineal para el estudio de homografías. El enfoque alternativo consiste en definir el espacio proyectivo a través de un conjunto de axiomas, que no involucran explícitamente ningún campo ( geometría de incidencia , ver también geometría sintética ); en este contexto, las colinaciones son más fáciles de definir que las homografías, y las homografías se definen como colinaciones específicas, por lo que se denominan "colinaciones proyectivas".

En aras de la simplicidad, a menos que se indique lo contrario, se supone que los espacios proyectivos considerados en este artículo se definen sobre un campo (conmutativo) . De manera equivalente , se supone que el teorema del hexágono de Pappus y el teorema de Desargues son verdaderos. Una gran parte de los resultados siguen siendo verdaderos, o pueden generalizarse a geometrías proyectivas para las que estos teoremas no son válidos.

Motivación geométrica

Los puntos A, B, C, D y A ′, B ′, C ′, D ′ están relacionados por una perspectividad, que es una transformación proyectiva.

Históricamente, el concepto de homografía se había introducido para comprender, explicar y estudiar la perspectiva visual y, específicamente, la diferencia en la apariencia de dos objetos planos vistos desde diferentes puntos de vista.

En el espacio euclidiano tridimensional, una proyección central desde un punto O (el centro) sobre un plano P que no contiene O es el mapeo que envía un punto A a la intersección (si existe) de la línea OA y el plano. P . La proyección no está definido si el punto A pertenece al plano que pasa por O y paralela a P . La noción de espacio proyectivo se introdujo originalmente extendiendo el espacio euclidiano, es decir, mediante la adición de puntos en el infinito a ella, con el fin de definir la proyección para cada punto excepto O .

Dado otro plano Q , que no contiene O , la restricción a Q de la proyección anterior se llama perspectiva .

Con estas definiciones, una perspectividad es solo una función parcial , pero se convierte en una biyección si se extiende a espacios proyectivos. Por tanto, esta noción se define normalmente para espacios proyectivos. La noción también se generaliza fácilmente a espacios proyectivos de cualquier dimensión, sobre cualquier campo , de la siguiente manera:

Dados dos espacios proyectivas P y Q de dimensión n , un perspectivity es una biyección de P a Q que se puede obtener mediante la incorporación de P y Q en un espacio proyectivo R de dimensión n + 1 y la restricción a P un saliente central en Q .

Si f es una perspectividad de P a Q , yg una perspectiva de Q a P , con un centro diferente, entonces g ⋅ f es una homografía de P a sí misma, que se denomina colineación central , cuando la dimensión de P está en al menos dos. (ver § Colinaciones centrales a continuación y Perspectividad § Colinaciones en perspectiva ).

Originalmente, una homografía se definió como la composición de un número finito de perspectivas. Es parte del teorema fundamental de la geometría proyectiva (ver más abajo) que esta definición coincide con la definición más algebraica esbozada en la introducción y detallada a continuación.

Definición y expresión en coordenadas homogéneas.

Un espacio proyectivo P ( V ) de dimensión n sobre un campo K puede definirse como el conjunto de las líneas que atraviesan el origen en un K -espacio vectorial V de dimensión n + 1 . Si se ha fijado una base de V , un punto de V puede estar representado por un punto de K ⁿ⁺¹ . Un punto de P ( V ), que es una línea en V , puede representarse así mediante las coordenadas de cualquier punto distinto de cero de esta línea, que se denominan así coordenadas homogéneas del punto proyectivo. ${\ Displaystyle (x_ {0}, \ ldots, x_ {n})}$

Dados dos espacios proyectivos P ( V ) y P ( W ) de la misma dimensión, una homografía es un mapeo de P ( V ) a P ( W ), que es inducida por un isomorfismo de espacios vectoriales . Tal isomorfismo induce una biyección de P ( V ) a P ( W ), debido a la linealidad de f . Dos de estos isomorfismos, f y g , definen la misma homografía si y solo si hay un elemento a de K distinto de cero tal que g = af . ${\ Displaystyle f: V \ rightarrow W}$

Esto puede escribirse en términos de coordenadas homogéneas de la siguiente manera: Una homografía φ puede definirse mediante una matriz n +1 × n +1 no singular [ a _{i , j} ], denominada matriz de la homografía . Esta matriz se define hasta la multiplicación por un elemento no nulo de K . Las coordenadas homogéneas de un punto y las coordenadas de su imagen por φ están relacionadas por ${\ Displaystyle [x_ {0}: \ cdots: x_ {n}]}$ ${\ Displaystyle [y_ {0}: \ cdots: y_ {n}]}$

{\ Displaystyle {\ begin {alineado} y_ {0} & = a_ {0,0} x_ {0} + \ dots + a_ {0, n} x_ {n} \\ & \ vdots \\ y_ {n} & = a_ {n, 0} x_ {0} + \ dots + a_ {n, n} x_ {n}. \ end {alineado}}}

Cuando los espacios proyectivos se definen agregando puntos en el infinito a espacios afines (finalización proyectiva), las fórmulas precedentes se convierten, en coordenadas afines,

{\ Displaystyle {\ begin {alineado} y_ {1} & = {\ frac {a_ {1,0} + a_ {1,1} x_ {1} + \ dots + a_ {1, n} x_ {n} " } {a_ {0,0} + a_ {0,1} x_ {1} + \ dots + a_ {0, n} x_ {n}}} \\ & \ vdots \\ y_ {n} & = {\ frac {a_ {n, 0} + a_ {n, 1} x_ {1} + \ puntos + a_ {n, n} x_ {n}} {a_ {0,0} + a_ {0,1} x_ { 1} + \ puntos + a_ {0, n} x_ {n}}} \ end {alineado}}}

que generaliza la expresión de la función homográfica de la siguiente sección. Esto define solo una función parcial entre espacios afines, que se define solo fuera del hiperplano donde el denominador es cero.

Homografías de una línea proyectiva

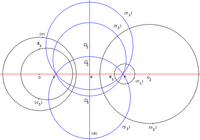
Las homografías del plano complejo conservan los círculos ortogonales.

La línea proyectiva sobre un campo K puede identificarse con la unión de K y un punto, llamado "punto en el infinito" y denotado por ∞ (ver línea proyectiva ). Con esta representación de la línea proyectiva, las homografías son los mapeos

{\ Displaystyle z \ mapsto {\ frac {az + b} {cz + d}}, {\ text {where}} ad-bc \ neq 0,}

que se denominan funciones homográficas o transformaciones fraccionarias lineales .

En el caso de la línea proyectiva compleja , que se puede identificar con la esfera de Riemann , las homografías se denominan transformaciones de Möbius . Estos se corresponden precisamente con aquellas biyecciones de la esfera de Riemann que conservan la orientación y son conformes.

En el estudio de las colinaciones, el caso de las líneas proyectivas es especial debido a la pequeña dimensión. Cuando la línea se ve como un espacio proyectivo de forma aislada, cualquier permutación de los puntos de una línea proyectiva es una colineación, ya que cada conjunto de puntos es colineal. Sin embargo, si la línea proyectiva está incrustada en un espacio proyectivo de mayor dimensión, la estructura geométrica de ese espacio puede usarse para imponer una estructura geométrica en la línea. Así, en geometría sintética, las homografías y las colinaciones de la línea proyectiva que se consideran son las obtenidas por restricciones a la línea de colinaciones y homografías de espacios de mayor dimensión. Esto significa que el teorema fundamental de la geometría proyectiva (ver más abajo) sigue siendo válido en el escenario unidimensional. Una homografía de una línea proyectiva también se puede definir correctamente insistiendo en que el mapeo conserva las relaciones cruzadas .

Marco proyectivo y coordenadas

Un marco proyectivo o base proyectiva de un espacio proyectivo de dimensión $n$ es un conjunto ordenado de $n + 2$ puntos de manera que ningún hiperplano contiene $n + 1$ de ellos. Un marco proyectivo a veces se llama simplex , aunque un simplex en un espacio de dimensión $n$ tiene como máximo $n + 1$ vértices.

Los espacios proyectivos sobre un campo conmutativo $K$ se consideran en esta sección, aunque la mayoría de los resultados pueden generalizarse a espacios proyectivos sobre un anillo de división .

Sea $P (V)$ un espacio proyectivo de dimensión $n$ , donde $V$ es un espacio de $K$ -vector de dimensión $n + 1$ , y sea la proyección canónica que mapea un vector distinto de cero a la línea vectorial que lo contiene. ${\ Displaystyle p: V \ setminus \ {0 \} \ to P (V)}$

Para cada trama de $P (V)$ , existe una base de $V$ de tal manera que el marco es y esta base es de hasta única para la multiplicación de todos sus elementos por el mismo elemento no nulo de $K$ . Por el contrario, si es una base de $V$ , entonces es una trama de $P$ $($ $V$ $)$ ${\ Displaystyle e_ {0}, \ dots, e_ {n}}$ ${\ Displaystyle \ left (p (e_ {0}), \ ldots, p (e_ {n}), p (e_ {0} + \ dots + e_ {n}) \ right),}$ ${\ Displaystyle e_ {0}, \ dots, e_ {n}}$ ${\ Displaystyle \ left (p (e_ {0}), \ ldots, p (e_ {n}), p (e_ {0} + \ dots + e_ {n}) \ right)}$

De ello se deduce que, dados dos fotogramas, hay exactamente una homografía que mapea el primero en el segundo. En particular, la única homografía que fija los puntos de un marco es el mapa de identidad . Este resultado es mucho más difícil en geometría sintética (donde los espacios proyectivos se definen a través de axiomas). A veces se le llama el primer teorema fundamental de la geometría proyectiva .

Cada cuadro permite definir coordenadas proyectivas , también conocidas como coordenadas homogéneas : cada punto puede escribirse como $p$ $($ $v$ $)$ ; las coordenadas proyectivas de $p$ $($ $v$ $)$ en este marco son las coordenadas de $v$ en la base No es difícil verificar que cambiar la y $v$ , sin cambiar el marco ni p ( v ), resulta en multiplicar las coordenadas proyectivas por el mismo elemento no nulo de K . ${\ Displaystyle (p (e_ {0}), \ ldots, p (e_ {n}), p (e_ {0} + \ cdots + e_ {n}))}$ ${\ Displaystyle (e_ {0}, \ ldots, e_ {n}).}$ ${\ Displaystyle e_ {i}}$

El espacio proyectivo $P n (K) = P (K n +1)$ tiene un marco canónico que consiste en la imagen por $p$ de la base canónica de $K n +1$ (que consiste en los elementos que tienen solo una entrada distinta de cero, que es igual a 1) y $(1, 1, ..., 1)$ . Sobre esta base, las coordenadas homogéneas de $p (v)$ son simplemente las entradas (coeficientes) de la tupla $v$ . Dado otro espacio proyectivo $P (V)$ de la misma dimensión, y un marco $F$ del mismo, hay una y solo una homografía $h$ mapeando $F$ en el marco canónico de $P n (K)$ . Las coordenadas proyectivas de un punto $a$ en el marco $F$ son las coordenadas homogéneas de $h (a)$ en el marco canónico de $P n (K)$ .

Colinaciones centrales

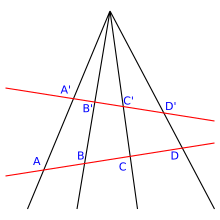
Los puntos A, B, C, D y A ′, B ′, C ′, D ′ están relacionados por varias colinaciones centrales, que se especifican completamente eligiendo una línea de puntos fijos L que pasa por la intersección de las líneas ABCD y A ′ B′C′D ′. Sea O la intersección de las líneas AA ′, BB ′, CC ′, DD ′. La imagen E ′ de un punto E por esta colineación es la intersección de las líneas A′I y OE, donde I es la intersección de las líneas L y AE.

En las secciones anteriores, las homografías se han definido mediante álgebra lineal. En geometría sintética , tradicionalmente se definen como la composición de una o varias homografías especiales llamadas colinaciones centrales . Es parte del teorema fundamental de la geometría proyectiva que las dos definiciones son equivalentes.

En un espacio proyectivo, P , de dimensión n ≥ 2 , una colineación de P es una biyección de P sobre P que mapea líneas sobre líneas. Una colineación central (tradicionalmente se llamaban perspectivas , pero este término puede ser confuso y tener otro significado; ver Perspectividad ) es una biyección α de P a P , de manera que existe un hiperplano H (llamado eje de α ), que es punto fijo por α (es decir, α ( X ) = X para todos los puntos X en H ) y un punto O (llamado el centro de α ), que está fijo en línea por α (cualquier línea que pasa por O se asigna a sí misma por α , pero no necesariamente puntual). Hay dos tipos de colinaciones centrales. Las elaciones son las colinaciones centrales en las que el centro incide con el eje y las homologías son aquellas en las que el centro no incide con el eje. Una colineación central se define de forma única por su centro, su eje y la imagen α ( P ) de cualquier punto P dado que difiera del centro O y no pertenezca al eje. (La imagen α ( Q ) de cualquier otro punto Q es la intersección de la línea definida por O y Q y la línea que pasa por α ( P ) y la intersección con el eje de la línea definida por P y Q ).

Una colineación central es una homografía definida por una matriz ( n +1) × ( n +1) que tiene un espacio propio de dimensión n . Es una homología, si la matriz tiene otro valor propio y, por lo tanto, es diagonalizable . Es una euforia, si todos los valores propios son iguales y la matriz no es diagonalizable.

La vista geométrica de una colineación central es más fácil de ver en un plano proyectivo. Dado un colineación α central, considerar una línea que no pasa a través del centro O , y su imagen bajo α , . Configuración , el eje de α es alguna línea M a través de R . La imagen de cualquier punto A de debajo de α es la intersección de OA con . La imagen B ′ de un punto B que no pertenece se puede construir de la siguiente manera: vamos , entonces . ${\ Displaystyle \ ell}$ ${\ Displaystyle \ ell '= \ alpha (\ ell)}$ ${\ Displaystyle R = \ ell \ cap \ ell '}$ ${\ Displaystyle \ ell}$ ${\ Displaystyle \ ell '}$ ${\ Displaystyle \ ell}$ ${\ Displaystyle S = AB \ cap M}$ ${\ displaystyle B '= SA' \ cap OB}$

La composición de dos colinaciones centrales, aunque sigue siendo una homografía en general, no es una colineación central. De hecho, toda homografía es la composición de un número finito de colinaciones centrales. En geometría sintética, esta propiedad, que forma parte de la teoría fundamental de la geometría proyectiva, se toma como definición de homografías.

Teorema fundamental de la geometría proyectiva

Hay colinaciones además de las homografías. En particular, cualquier automorfismo de campo σ de un campo F induce una colineación de cada espacio proyectivo sobre F aplicando σ a todas las coordenadas homogéneas (sobre un marco proyectivo) de un punto. Estas colinaciones se denominan colinaciones automórficas .

El teorema fundamental de la geometría proyectiva consta de los tres teoremas siguientes.

Dados dos marcos proyectivos de un espacio proyectivo P , hay exactamente una homografía de P que mapea el primer marco sobre el segundo.
Si la dimensión de un espacio proyectivo P es al menos dos, cada colineación de P es la composición de una colineación automórfica y una homografía. En particular, sobre los reales, cada colineación de un espacio proyectivo de dimensión al menos dos es una homografía.
Toda homografía es la composición de un número finito de perspectivas . En particular, si la dimensión del espacio proyectivo implícito es al menos dos, toda homografía es la composición de un número finito de colinaciones centrales.

Si los espacios proyectivos se definen mediante axiomas ( geometría sintética ), la tercera parte es simplemente una definición. Por otro lado, si los espacios proyectivos se definen mediante álgebra lineal , la primera parte es un corolario fácil de las definiciones. Por tanto, la prueba de la primera parte en geometría sintética y la prueba de la tercera parte en términos de álgebra lineal son pasos fundamentales de la prueba de la equivalencia de las dos formas de definir espacios proyectivos.

Grupos de homografía

Como toda homografía tiene un mapeo inverso y la composición de dos homografías es otra, las homografías de un espacio proyectivo dado forman un grupo . Por ejemplo, el grupo de Möbius es el grupo de homografía de cualquier línea proyectiva compleja.

Como todos los espacios proyectivos de la misma dimensión sobre el mismo campo son isomorfos, lo mismo ocurre con sus grupos de homografía. Por lo tanto, se consideran como un solo grupo que actúa sobre varios espacios, y solo la dimensión y el campo aparecen en la notación, no el espacio proyectivo específico.

Grupos homografía también llamados grupos lineales proyectivas se denotan PGL ( n + 1, F ) cuando actúa en un espacio proyectivo de dimensión n sobre un campo F . La definición anterior de homografías muestra que PGL ( n + 1, F ) puede identificarse con el grupo cociente GL ( n + 1, F ) / F ^× I , donde GL ( n + 1, F ) es el grupo lineal general del matrices invertibles , y F ^× I es el grupo de los productos por un elemento distinto de cero de F de la matriz identidad de tamaño ( n + 1) × ( n + 1) .

Cuando F es un campo de Galois GF ( q ), entonces el grupo de homografía se escribe PGL ( n , q ) . Por ejemplo, PGL (2, 7) actúa sobre los ocho puntos de la línea proyectiva sobre el campo finito GF (7), mientras que PGL (2, 4) , que es isomorfo al grupo alterno A ₅ , es el grupo de homografía de la línea proyectiva con cinco puntos.

El grupo de homografía PGL ( n + 1, F ) es un subgrupo del grupo de colineación PΓL ( n + 1, F ) de las colinaciones de un espacio proyectivo de dimensión n . Cuando los puntos y líneas del espacio proyectivo se ven como un diseño de bloque , cuyos bloques son los conjuntos de puntos contenidos en una línea, es común llamar al grupo de colineación el grupo de automorfismo del diseño .

Razón cruzada

Uso de relaciones cruzadas en geometría proyectiva para medir las dimensiones del mundo real de las características representadas en una proyección en perspectiva . A, B, C, D y V son puntos en la imagen, su separación se expresa en píxeles; A ', B', C 'y D' están en el mundo real, su separación en metros.

En (1), el ancho de la calle lateral, W se calcula a partir de los anchos conocidos de las tiendas adyacentes.
En (2), solo se necesita el ancho de una tienda porque un punto de fuga , V, es visible.

La relación cruzada de cuatro puntos colineales es una invariante bajo la homografía fundamental para el estudio de las homografías de las líneas.

Tres puntos distintos $a$ , $b$ y $c$ en una línea proyectiva sobre un campo $F$ forman un marco proyectivo de esta línea. Existe por tanto una homografía único $h$ de esta línea en $F \cup \infty$ que mapea $una$ a $\infty$ , $b$ a 0, y $c$ a 1. Dado un cuarto punto en la misma línea, la razón doble de los cuatro puntos $de una$ , $b$ , $c$ y $d$ , denotado $[un, b; c, d]$ , es el elemento $h (d)$ de $F \cup \infty$ . En otras palabras, si $d$ tiene coordenadas homogéneas $[k : 1]$ sobre el marco proyectivo $(a, b, c)$ , entonces $[a, b; c, d] = k$ .

Sobre un anillo

Suponga que A es un anillo y U es su grupo de unidades . Las homografías actúan sobre una línea proyectiva sobre A , escrita P ( A ), que consta de puntos U [ a, b ] con coordenadas proyectivas . Las homografías en P ( A ) se describen mediante mapeos matriciales

{\ Displaystyle U [z, 1] {\ begin {pmatrix} a & c \\ b & d \ end {pmatrix}} = U [za + b, \ zc + d].}

Cuando A es un anillo conmutativo , la homografía puede escribirse

{\ Displaystyle z \ mapsto {\ frac {za + b} {zc + d}} \,}

pero de lo contrario, la transformación fraccional lineal se considera una equivalencia:

{\ Displaystyle U [za + b, \ zc + d] \ thicksim U [(zc + d) ^ {- 1} (za + b), \ 1].}

El grupo de homografía del anillo de números enteros Z es el grupo modular PSL (2, Z ) . Se han utilizado homografías de anillo en el análisis de cuaterniones y con cuaterniones duales para facilitar la teoría de los tornillos . El grupo conforme del espacio-tiempo se puede representar con homografías donde A es el álgebra de composición de biquaternions .

Homografías periódicas

La homografía es periódica cuando el anillo es Z / n Z (los números enteros módulo n ), ya que Arthur Cayley estaba interesado en la periodicidad cuando calculó iteraciones en 1879. En su revisión de un enfoque de fuerza bruta para la periodicidad de las homografías, HSM Coxeter dio este análisis: ${\ displaystyle h = {\ begin {pmatrix} 1 & 1 \\ 0 & 1 \ end {pmatrix}}}$ ${\ displaystyle h ^ {n} = {\ begin {pmatrix} 1 & n \\ 0 & 1 \ end {pmatrix}} = {\ begin {pmatrix} 1 & 0 \\ 0 & 1 \ end {pmatrix}}.}$

Una homografía real es involutiva (del período 2) si y solo si a + d = 0 . Si es periódico con período n > 2 , entonces es elíptico y no se produce pérdida de generalidad asumiendo que ad - bc = 1 . Dado que las raíces características son exp (± hπi / m ), donde ( h , m ) = 1 , la traza es a + d = 2 cos ( hπ / m ) .

Ver también

Curva W

Notas

Referencias

Artin, E. (1957), Álgebra geométrica , Interscience Publishers
Baer, Reinhold (2005) [Publicado por primera vez en 1952], Álgebra lineal y geometría proyectiva , Dover, ISBN 9780486445656
Berger, Marcel (2009), Geometría I , Springer-Verlag, ISBN 978-3-540-11658-5 , traducido del original francés de 1977 por M. Cole y S. Levy, cuarta edición de la traducción inglesa de 1987
Beutelspacher, Albrecht; Rosenbaum, Ute (1998), Geometría proyectiva: de los fundamentos a las aplicaciones , Cambridge University Press, ISBN 0-521-48364-6
Hartshorne, Robin (1967), Fundamentos de la geometría proyectiva , Nueva York: WA Benjamin, Inc
Hirschfeld, JWP (1979), Geometrías proyectivas sobre campos finitos , Oxford University Press , ISBN 978-0-19-850295-1
Meserve, Bruce E. (1983), Conceptos fundamentales de geometría , Dover, ISBN 0-486-63415-9
Yale, Paul B. (1968), Geometría y simetría , Holden-Day

Otras lecturas

Patrick du Val (1964) Homografías, cuaterniones y rotaciones , Oxford Mathematical Monographs, Clarendon Press , Oxford , MR 0169108 .
Gunter Ewald (1971) Geometría: Introducción , página 263, Belmont: Wadsworth Publishing ISBN 0-534-00034-7 .

Languages

In other projects