Categoría monoidal - Monoidal category

En matemáticas , una categoría monoidal (o categoría tensorial ) es una categoría equipada con un bifunctor${\ Displaystyle \ mathbf {C}}$

${\ Displaystyle \ otimes: \ mathbf {C} \ times \ mathbf {C} \ to \ mathbf {C}}$

que es asociativo hasta un isomorfismo natural , y un objeto I que es tanto una identidad de izquierda como de derecha para ⊗, nuevamente hasta un isomorfismo natural. Los isomorfismos naturales asociados están sujetos a ciertas condiciones de coherencia , que aseguran que todos los diagramas relevantes conmuten .

La corriente de producto tensor hace que los espacios vectoriales , grupos abelianos , R -modules , o R -álgebras en categorías monoidales. Las categorías monoidales pueden verse como una generalización de estos y otros ejemplos. Cada categoría monoidal ( pequeña ) también puede verse como una " categorización " de un monoide subyacente , es decir, el monoide cuyos elementos son las clases de isomorfismo de los objetos de la categoría y cuya operación binaria viene dada por el producto tensorial de la categoría.

Una aplicación bastante diferente, de la cual las categorías monoidales pueden considerarse una abstracción, es la de un sistema de tipos de datos cerrados bajo un constructor de tipos que toma dos tipos y construye un tipo agregado; los tipos son los objetos y es el constructor agregado. La asociatividad hasta el isomorfismo es entonces una forma de expresar que diferentes formas de agregar los mismos datos, como y, almacenan la misma información, aunque los valores agregados no tienen por qué ser los mismos. El tipo agregado puede ser análogo a la operación de suma (tipo suma) o de multiplicación (tipo producto). Para el producto de tipo, el objeto de identidad es la unidad , por lo que solo hay un habitante del tipo, y es por eso que un producto con él siempre es isomorfo al otro operando. Para el tipo suma, el objeto de identidad es el tipo vacío , que no almacena información y es imposible dirigirse a un habitante. El concepto de categoría monoidal no presupone que los valores de tales tipos de agregados puedan separarse; por el contrario, proporciona un marco que unifica la teoría de la información clásica y la cuántica . ${\ Displaystyle \ otimes}$${\ Displaystyle ((a, b), c)}$${\ Displaystyle (a, (b, c))}$${\ displaystyle ()}$

En la teoría de categorías , las categorías monoidales pueden usarse para definir el concepto de un objeto monoide y una acción asociada sobre los objetos de la categoría. También se utilizan en la definición de una categoría enriquecida .

Las categorías monoidales tienen numerosas aplicaciones fuera de la teoría de categorías propiamente dicha. Se utilizan para definir modelos para el fragmento multiplicativo de lógica lineal intuicionista . También forman la base matemática del orden topológico en la física de la materia condensada . Categorías monoidales trenzados tienen aplicaciones en la información cuántica , la teoría cuántica de campos , y la teoría de cuerdas .

Definicion formal

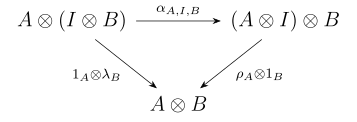
Una categoría monoidal es una categoría equipada con una estructura monoidal. Una estructura monoidal consta de lo siguiente: ${\ Displaystyle \ mathbf {C}}$

• un bifunctor llamado producto tensorial o producto monoidal ,${\ Displaystyle \ otimes \ colon \ mathbf {C} \ times \ mathbf {C} \ to \ mathbf {C}}$
• un objeto llamado objeto unitario u objeto de identidad ,${\ Displaystyle I}$
• tres isomorfismos naturales sujetos a ciertas condiciones de coherencia que expresan el hecho de que la operación tensorial
  • es asociativa: hay un natural (en cada uno de tres argumentos , , ) isomorfismo , llamado asociador , con componentes ,${\ Displaystyle A}$${\ Displaystyle B}$${\ Displaystyle C}$${\ Displaystyle \ alpha}$${\ Displaystyle \ alpha _ {A, B, C} \ colon A \ otimes (B \ otimes C) \ cong (A \ otimes B) \ otimes C}$
  • tiene como identidad izquierda y derecha: hay dos isomorfismos naturales y , respectivamente, denominados unitor izquierdo y derecho , con componentes y .${\ Displaystyle I}$${\ Displaystyle \ lambda}$${\ Displaystyle \ rho}$${\ Displaystyle \ lambda _ {A} \ colon I \ otimes A \ cong A}$${\ Displaystyle \ rho _ {A} \ colon A \ otimes I \ cong A}$

Tenga en cuenta que una buena forma de recordar cómo y actuar es mediante aliteración; Lambda , , anula la identidad de la izquierda , mientras que Rho , , anula la identidad de la derecha . ${\ Displaystyle \ lambda}$${\ Displaystyle \ rho}$${\ Displaystyle \ lambda}$${\ Displaystyle \ rho}$

Las condiciones de coherencia para estas transformaciones naturales son:

• para todos , , y en , el Pentágono diagrama${\ Displaystyle A}$${\ Displaystyle B}$${\ Displaystyle C}$${\ Displaystyle D}$${\ Displaystyle \ mathbf {C}}$

conmuta ;

• para todos y adentro , el diagrama de triángulo${\ Displaystyle A}$${\ Displaystyle B}$${\ Displaystyle \ mathbf {C}}$

conmuta.

Una categoría monoidal estricta es aquella para la que los isomorfismos naturales α , λ y ρ son identidades. Cada categoría monoidal es monoidalmente equivalente a una categoría monoidal estricta.

Ejemplos de

• Cualquier categoría con productos finitos puede considerarse monoidal con el producto como producto monoidal y el objeto terminal como unidad. Esta categoría a veces se denomina categoría monoidal cartesiana . Por ejemplo:
  • Conjunto , la categoría de conjuntos con el producto cartesiano, cualquier conjunto de un elemento particular que actúa como unidad.
  • Cat , la categoría de categorías pequeñas con la categoría de producto , donde la categoría con un objeto y solo su mapa de identidad es la unidad.
• Doblemente, cualquier categoría con coproductos finitos es monoidal con el coproducto como producto monoidal y el objeto inicial como unidad. Tal categoría monoidal se llama monoidal cocartesiana.
• R -Mod , la categoría de módulos sobre un anillo conmutativo R , es una categoría monoidal con el producto tensorial de los módulos ⊗ _R sirviendo como producto monoidal y el anillo R (pensado como un módulo sobre sí mismo) sirviendo como unidad. Como casos especiales se tiene:
  • K -Vect , la categoría de espacios vectoriales sobre un campo K , con el espacio vectorial unidimensional K que sirve como unidad.
  • Ab , la categoría de grupos abelianos , con el grupo de enteros Z como unidad.
• Para cualquier anillo conmutativo R , la categoría de R -álgebras es monoidal con el producto tensorial de álgebras como producto y R como unidad.
• La categoría de espacios puntiagudos (restringidos a espacios generados de forma compacta, por ejemplo) es monoidal con el producto smash como producto y la esfera 0 puntiaguda (un espacio discreto de dos puntos) como unidad.
• La categoría de todos los endofunctores en una categoría C es una categoría monoidal estricta con la composición de los functores como producto y el funtor de identidad como unidad.
• Al igual que para cualquier categoría E , la subcategoría completa abarcada por cualquier objeto dado es un monoide, es el caso de que para cualquier categoría E 2 y cualquier objeto C en Ob ( E ), la subcategoría 2 completa de E abarcada por { C } es una categoría monoidal. En el caso E = Cat , obtenemos el ejemplo de endofunctores anterior.
• Las semirreticulaciones de encuentro delimitado por encima son categorías monoidales simétricas estrictas : el producto se cumple y la identidad es el elemento superior.
• Cualquier monoide ordinario es una pequeña categoría monoidal con conjunto de objetos , solo identidades para morfismos , como producto tensorial y como su objeto de identidad. A la inversa, el conjunto de clases de isomorfismo (si tal cosa tiene sentido) de una categoría monoidal es un monoide con el producto tensorial.${\ Displaystyle (M, \ cdot, 1)}$${\ Displaystyle M}$${\ Displaystyle \ cdot}$${\ Displaystyle 1}$

Pedidos anticipados monoidales

Los pedidos anticipados monoidales, también conocidos como "monoides pedidos anticipados", son casos especiales de categorías monoidales. Este tipo de estructura surge en la teoría de los sistemas de reescritura de cadenas , pero también abunda en las matemáticas puras. Por ejemplo, el conjunto de números naturales tiene una estructura monoide (usando + y 0) y una estructura de preorden (usando ≤), que juntas forman un preorden monoidal, básicamente porque e implica . Presentamos ahora el caso general. ${\ Displaystyle \ mathbb {N}}$${\ Displaystyle m \ leq n}$${\ Displaystyle m '\ leq n'}$${\ Displaystyle m + m '\ leq n + n'}$

Es bien sabido que un orden previo se puede considerar como una categoría C , de manera que por cada dos objetos , existe a lo sumo un morfismo en C . Si sucede que hay un morfismo de c a c ' , podríamos escribir , pero en la sección actual nos resulta más conveniente expresar este hecho en forma de flecha . Debido a que existe a lo sumo uno de esos morfismos, nunca tenemos que darle un nombre, como . Los reflexividad y transitividad propiedades de un pedido se contabilizan respectivamente por el morfismo identidad y la fórmula de composición en C . Escribimos si y sólo si y , es decir, si son isomorfos en C . Tenga en cuenta que en un orden parcial , dos objetos isomorfos cualesquiera son de hecho iguales. ${\ Displaystyle c, c '\ in \ mathrm {Ob} (\ mathbf {C})}$${\ Displaystyle c \ to c '}$${\ Displaystyle c \ leq c '}$${\ Displaystyle c \ to c '}$${\ Displaystyle f \ dos puntos c \ a c '}$${\ Displaystyle c \ cong c '}$${\ Displaystyle c \ leq c '}$${\ Displaystyle c '\ leq c}$

En el futuro, supongamos que queremos añadir una estructura monoidal a la orden previo C . Hacerlo significa que debemos elegir

• un objeto , llamado unidad monoidal , y${\ Displaystyle I \ in \ mathbf {C}}$
• un funtor , que denotaremos simplemente por el punto " ", llamado multiplicación monoidal .${\ Displaystyle \ mathbf {C} \ times \ mathbf {C} \ to \ mathbf {C}}$${\ Displaystyle \; \ cdot \;}$

Por tanto, para dos objetos cualesquiera tenemos un objeto . Debemos elegir y ser asociativos y unitales, hasta el isomorfismo. Esto significa que debemos tener: ${\ Displaystyle c_ {1}, c_ {2}}$${\ Displaystyle c_ {1} \ cdot c_ {2}}$${\ Displaystyle I}$${\ Displaystyle \ cdot}$

${\ Displaystyle (c_ {1} \ cdot c_ {2}) \ cdot c_ {3} \ cong c_ {1} \ cdot (c_ {2} \ cdot c_ {3})}$y .${\ Displaystyle I \ cdot c \ cong c \ cong c \ cdot I}$

Además, el hecho de que · se requiera que sea un funtor significa, en el presente caso, donde C es un preorden, nada más que lo siguiente:

si y luego .${\ Displaystyle c_ {1} \ to c_ {1} '}$${\ Displaystyle c_ {2} \ to c_ {2} '}$${\ Displaystyle (c_ {1} \ cdot c_ {2}) \ to (c_ {1} '\ cdot c_ {2}')}$

Las condiciones de coherencia adicionales para las categorías monoidales son vacías en este caso porque cada diagrama conmuta en un preorden.

Tenga en cuenta que si C es un orden parcial, la descripción anterior se simplifica aún más, porque los isomorfismos de asociatividad y unitalidad se convierten en igualdades. Otra simplificación ocurre si asumimos que el conjunto de objetos es el monoide libre en un grupo electrógeno . En este caso podríamos escribir , donde * denota la estrella de Kleene y la unidad monoidal I representa la cuerda vacía. Si partimos de un conjunto R de generar morfismos (hechos sobre ≤), recuperamos la noción habitual de sistema semi-Thue , donde R se denomina "regla de reescritura". ${\ Displaystyle \ Sigma}$${\ Displaystyle \ mathrm {Ob} (\ mathbf {C}) = \ Sigma ^ {*}}$

Para volver a nuestro ejemplo, sea N la categoría cuyos objetos son los números naturales 0, 1, 2, ..., con un solo morfismo si está en el orden habitual (y sin morfismos de i a j en caso contrario), y un monoidal. estructura con la unidad de monoidal dada por 0 y la multiplicación monoidal dado por la adición de costumbre, . Entonces N es un preorden monoidal; de hecho es el generado libremente por un solo objeto 1, y un solo morfismo 0 ≤ 1, donde nuevamente 0 es la unidad monoidal. ${\ Displaystyle i \ a j}$${\ Displaystyle i \ leq j}$${\ Displaystyle i \ cdot j: = i + j}$

Propiedades y nociones asociadas

De las tres que definen las condiciones de coherencia que una gran clase de diagramas (es decir, diagramas cuyos morfismos son construidos usando , , , identidades y producto tensorial) conmutan: esto es Mac Lane " coherencia teorema ". A veces se dice incorrectamente que todos estos diagramas se desplazan al trabajo. ${\ Displaystyle \ alpha}$${\ Displaystyle \ lambda}$${\ Displaystyle \ rho}$

Existe una noción general de objeto monoide en una categoría monoidal, que generaliza la noción ordinaria de monoide a partir del álgebra abstracta . Los monoides ordinarios son precisamente los objetos monoides en el conjunto de categoría monoidal cartesiano . Además, cualquier categoría monoidal estricta (pequeña) puede verse como un objeto monoide en la categoría de categorías Cat (equipado con la estructura monoidal inducida por el producto cartesiano).

Los functores monoidales son los functores entre categorías monoidales que preservan el producto tensorial y las transformaciones naturales monoidales son las transformaciones naturales, entre esos functores, que son "compatibles" con el producto tensorial.

Cada categoría monoidal puede verse como la categoría B (∗, ∗) de una bicategoría B con un solo objeto, denotado ∗.

El concepto de una categoría C enriquecido en una categoría monoidal M sustituye a la noción de un conjunto de morfismos entre pares de objetos en C con la noción de un M -objeto de morfismos entre cada dos objetos en C .

Categoría monoidal estricta libre

Para cada categoría C , la categoría monoidal estricta libre Σ ( C ) se puede construir de la siguiente manera:

• sus objetos son listas (sucesiones finitas) A ₁ , ..., A _n de objetos de C ;
• hay flechas entre dos objetos A ₁ , ..., A _m y B ₁ , ..., B _n sólo si m = n , y luego las flechas son listas (secuencias finitas) de flechas f ₁ : A ₁ → B ₁ , ..., f _n : A _n → B _n de C ;
• el producto tensorial de dos objetos A ₁ , ..., A _n y B ₁ , ..., B _m es la concatenación A ₁ , ..., A _n , B ₁ , ..., B _m de los dos listas y, de manera similar, el producto tensorial de dos morfismos viene dado por la concatenación de listas. El objeto de identidad es la lista vacía.

Esta operación Σ mapeo de categoría C a Σ ( C ) se puede extender a una estricta 2 mónada en Cat .

Especializaciones

• Si, en una categoría monoidal, y son naturalmente isomorfos de manera compatible con las condiciones de coherencia, hablamos de una categoría monoidal trenzada . Si, además, este isomorfismo natural es su propio inverso, tenemos una categoría monoidal simétrica .${\ Displaystyle A \ otimes B}$${\ Displaystyle B \ otimes A}$
• Una categoría monoidal cerrada es una categoría monoidal en la que el funtor tiene un adjunto derecho , que se denomina "functor Hom interno" . Los ejemplos incluyen categorías cerradas cartesianas como Set , la categoría de conjuntos, y categorías cerradas compactas como FdVect , la categoría de espacios vectoriales de dimensión finita.${\ Displaystyle X \ mapsto X \ otimes A}$${\ Displaystyle X \ mapsto \ mathrm {Hom} _ {\ mathbf {C}} (A, X)}$
• Categorías Autónomas (o compacto CERRADO o categorías rígidas ) son categorías monoidales en las que existen duales con propiedades agradables; abstraen la idea de FdVect .
• Daga de categorías monoidales simétricas , equipada con un funtor de daga extra, abstrayendo la idea de FdHilb , espacios de Hilbert de dimensión finita. Estos incluyen las categorías compactas de daga .
• Las categorías tannakianas son categorías monoidales enriquecidas sobre un campo, que son muy similares a las categorías de representación de grupos algebraicos lineales .

Ver también

• Esqueleto (teoría de categorías)
• Categoría esférica
• Acción de categoría monoidal

Referencias

• Joyal, André ; Calle, Ross (1993). "Categorías de tensor trenzado". Avances en matemáticas 102 , 20–78.
• Joyal, André ; Calle, Ross (1988). " Diagramas planares y álgebra tensorial ".
• Kelly, G. Max (1964). "Sobre las condiciones de MacLane para la coherencia de asociatividades naturales, conmutatividades, etc." Journal of Algebra 1 , 397–402
• Kelly, G. Max (1982). Conceptos básicos de la teoría de categorías enriquecida (PDF) . London Mathematical Society Lecture Note Series No. 64. Cambridge University Press.
• Mac Lane, Saunders (1963). "Asociatividad natural y conmutatividad". Rice University Studies 49 , 28–46.
• Mac Lane, Saunders (1998), Categorías para el matemático que trabaja (2ª ed.). Nueva York: Springer-Verlag.
• Categoría monoidal en nLab

enlaces externos

• Medios relacionados con la categoría Monoidal en Wikimedia Commons