Función de ventana - Window function
En el procesamiento de señales y estadísticas , una función de ventana (también conocida como función de apodización o función de disminución ) es una función matemática que tiene un valor cero fuera de algún intervalo elegido , normalmente simétrica alrededor de la mitad del intervalo, generalmente cerca de un máximo en el intervalo. en el medio y, por lo general, se aleja del centro. Matemáticamente, cuando otra función o forma de onda / secuencia de datos se "multiplica" por una función de ventana, el producto también tiene un valor cero fuera del intervalo: todo lo que queda es la parte donde se superponen, la "vista a través de la ventana". De manera equivalente, y en la práctica real, el segmento de datos dentro de la ventana se aísla primero y luego solo esos datos se multiplican por los valores de la función de ventana. Por lo tanto, la reducción gradual , no la segmentación, es el objetivo principal de las funciones de ventana.
Las razones para examinar segmentos de una función más larga incluyen la detección de eventos transitorios y el promedio temporal de los espectros de frecuencia. La duración de los segmentos se determina en cada aplicación por requisitos como resolución de tiempo y frecuencia. Pero ese método también cambia el contenido de frecuencia de la señal mediante un efecto llamado fuga espectral . Las funciones de ventana nos permiten distribuir la fuga espectralmente de diferentes formas, según las necesidades de la aplicación en particular. Hay muchas opciones detalladas en este artículo, pero muchas de las diferencias son tan sutiles que resultan insignificantes en la práctica.
En aplicaciones típicas, las funciones de ventana utilizadas son curvas no negativas, suaves y en forma de campana. También se pueden utilizar funciones de rectángulo, triángulo y otras. Una definición más general de las funciones de ventana no requiere que sean idénticamente cero fuera de un intervalo, siempre que el producto de la ventana multiplicado por su argumento sea integrable al cuadrado y, más específicamente, que la función vaya lo suficientemente rápido hacia cero.
Aplicaciones
Las funciones de ventana se utilizan en el análisis / modificación / resíntesis espectral , el diseño de filtros de respuesta a impulsos finitos , así como la formación de haces y el diseño de antenas .
Análisis espectral
La transformada de Fourier de la función cos ( ωt ) es cero, excepto en la frecuencia ± ω . Sin embargo, muchas otras funciones y formas de onda no tienen transformaciones de forma cerrada convenientes. Alternativamente, uno podría estar interesado en su contenido espectral solo durante un cierto período de tiempo.
En cualquier caso, la transformada de Fourier (o una transformada similar) se puede aplicar en uno o más intervalos finitos de la forma de onda. En general, la transformación se aplica al producto de la forma de onda y una función de ventana. Cualquier ventana (incluida la rectangular) afecta la estimación espectral calculada por este método.

Elección de la función de ventana
La creación de ventanas de una forma de onda simple como cos ( ωt ) hace que su transformada de Fourier desarrolle valores distintos de cero (comúnmente llamado fuga espectral ) en frecuencias distintas de ω . La fuga tiende a ser peor (más alta) cerca de ω y menos en las frecuencias más alejadas de ω .
Si la forma de onda bajo análisis comprende dos sinusoides de diferentes frecuencias, la fuga puede interferir con nuestra capacidad para distinguirlas espectralmente. Los posibles tipos de interferencia a menudo se dividen en dos clases opuestas de la siguiente manera: si las frecuencias de los componentes son diferentes y un componente es más débil, entonces la fuga del componente más fuerte puede oscurecer la presencia del más débil. Pero si las frecuencias son demasiado similares, las fugas pueden hacerlas irresolubles incluso cuando las sinusoides tienen la misma fuerza. Las ventanas que son efectivas contra el primer tipo de interferencia, es decir, cuando los componentes tienen frecuencias y amplitudes diferentes, se denominan rango dinámico alto . Por el contrario, las ventanas que pueden distinguir componentes con frecuencias y amplitudes similares se denominan de alta resolución .
La ventana rectangular es un ejemplo de una ventana que es de alta resolución pero bajo rango dinámico , lo que significa que es buena para distinguir componentes de amplitud similar incluso cuando las frecuencias también están cerca, pero es pobre para distinguir componentes de diferente amplitud incluso cuando las frecuencias están lejos. lejos. Las ventanas de alta resolución y bajo rango dinámico, como la ventana rectangular, también tienen la propiedad de alta sensibilidad , que es la capacidad de revelar sinusoides relativamente débiles en presencia de ruido aleatorio aditivo. Esto se debe a que el ruido produce una respuesta más fuerte con ventanas de alto rango dinámico que con ventanas de alta resolución.
En el otro extremo de la gama de tipos de ventanas se encuentran las ventanas con alto rango dinámico pero baja resolución y sensibilidad. Las ventanas de alto rango dinámico se justifican con mayor frecuencia en aplicaciones de banda ancha , donde se espera que el espectro que se analiza contenga muchos componentes diferentes de diversas amplitudes.
Entre los extremos hay ventanas moderadas, como Hamming y Hann . Se utilizan comúnmente en aplicaciones de banda estrecha , como el espectro de un canal telefónico.
En resumen, el análisis espectral implica un compromiso entre resolver componentes de fuerza comparables con frecuencias similares ( alta resolución / sensibilidad ) y resolver componentes de fuerza dispares con frecuencias diferentes ( rango dinámico alto ). Esa compensación se produce cuando se elige la función de ventana.
Señales de tiempo discreto
Cuando la forma de onda de entrada se muestrea en el tiempo, en lugar de ser continua, el análisis generalmente se realiza aplicando una función de ventana y luego una transformada discreta de Fourier (DFT). Pero la DFT proporciona solo una muestra escasa del espectro real de la transformada de Fourier de tiempo discreto (DTFT). La figura 2, fila 3, muestra una DTFT para una sinusoide de ventana rectangular. La frecuencia real de la sinusoide se indica como "13" en el eje horizontal. Todo lo demás es una fuga, exagerada por el uso de una presentación logarítmica. La unidad de frecuencia es "bins DFT"; es decir, los valores enteros en el eje de frecuencia corresponden a las frecuencias muestreadas por la DFT. Entonces, la figura representa un caso en el que la frecuencia real de la sinusoide coincide con una muestra de DFT, y esa muestra mide con precisión el valor máximo del espectro. En la fila 4, pierde el valor máximo por ½ bin, y el error de medición resultante se conoce como pérdida festoneada (inspirada en la forma del pico). Para una frecuencia conocida, como una nota musical o una señal de prueba sinusoidal, la coincidencia de la frecuencia con un contenedor DFT se puede preestablecer mediante elecciones de una frecuencia de muestreo y una longitud de ventana que da como resultado un número entero de ciclos dentro de la ventana.
Ancho de banda de ruido
Los conceptos de resolución y rango dinámico tienden a ser algo subjetivos, dependiendo de lo que el usuario esté tratando de hacer. Pero también tienden a estar altamente correlacionados con la fuga total, que es cuantificable. Por lo general, se expresa como un ancho de banda equivalente, B. Se puede pensar que redistribuye la DTFT en una forma rectangular con una altura igual al máximo espectral y al ancho B. Cuanto mayor es la fuga, mayor es el ancho de banda. A veces se denomina ancho de banda de ruido equivalente o ancho de banda de ruido equivalente , porque es proporcional a la potencia promedio que será registrada por cada contenedor DFT cuando la señal de entrada contiene un componente de ruido aleatorio (o es simplemente ruido aleatorio). Un gráfico del espectro de potencia , promediado a lo largo del tiempo, generalmente revela un piso de ruido plano , causado por este efecto. La altura del piso de ruido es proporcional a B. Por lo tanto, dos funciones de ventana diferentes pueden producir diferentes pisos de ruido.
Procesamiento de pérdidas y ganancias
En el procesamiento de señales , las operaciones se eligen para mejorar algún aspecto de la calidad de una señal explotando las diferencias entre la señal y las influencias corruptoras. Cuando la señal es una sinusoide corrompida por ruido aleatorio aditivo, el análisis espectral distribuye los componentes de la señal y el ruido de manera diferente, lo que a menudo facilita la detección de la presencia de la señal o la medición de ciertas características, como la amplitud y la frecuencia. Efectivamente, la relación señal / ruido (SNR) se mejora al distribuir el ruido de manera uniforme, mientras se concentra la mayor parte de la energía de la sinusoide alrededor de una frecuencia. La ganancia de procesamiento es un término que se usa a menudo para describir una mejora de SNR. La ganancia de procesamiento del análisis espectral depende de la función de la ventana, tanto de su ancho de banda de ruido (B) como de su potencial pérdida de festón. Estos efectos se compensan parcialmente, porque las ventanas con menos festoneado naturalmente tienen la mayor cantidad de fugas.
La Figura 3 muestra los efectos de tres funciones de ventana diferentes en el mismo conjunto de datos, que comprende dos sinusoides de igual intensidad en ruido aditivo. Las frecuencias de las sinusoides se eligen de modo que una no encuentre festoneado y la otra encuentre el máximo festoneado. Ambos sinusoides sufren menos pérdida de SNR debajo de la ventana de Hann que debajo de la ventana de Blackman - Harris . En general (como se mencionó anteriormente), esto disuade el uso de ventanas de alto rango dinámico en aplicaciones de bajo rango dinámico.
Simetría
Las fórmulas proporcionadas en este artículo producen secuencias discretas, como si se hubiera "muestreado" una función de ventana continua. (Vea un ejemplo en la ventana de Kaiser ). Las secuencias de ventanas para el análisis espectral son simétricas o una muestra menos que simétricas (llamadas periódicas , DFT-par o DFT-simétricas ). Por ejemplo, la función MATLAB genera una secuencia simétrica verdadera, con su máximo en un solo punto central hann(9,'symmetric'). Eliminar la última muestra produce una secuencia idéntica a hann(8,'periodic'). De manera similar, la secuencia hann(8,'symmetric')tiene dos puntos centrales iguales.
Algunas funciones tienen uno o dos puntos finales con valor cero, que son innecesarios en la mayoría de las aplicaciones. Eliminar un punto final de valor cero no tiene ningún efecto en su DTFT (fuga espectral). Pero la función diseñada para muestras N + 1 o N + 2, en previsión de eliminar uno o ambos puntos finales, normalmente tiene un lóbulo principal ligeramente más estrecho, lóbulos laterales ligeramente más altos y un ancho de banda de ruido ligeramente menor.
Simetría DFT
El predecesor de la DFT es la transformada finita de Fourier , y las funciones de ventana eran "siempre un número impar de puntos y exhibían una simetría par sobre el origen". En ese caso, la DTFT tiene un valor completamente real. Cuando la misma secuencia se cambia a una ventana de datos DFT , la DTFT se vuelve de valor complejo, excepto en frecuencias espaciadas a intervalos regulares de Por lo tanto, cuando se muestrea mediante una DFT de longitud (ver suma periódica ), las muestras (llamadas coeficientes DFT ) son todavía valioso. Eso también es cierto para una DFT de longitud de la secuencia simétrica de DFT truncada : el truncamiento afecta la DTFT (fuga espectral), pero normalmente en una cantidad insignificante (a menos que sea pequeña, por ejemplo, ≤ 20 ).
Cuando las ventanas se aplican multiplicativamente a datos reales, la secuencia generalmente carece de simetría y la DFT generalmente no tiene valores reales. A pesar de esta advertencia, muchos autores asumen reflexivamente ventanas simétricas DFT. Por lo tanto, vale la pena señalar que no existe una ventaja de rendimiento cuando se aplica a los datos del dominio del tiempo, que es la aplicación habitual. La ventaja de los coeficientes DFT de valor real se realiza en ciertas aplicaciones esotéricas donde la creación de ventanas se logra mediante la convolución entre los coeficientes DFT y una DFT sin ventana de los datos. En esas aplicaciones, se prefieren las ventanas simétricas DFT (longitud par o impar) de la familia de suma de coseno , porque la mayoría de sus coeficientes DFT tienen valor cero, lo que hace que la convolución sea muy eficiente.
- Notas
Diseño de filtros
Las ventanas se utilizan a veces en el diseño de filtros digitales , en particular para convertir una respuesta de impulso "ideal" de duración infinita, como una función sinc , en un diseño de filtro de respuesta de impulso finita (FIR). Eso se llama método de ventana .
Estadísticas y ajuste de curvas
Las funciones de ventana se utilizan a veces en el campo del análisis estadístico para restringir el conjunto de datos que se analizan a un rango cerca de un punto dado, con un factor de ponderación que disminuye el efecto de los puntos más alejados de la parte de la curva que se ajusta. En el campo del análisis bayesiano y el ajuste de curvas , esto a menudo se denomina kernel .
Aplicaciones de ventanas rectangulares
Análisis de transitorios
Cuando se analiza una señal transitoria en el análisis modal , como un impulso, una respuesta de choque, una ráfaga sinusoidal, una ráfaga de chirrido o ráfaga de ruido, donde la distribución de energía frente al tiempo es extremadamente desigual, la ventana rectangular puede ser la más apropiada. Por ejemplo, cuando la mayor parte de la energía se encuentra al comienzo de la grabación, una ventana no rectangular atenúa la mayor parte de la energía, degradando la relación señal / ruido.
Análisis armónico
Uno podría desear medir el contenido armónico de una nota musical de un instrumento en particular o la distorsión armónica de un amplificador a una frecuencia dada. Refiriéndonos nuevamente a la Figura 2 , podemos observar que no hay fugas en un conjunto discreto de frecuencias armónicamente relacionadas muestreadas por el DFT. (Los nulos espectrales son en realidad cruces por cero, que no se pueden mostrar en una escala logarítmica como esta). Esta propiedad es exclusiva de la ventana rectangular y debe configurarse adecuadamente para la frecuencia de la señal, como se describe anteriormente.
Una lista de funciones de la ventana
Convenciones :
- es una función de fase cero (simétrica alrededor ), continua para donde es un número entero positivo (par o impar).
- La secuencia es simétrica , de longitud
- es simétrica DFT , de longitud
- El parámetro B que se muestra en cada gráfico espectral es la métrica de ancho de banda equivalente al ruido de la función, en unidades de contenedores DFT .
El muestreo escaso de un DTFT (como los DFT en la Fig. 2) solo revela la fuga a los contenedores DFT desde una sinusoide cuya frecuencia es también un contenedor DFT entero. Los lóbulos laterales invisibles revelan la fuga que se espera de los sinusoides en otras frecuencias. Por lo tanto, al elegir una función de ventana, generalmente es importante muestrear la DTFT de manera más densa (como lo hacemos a lo largo de esta sección) y elegir una ventana que suprima los lóbulos laterales a un nivel aceptable.
Ventana rectangular
La ventana rectangular (a veces conocida como boxcar o ventana de Dirichlet ) es la ventana más simple, equivalente a reemplazar todos los valores de una secuencia de datos excepto N por ceros, haciendo que parezca que la forma de onda se enciende y apaga repentinamente:
Otras ventanas están diseñadas para moderar estos cambios repentinos, lo que reduce la pérdida de festón y mejora el rango dinámico, como se describió anteriormente ( § Análisis espectral ).
La ventana rectangular es la 1 st orden B ventana -spline así como el 0 º potencia de la ventana de energía de onda sinusoidal .
Ventanas b- spline
Las ventanas de b- spline se pueden obtener como k- pliegues de convoluciones de la ventana rectangular. Incluyen la propia ventana rectangular ( k = 1), la § Ventana triangular ( k = 2) y la § Ventana Parzen ( k = 4). Las definiciones alternativas muestran las funciones de base B- spline normalizadas apropiadas en lugar de convolucionar ventanas de tiempo discreto. A k ésimo -order B función de base -spline es una función polinómica por tramos de grado k -1 que se obtiene por k -fold auto-convolución de la función rectangular .
Ventana triangular
Las ventanas triangulares están dadas por:
donde L puede ser N , N + 1 o N + 2. La primera también se conoce como ventana de Bartlett o ventana de Fejér . Las tres definiciones convergen en N grande .
La ventana triangular es la ventana de línea B de segundo orden . La forma L = N puede verse como la convolución de dos ventanas rectangulares de ancho N / 2. La transformada de Fourier del resultado son los valores al cuadrado de la transformada de la ventana rectangular de medio ancho.
Ventana parzen
Definiendo L ≜ N + 1 , la ventana Parzen, también conocida como la ventana de la Vallée Poussin , es la ventana B -spline de cuarto orden dada por:
Otras ventanas polinomiales
Ventana de Welch
La ventana de Welch consta de una única sección parabólica :
El polinomio cuadrático de definición alcanza un valor de cero en las muestras justo fuera del intervalo de la ventana.
Ventana sinusoidal
La función correspondiente es un coseno sin el desplazamiento de fase π / 2. Entonces, la ventana del seno a veces también se llama ventana del coseno . Como representa medio ciclo de una función sinusoidal, también se conoce de forma variable como ventana de medio seno o ventana de medio coseno .
La autocorrelación de una ventana sinusoidal produce una función conocida como ventana de Bohman.
Ventanas de potencia de seno / coseno
Estas funciones de ventana tienen la forma:
La ventana rectangular ( α = 0 ), la ventana sinusoidal ( α = 1 ) y la ventana de Hann ( α = 2 ) son miembros de esta familia.
Para valores enteros pares de α , estas funciones también se pueden expresar en forma de suma de coseno :
Ventanas de suma de coseno
Esta familia también se conoce como ventanas de coseno generalizadas .
-
( Ecuación 1 )
En la mayoría de los casos, incluidos los ejemplos siguientes, todos los coeficientes a k ≥ 0. Estas ventanas solo tienen 2 K + 1 coeficientes DFT de N puntos distintos de cero .
Ventanas de Hann y Hamming
Las ventanas de suma de coseno habituales para el caso K = 1 tienen la forma:
que se confunde fácilmente (y a menudo) con su versión de fase cero:
El ajuste produce una ventana de Hann:
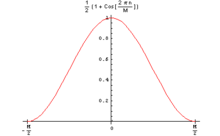
nombrado en honor a Julius von Hann , y a veces denominado Hanning , presumiblemente debido a sus similitudes lingüísticas y formulistas con la ventana de Hamming. También se conoce como coseno elevado , porque la versión de fase cero, es un lóbulo de una función coseno elevada.
Esta función es miembro de las familias de suma de coseno y potencia de seno . A diferencia de la ventana de Hamming , los puntos finales de la ventana de Hann simplemente tocan cero. Los lóbulos laterales resultantes caen a unos 18 dB por octava.
El ajuste a aproximadamente 0,54, o más precisamente a 25/46, produce la ventana Hamming, propuesta por Richard W. Hamming . Esa elección coloca un cruce por cero en la frecuencia 5 π / ( N - 1), que cancela el primer lóbulo lateral de la ventana de Hann, dándole una altura de aproximadamente una quinta parte de la de la ventana de Hann. La ventana de Hamming a menudo se denomina señal de Hamming cuando se usa para dar forma al pulso .
La aproximación de los coeficientes a dos lugares decimales reduce sustancialmente el nivel de los lóbulos laterales, a una condición de casi equiripulación. En el sentido de equiripulación, los valores óptimos para los coeficientes son 0 = 0,53836 y 1 = 0,46164.
Ventana de Blackman
Las ventanas de Blackman se definen como:
Por convención común, el término no calificado de ventana de Blackman se refiere a la "propuesta no muy seria" de Blackman de α = 0.16 ( a 0 = 0.42, a 1 = 0.5, a 2 = 0.08), que se aproxima mucho al Blackman exacto , con un 0 = 7938/18608 ≈ 0.42659, a 1 = 9240/18608 ≈ 0.49656 y a 2 = 1430/18608 ≈ 0.076849. Estos valores exactos colocan ceros en el tercer y cuarto lóbulo lateral, pero dan como resultado una discontinuidad en los bordes y una caída de 6 dB / oct. Los coeficientes truncados no anulan también los lóbulos laterales, pero tienen una caída mejorada de 18 dB / oct.
Ventana Nuttall, primera derivada continua
La forma continua de la ventana Nuttall y su primera derivada son continuas en todas partes, como la función de Hann . Es decir, la función va a 0 en x = ± N / 2, a diferencia de las ventanas Blackman-Nuttall, Blackman-Harris y Hamming. La ventana de Blackman ( α = 0.16 ) también es continua con derivada continua en el borde, pero la "ventana exacta de Blackman" no lo es.
Ventana de Blackman – Nuttall
Ventana de Blackman – Harris
Una generalización de la familia Hamming, producida al agregar más funciones sinc desplazadas, destinada a minimizar los niveles de los lóbulos laterales.
Ventana superior plana
Una ventana superior plana es una ventana con valor parcialmente negativo que tiene una mínima pérdida de festón en el dominio de la frecuencia. Esa propiedad es deseable para la medición de amplitudes de componentes de frecuencia sinusoidal. Los inconvenientes del ancho de banda amplio son una resolución de frecuencia deficiente y un ancho de banda de ruido elevado .
Las ventanas de techo plano se pueden diseñar utilizando métodos de diseño de filtro de paso bajo, o pueden ser de la variedad habitual de suma de coseno :
La variante de Matlab tiene estos coeficientes:
Hay otras variaciones disponibles, como los lóbulos laterales que se deslizan a costa de valores más altos cerca del lóbulo principal.
Ventanas de Rife-Vincent
Las ventanas de Rife-Vincent se escalan habitualmente para el valor promedio unitario, en lugar del valor pico unitario. Los valores de los coeficientes a continuación, aplicados a la Ec. 1 , reflejan esa costumbre.
Clase I, orden 1 ( K = 1): funcionalmente equivalente a la ventana de Hann .
Clase I, orden 2 ( K = 2):
La clase I se define minimizando la amplitud de los lóbulos laterales de alto orden. Se tabulan los coeficientes para pedidos hasta K = 4.
La clase II minimiza el ancho del lóbulo principal para un lóbulo lateral máximo dado.
La clase III es un compromiso para el que el orden K = 2 se asemeja a la ventana de § Blackman .
Ventanas ajustables
Ventana gaussiana
La transformada de Fourier de un gaussiano también es un gaussiano. Dado que el soporte de una función gaussiana se extiende hasta el infinito, debe estar truncado en los extremos de la ventana o en sí misma con otra ventana de extremo cero.
Dado que el logaritmo de un gaussiano produce una parábola , esto se puede utilizar para una interpolación cuadrática casi exacta en la estimación de frecuencia .
La desviación estándar de la función gaussiana es σ · N / 2 períodos de muestreo.
Ventana gaussiana confinada
La ventana gaussiana confinada produce el ancho de frecuencia cuadrático medio más pequeño posible σ ω para un ancho temporal dado ( N + 1) σ t . Estas ventanas optimizan los productos de ancho de banda de tiempo-frecuencia RMS. Se calculan como los vectores propios mínimos de una matriz dependiente de parámetros. La familia de ventanas gaussianas confinadas contiene la ventana sinusoidal § y la ventana gaussiana § en los casos límite de σ t grande y pequeña , respectivamente.
Ventana gaussiana confinada aproximada
Definiendo L ≜ N + 1 , una ventana gaussiana confinada de ancho temporal L × σ t se aproxima bien por:
donde es una función gaussiana:
La desviación estándar de la ventana aproximada es asintóticamente igual (es decir, valores grandes de N ) a L × σ t para σ t <0,14 .
Ventana normal generalizada
Una versión más generalizada de la ventana gaussiana es la ventana normal generalizada. Conservando la notación de la ventana gaussiana anterior, podemos representar esta ventana como
para cualquiera . En , esta es una ventana gaussiana y, a medida que se acerca , se aproxima a una ventana rectangular. La transformada de Fourier de esta ventana no existe en forma cerrada para un general . Sin embargo, demuestra los otros beneficios de ser un ancho de banda suave y ajustable. Al igual que la ventana de § Tukey , esta ventana ofrece naturalmente una "parte superior plana" para controlar la atenuación de amplitud de una serie de tiempo (en la que no tenemos un control con la ventana gaussiana). En esencia, ofrece un buen compromiso (controlable), en términos de fuga espectral, resolución de frecuencia y atenuación de amplitud, entre la ventana gaussiana y la ventana rectangular. Consulte también un estudio sobre la representación de frecuencia de tiempo de esta ventana (o función).
Ventana de tukey
La ventana de Tukey, también conocida como ventana cónica del coseno , se puede considerar como un lóbulo coseno de ancho Nα / 2 (que abarca observaciones Nα / 2 + 1 ) que se convoluciona con una ventana rectangular de ancho N (1 - α / 2 ) .
En α = 0 se vuelve rectangular y en α = 1 se convierte en una ventana de Hann.
Ventana cónica de Planck
La llamada ventana "Planck-taper" es una función de relieve que se ha utilizado ampliamente en la teoría de particiones de unidad en variedades . Es suave (una función) en todas partes, pero es exactamente cero fuera de una región compacta, exactamente uno en un intervalo dentro de esa región, y varía suave y monótonamente entre esos límites. Su uso como función de ventana en el procesamiento de señales se sugirió por primera vez en el contexto de la astronomía de ondas gravitacionales , inspirada en la distribución de Planck . Se define como una función por partes :
La cantidad de disminución se controla mediante el parámetro ε , con valores más pequeños que dan transiciones más nítidas.
Ventana DPSS o Slepian
La ventana DPSS (secuencia esferoidal prolate discreta) o ventana de Slepian maximiza la concentración de energía en el lóbulo principal y se utiliza en el análisis espectral de múltiples cónicos , que promedia el ruido en el espectro y reduce la pérdida de información en los bordes de la ventana.
El lóbulo principal termina en un intervalo de frecuencia dado por el parámetro α .
Las ventanas de Kaiser a continuación se crean mediante una aproximación simple a las ventanas de DPSS:
Ventana de Kaiser
La ventana de Kaiser, o Kaiser-Bessel, es una aproximación simple de la ventana DPSS usando funciones de Bessel , descubierta por James Kaiser .
donde es la función de Bessel modificada de orden cero del primer tipo. El parámetro variable determina la compensación entre el ancho del lóbulo principal y los niveles del lóbulo lateral del patrón de fuga espectral. El ancho del lóbulo principal, entre los nulos, está dado por en unidades de contenedores DFT, y un valor típico de es 3.
Ventana Dolph – Chebyshev
Minimiza la norma de Chebyshev de los lóbulos laterales para un ancho de lóbulo principal dado.
La función de ventana Dolph-Chebyshev de fase cero generalmente se define en términos de su transformada discreta de Fourier de valor real :
T n ( x ) es el n -ésimo polinomio de Chebyshev del primer tipo evaluado en x , que se puede calcular usando
y
es la única solución real positiva a , donde el parámetro α establece la norma de Chebyshev de los lóbulos laterales en −20 α decibeles.
La función de ventana se puede calcular a partir de W 0 ( k ) mediante una transformada de Fourier discreta inversa (DFT):
La versión retrasada de la ventana se puede obtener mediante:
que para valores pares de N debe calcularse de la siguiente manera:
que es una DFT inversa de
Variaciones:
- Debido a la condición de equiripulación, la ventana del dominio del tiempo tiene discontinuidades en los bordes. Una aproximación que los evita, al permitir que los equiripples caigan en los bordes, es una ventana de Taylor .
- También está disponible una alternativa a la definición DFT inversa. [1] .
Ventana ultraesférica
La ventana ultraesférica fue introducida en 1984 por Roy Streit y tiene aplicación en el diseño de conjuntos de antenas, diseño de filtros no recursivos y análisis de espectro.
Al igual que otras ventanas ajustables, la ventana ultraesférica tiene parámetros que se pueden usar para controlar el ancho del lóbulo principal de la transformada de Fourier y la amplitud relativa del lóbulo lateral. Poco común en otras ventanas, tiene un parámetro adicional que se puede usar para establecer la velocidad a la que los lóbulos laterales disminuyen (o aumentan) en amplitud.
La ventana se puede expresar en el dominio del tiempo de la siguiente manera:
donde es el polinomio ultraesférico de grado N, y y controla los patrones de los lóbulos laterales.
Ciertos valores específicos de ceden otras ventanas conocidas: y dan las ventanas Dolph – Chebyshev y Saramäki respectivamente. Consulte aquí la ilustración de las ventanas ultraesféricas con parametrización variada.
Ventana exponencial o de Poisson
La ventana de Poisson, o más genéricamente la ventana exponencial, aumenta exponencialmente hacia el centro de la ventana y disminuye exponencialmente en la segunda mitad. Dado que la función exponencial nunca llega a cero, los valores de la ventana en sus límites son distintos de cero (se puede ver como la multiplicación de una función exponencial por una ventana rectangular). Está definido por
donde τ es la constante de tiempo de la función. La función exponencial decae como e ≃ 2,71828 o aproximadamente 8,69 dB por constante de tiempo. Esto significa que para un decaimiento objetivo de D dB sobre la mitad de la longitud de la ventana, la constante de tiempo τ viene dada por
Ventanas híbridas
Las funciones de ventana también se han construido como combinaciones multiplicativas o aditivas de otras ventanas.
Ventana de Bartlett – Hann
Ventana de Planck-Bessel
Una ventana de § Planck-taper multiplicada por una ventana de Kaiser que se define en términos de una función de Bessel modificada . Esta función de ventana híbrida se introdujo para disminuir el nivel máximo de lóbulos laterales de la ventana de ahusamiento de Planck sin dejar de explotar su buena desintegración asintótica. Tiene dos parámetros ajustables, ε de Planck-taper y α de la ventana de Kaiser, por lo que se puede ajustar para adaptarse a los requisitos de una señal determinada.
Ventana de Hann-Poisson
Una ventana de Hann multiplicada por una ventana de Poisson , que no tiene lóbulos laterales, en el sentido de que (para ) su transformada de Fourier se aleja para siempre del lóbulo principal. Por tanto, se puede utilizar en algoritmos de escalada como el método de Newton . La ventana de Hann-Poisson se define por:
donde α es un parámetro que controla la pendiente de la exponencial.
Otras ventanas
Ventana de polinomio adaptativo generalizado (GAP)
La ventana GAP es una familia de funciones de ventana ajustables que se basan en una expansión de orden polinomial simétrica . Es continuo con derivada continua en todas partes. Con el conjunto apropiado de coeficientes de expansión y orden de expansión, la ventana GAP puede imitar todas las funciones de ventana conocidas, reproduciendo con precisión sus propiedades espectrales.
donde es la desviación estándar de la secuencia.
Además, comenzando con un conjunto de coeficientes de expansión que imita una determinada función de ventana conocida, la ventana GAP se puede optimizar mediante procedimientos de minimización para obtener un nuevo conjunto de coeficientes que mejoran una o más propiedades espectrales, como el ancho del lóbulo principal, el lóbulo lateral atenuación y tasa de caída del lóbulo lateral. Por lo tanto, se puede desarrollar una función de ventana GAP con propiedades espectrales diseñadas según la aplicación específica.
Ventana de Lanczos
- utilizado en el remuestreo de Lanczos
- para la ventana de Lanczos, se define como
- también conocida como ventana sinc , porque :
- es el lóbulo principal de una función sinc normalizada
Comparación de ventanas
Al seleccionar una función de ventana adecuada para una aplicación, este gráfico de comparación puede resultar útil. El eje de frecuencia tiene unidades de "contenedores" FFT cuando la ventana de longitud N se aplica a los datos y se calcula una transformada de longitud N. Por ejemplo, el valor a la frecuencia ½ "bin" (tercera marca de verificación) es la respuesta que se mediría en bins k y k + 1 a una señal sinusoidal en la frecuencia k + ½. Es relativo a la respuesta máxima posible, que ocurre cuando la frecuencia de la señal es un número entero de bins. El valor a la frecuencia ½ se conoce como la pérdida máxima de festón de la ventana, que es una métrica utilizada para comparar ventanas. La ventana rectangular es notablemente peor que las demás en términos de esa métrica.
Otras métricas que se pueden ver son el ancho del lóbulo principal y el nivel máximo de los lóbulos laterales, que determinan respectivamente la capacidad para resolver señales de fuerza comparables y señales de fuerza dispares. La ventana rectangular (por ejemplo) es la mejor opción para los primeros y la peor para los segundos. Lo que no se puede ver en los gráficos es que la ventana rectangular tiene el mejor ancho de banda de ruido, lo que la convierte en un buen candidato para detectar sinusoides de bajo nivel en un entorno de ruido blanco . Las técnicas de interpolación, como el relleno de ceros y el cambio de frecuencia, están disponibles para mitigar su potencial pérdida de festón.
Ventanas superpuestas
Cuando la longitud de un conjunto de datos que se va a transformar es mayor de lo necesario para proporcionar la resolución de frecuencia deseada, una práctica común es subdividirlo en conjuntos más pequeños y mostrarlos individualmente. Para mitigar la "pérdida" en los bordes de la ventana, los conjuntos individuales pueden superponerse en el tiempo. Consulte el método de Welch de análisis espectral de potencia y la transformada de coseno discreta modificada .
Ventanas bidimensionales
Las ventanas bidimensionales se utilizan comúnmente en el procesamiento de imágenes para reducir las altas frecuencias no deseadas en la transformada de Fourier de la imagen. Pueden construirse a partir de ventanas unidimensionales en cualquiera de dos formas. La forma separable es trivial de calcular. La forma radial , que involucra el radio , es isotrópica , independiente de la orientación de los ejes coordenados. Solo la función gaussiana es separable e isotrópica. Las formas separables de todas las demás funciones de ventana tienen esquinas que dependen de la elección de los ejes de coordenadas. La isotropía / anisotropía de una función de ventana bidimensional es compartida por su transformada de Fourier bidimensional. La diferencia entre las formas separables y radiales es similar al resultado de la difracción de las aberturas rectangulares frente a las circulares, que se pueden visualizar en términos del producto de dos funciones sinc frente a una función Airy , respectivamente.
Ver también
- Fuga espectral
- Multicónica
- Apodización
- Método de Welch
- Transformada de Fourier de corta duración
- Método de diseño de ventana
- Filtro Kolmogorov – Zurbenko
Notas
Citas de página
Referencias
Otras lecturas
- Harris, Frederic J. (septiembre de 1976). "Windows, análisis armónico y la transformada discreta de Fourier" (PDF) . apps.dtic.mil . Centro submarino naval, San Diego . Consultado el 8 de abril de 2019 .
- Albrecht, Hans-Helge (2012). Ventanas de suma de coseno de lóbulo lateral mínimo y lóbulo lateral mínimo a medida. Versión 1.0 . ISBN 978-3-86918-281-0). editor: Physikalisch-Technische Bundesanstalt. Physikalisch-Technische Bundesanstalt. doi : 10.7795 / 110.20121022aa . ISBN 978-3-86918-281-0.
- Bergen, SWA; Antoniou, A. (2005). "Diseño de filtros digitales no recursivos mediante la función de ventana ultraesférica" . Revista EURASIP sobre procesamiento de señales aplicadas . 2005 (12): 1910–1922. Código bibliográfico : 2005EJASP2005 ... 44B . doi : 10.1155 / ASP.2005.1910 .
- Prabhu, KMM (2014). Funciones de ventana y sus aplicaciones en el procesamiento de señales . Boca Raton, FL: CRC Press. ISBN 978-1-4665-1583-3.
- Patente estadounidense 7065150 , Park, Young-Seo, "Sistema y método para generar una modulación de multiplexación por división de frecuencia ortogonal de coseno elevado de raíz (RRC OFDM)", publicada en 2003, publicada en 2006
enlaces externos
-
 Medios relacionados con la función de ventana en Wikimedia Commons
Medios relacionados con la función de ventana en Wikimedia Commons - Ayuda de LabView, características de los filtros de suavizado, http://zone.ni.com/reference/en-XX/help/371361B-01/lvanlsconcepts/char_smoothing_windows/
- Creación y propiedades de funciones de ventana de suma de coseno, http://electronicsart.weebly.com/fftwindows.html
- FFT interactivo en línea, Windows, resolución y simulación de fugas | RITEC | Biblioteca y herramientas




![{\ Displaystyle [0 \ leq n \ leq N],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26cc1478a6bb711340dd37b5398448eb1b8d9ef6)


![{\ Displaystyle [0 \ leq n \ leq N-1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb6f361f87ffe5498e6b67eeb9d61976220f988)


![{\ Displaystyle x \ in [-N / 2, N / 2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0377d29e5715ebdd13819c1cc07c4638a0156afd)
![{\ Displaystyle \ {w [n] = w_ {0} (nN / 2), \ quad 0 \ leq n \ leq N \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f28eb10c2426fe0deb507ce933eb6b5df2c020e)

![{\ Displaystyle \ {w [n], \ quad 0 \ leq n \ leq N-1 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f506d61ded38a4f9d8ecd59004fbf34e793d81f3)


![{\ Displaystyle w [n] = 1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f071fdd6a0a02d6d9dc3c1325d88a6dda6a92781)
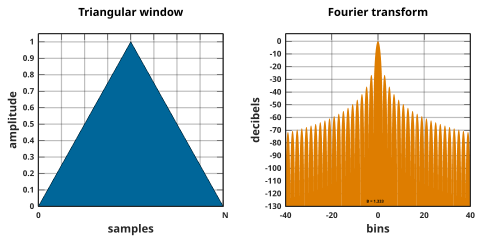
![{\ Displaystyle w [n] = 1- \ left | {\ frac {n - {\ frac {N} {2}}} {\ frac {L} {2}}} \ right |, \ quad 0 \ leq n \ leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884ef77423e593a74ebf40ec3eaa0c8f00ca5102)


![{\ Displaystyle w [n] = \ w_ {0} \ left (n - {\ tfrac {N} {2}} \ right), \ 0 \ leq n \ leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfa5797bd28cc542de9f224e4b9c7c0c37bff91a)

![{\ Displaystyle w [n] = 1- \ left ({\ frac {n - {\ frac {N} {2}}} {\ frac {N} {2}}} \ right) ^ {2}, \ quad 0 \ leq n \ leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3a944c6a5c2051217a53dd60a9693dd76c98a9)

![{\ Displaystyle w [n] = \ sin \ left ({\ frac {\ pi n} {N}} \ right) = \ cos \ left ({\ frac {\ pi n} {N}} - {\ frac {\ pi} {2}} \ right), \ quad 0 \ leq n \ leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2af9f7febc105f1184bd114a1484bf16cf7325)

![{\ Displaystyle w [n] = \ sin ^ {\ alpha} \ left ({\ frac {\ pi n} {N}} \ right) = \ cos ^ {\ alpha} \ left ({\ frac {\ pi n} {N}} - {\ frac {\ pi} {2}} \ right), \ quad 0 \ leq n \ leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b81af4c85e4b5e6909b3dfb7fef170a42a02f7e)
![{\ Displaystyle w [n] = a_ {0} -a_ {1} \ cos \ left ({\ frac {2 \ pi n} {N}} \ right) + a_ {2} \ cos \ left ({\ frac {4 \ pi n} {N}} \ right) -a_ {3} \ cos \ left ({\ frac {6 \ pi n} {N}} \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55aa618bd5010d83e5df4ae06fbb3abd509f12fd)

![{\ Displaystyle w [n] = \ sum _ {k = 0} ^ {K} (- 1) ^ {k} a_ {k} \; \ cos \ left ({\ frac {2 \ pi kn} {N }} \ derecha), \ quad 0 \ leq n \ leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e597f0587d0c29feaf791fef475cf419be2987c9)


![{\ Displaystyle w [n] = a_ {0} - \ underbrace {(1-a_ {0})} _ {a_ {1}} \ cdot \ cos \ left ({\ tfrac {2 \ pi n} {N }} \ derecha), \ quad 0 \ leq n \ leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72b8f8c3192b06191db2bb7ad9247eeba6a6cb70)
![{\ Displaystyle {\ begin {alineado} w_ {0} (n) \ & = w \ left [n + {\ tfrac {N} {2}} \ right] \\ & = a_ {0} + a_ {1} \ cdot \ cos \ left ({\ tfrac {2 \ pi n} {N}} \ right), \ quad - {\ tfrac {N} {2}} \ leq n \ leq {\ tfrac {N} {2 }}. \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a04d79e8c4de591b5badfd2864ebe7522c17b1ad)

![{\ Displaystyle w [n] = 0.5 \; \ left [1- \ cos \ left ({\ frac {2 \ pi n} {N}} \ right) \ right] = \ sin ^ {2} \ left ( {\ frac {\ pi n} {N}} \ right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd8d3e844a1443d7bedd57240588cf19fcd28af1)


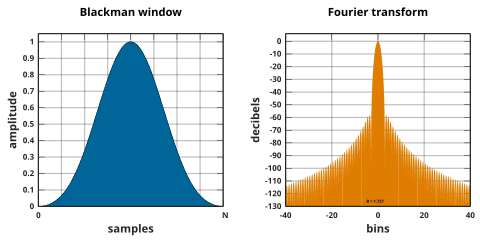
![{\ Displaystyle w [n] = a_ {0} -a_ {1} \ cos \ left ({\ frac {2 \ pi n} {N}} \ right) + a_ {2} \ cos \ left ({\ frac {4 \ pi n} {N}} \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1a6c47fc77da0b81229c3234068706a6ca8e6a)








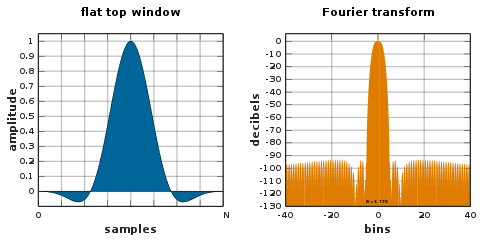
![{\ Displaystyle {\ begin {alineado} w [n] = a_ {0} & {} - a_ {1} \ cos \ left ({\ frac {2 \ pi n} {N}} \ right) + a_ { 2} \ cos \ left ({\ frac {4 \ pi n} {N}} \ right) \\ & {} - a_ {3} \ cos \ left ({\ frac {6 \ pi n} {N} } \ right) + a_ {4} \ cos \ left ({\ frac {8 \ pi n} {N}} \ right). \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e117d087bf8d6345fb6ea8ffc7b5aa7f6faae4a)



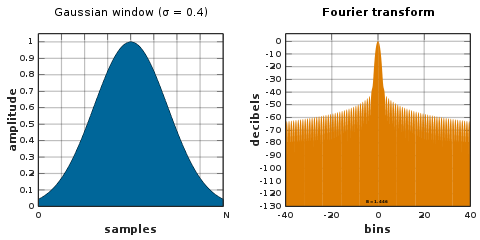
![{\ Displaystyle w [n] = \ exp \ left (- {\ frac {1} {2}} \ left ({\ frac {nN / 2} {\ sigma N / 2}} \ right) ^ {2} \ right), \ quad 0 \ leq n \ leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e201c829f6aabf4339fc0a1929367d5613dfe290)

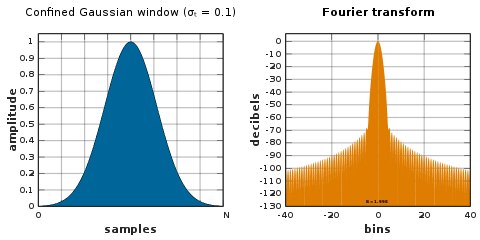

![{\ Displaystyle w [n] = G (n) - {\ frac {G (- {\ tfrac {1} {2}}) [G (n + L) + G (nL)]} {G (- { \ tfrac {1} {2}} + L) + G (- {\ tfrac {1} {2}} - L)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3094fa9469d1e65bfdb6a4e31cdafd037a8822ec)


![{\ Displaystyle w [n, p] = \ exp \ left (- \ left ({\ frac {nN / 2} {\ sigma N / 2}} \ right) ^ {p} \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/704a7de7c2a67fc8a24a140a151491bd7362698c)




![{\ Displaystyle \ left. {\ begin {array} {lll} w [n] = {\ frac {1} {2}} \ left [1- \ cos \ left ({\ frac {2 \ pi n} { \ alpha N}} \ right) \ right], \ quad & 0 \ leq n <{\ frac {\ alpha N} {2}} \\ w [n] = 1, \ quad & {\ frac {\ alpha N } {2}} \ leq n \ leq {\ frac {N} {2}} \\ w [Nn] = w [n], \ quad & 0 \ leq n \ leq {\ frac {N} {2}} \ end {matriz}} \ right \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab34271ac62f34c531c4d6cc0b8ffd2e9793623a)


![{\ Displaystyle \ left. {\ begin {array} {lll} w [0] = 0, \\ w [n] = \ left (1+ \ exp \ left ({\ frac {\ varepsilon N} {n} } - {\ frac {\ varepsilon N} {\ varepsilon Nn}} \ right) \ right) ^ {- 1}, \ quad & 1 \ leq n <\ varepsilon N \\ w [n] = 1, \ quad & \ varepsilon N \ leq n \ leq {\ frac {N} {2}} \\ w [Nn] = w [n], \ quad & 0 \ leq n \ leq {\ frac {N} {2}} \ end {array}} \ right \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f50bb4690593ab87a47ed71fec1945a3f95b9d0d)




![{\ Displaystyle w [n] = {\ frac {I_ {0} \ left (\ pi \ alpha {\ sqrt {1- \ left ({\ frac {2n} {N}} - 1 \ right) ^ {2 " }}} \ right)} {I_ {0} (\ pi \ alpha)}}, \ quad 0 \ leq n \ leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337ca65bf1465649348a8eb22356662c4188b092)





![{\ Displaystyle w_ {0} [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0d68356ad0cc45bf520fbe5be3266aa7c431cd8)
![{\ Displaystyle W_ {0} [k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af1b9baa4526ac8ec5f39c3cd63782248015037f)





![{\ Displaystyle w [n] = w_ {0} \ left (n - {\ frac {N} {2}} \ right), \ quad 0 \ leq n \ leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3af173b60d19716e14882dabdec080868fa3e0ae)
![{\ Displaystyle {\ begin {alineado} w_ {0} \ left (n - {\ frac {N} {2}} \ right) = {\ frac {1} {N + 1}} \ sum _ {k = 0} ^ {N} W_ {0} (k) \ cdot e ^ {\ frac {i2 \ pi k (nN / 2)} {N + 1}} = {\ frac {1} {N + 1}} \ sum _ {k = 0} ^ {N} \ left [\ left (-e ^ {\ frac {i \ pi} {N + 1}} \ right) ^ {k} \ cdot W_ {0} (k ) \ right] e ^ {\ frac {i2 \ pi kn} {N + 1}}, \ end {alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f3590133d3da32b13aa211153542e96d14a46e)


![{\ Displaystyle w [n] = {\ frac {1} {N + 1}} \ left [C_ {N} ^ {\ mu} (x_ {0}) + \ sum _ {k = 1} ^ {\ frac {N} {2}} C_ {N} ^ {\ mu} \ left (x_ {0} \ cos {\ frac {k \ pi} {N + 1}} \ right) \ cos {\ frac {2n \ pi k} {N + 1}} \ right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe5e8dc43d2c5edbe601e3abf542a177689f4276)







![{\ Displaystyle w [n] = e ^ {- \ left | n - {\ frac {N} {2}} \ right | {\ frac {1} {\ tau}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/141d1630d759c1ebf5120671e36f86a6117f259c)

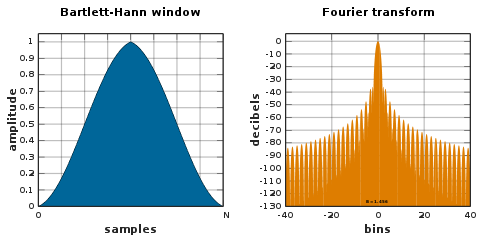
![{\ Displaystyle w [n] = a_ {0} -a_ {1} \ left | {\ frac {n} {N}} - {\ frac {1} {2}} \ right | -a_ {2} \ cos \ left ({\ frac {2 \ pi n} {N}} \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e64d33f0c717a2b40af2ed16c9fff5f58d95b937)




![{\ Displaystyle w [n] = {\ frac {1} {2}} \ left (1- \ cos \ left ({\ frac {2 \ pi n} {N}} \ right) \ right) e ^ { \ frac {- \ alpha \ left | N-2n \ right |} {N}} \, = \ operatorname {hav} \ left ({\ frac {2 \ pi n} {N}} \ right) e ^ { \ frac {- \ alpha \ left | N-2n \ right |} {N}} \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85cca45da54e9171ac868a34aeaa1311d2434e18)


![{\ Displaystyle w_ {0} [n] = a_ {0} + \ sum _ {k = 1} ^ {K} a_ {2k} \ left ({\ frac {n} {\ sigma}} \ right) ^ {2k}, \ quad - {\ frac {N} {2}} \ leq n \ leq {\ frac {N} {2}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0985efd235d3dcfbd7c9a2631aa173cd5c2d4cdf)




![{\ Displaystyle w [n] = \ operatorname {sinc} \ left ({\ frac {2n} {N}} - 1 \ right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/380ec565d5a93c55eb9d1109065556115b5c0f99)






