Axioma de Pasch - Pasch's axiom

No confundir con el teorema de Pasch .

En geometría , el axioma de Pasch es un enunciado en geometría plana , usado implícitamente por Euclides , que no puede derivarse de los postulados que Euclides les dio. Su papel esencial fue descubierto por Moritz Pasch en 1882.

Declaración

Dos líneas (en negro) que se encuentran con un lado del triángulo internamente y se encuentran con los otros lados interna y externamente

El axioma establece que,

Axioma de Pascua  -  Let A , B , C sea tres puntos que no se acuesta en una línea y dejar que un ser una línea en el plano ABC que no cumpla con cualquiera de los puntos A , B , C . Si la recta a pasa por un punto del segmento AB , también pasa por un punto del segmento AC o por un punto del segmento BC .

El hecho de que los segmentos AC y BC no estén ambos intersectados por la línea a se demuestra en el Suplemento I, 1, que fue escrito por P. Bernays .

Una versión más moderna de este axioma es la siguiente:

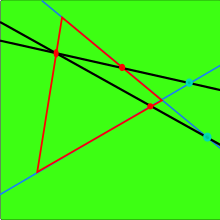
Una versión más moderna del axioma de Pasch  :  en el plano, si una línea interseca un lado de un triángulo internamente, entonces interseca precisamente un otro lado internamente y el tercer lado externamente , si no pasa por un vértice del triángulo.

(En caso de que el tercer lado sea paralelo a nuestra línea, contamos una "intersección en el infinito" como externa). A menudo se ve una versión más informal del axioma:

Una versión más informal del axioma de Pasch  :  si una línea, que no pasa por ningún vértice de un triángulo, se encuentra con un lado del triángulo, entonces se encuentra con otro lado.

Historia

Pasch publicó este axioma en 1882 y mostró que los axiomas de Euclides estaban incompletos. El axioma era parte del enfoque de Pasch para introducir el concepto de orden en la geometría plana.

Equivalencias

En otros tratamientos de geometría elemental, utilizando diferentes conjuntos de axiomas, el axioma de Pasch puede demostrarse como un teorema; es una consecuencia del axioma de separación de planos cuando se toma como uno de los axiomas. Hilbert usa el axioma de Pasch en su tratamiento axiomático de la geometría euclidiana . Dados los axiomas restantes en el sistema de Hilbert, se puede demostrar que el axioma de Pasch es lógicamente equivalente al axioma de separación de planos.

El uso de Hilbert del axioma de Pasch

David Hilbert usa el axioma de Pasch en su libro Foundations of Geometry, que proporciona una base axiomática para la geometría euclidiana. Dependiendo de la edición, se numera II.4 o II.5. Su declaración se da arriba.

En el tratamiento de Hilbert, este axioma aparece en la sección relativa a los axiomas de orden y se denomina axioma plano de orden . Dado que no expresa el axioma en términos de los lados de un triángulo (considerados como líneas en lugar de segmentos de línea), no es necesario hablar de las intersecciones internas y externas de la línea a con los lados del triángulo ABC .

Advertencias

El axioma de Pasch es distinto del teorema de Pasch, que es un enunciado sobre el orden de cuatro puntos en una línea. Sin embargo, en la literatura hay muchos casos en los que se hace referencia al axioma de Pasch como teorema de Pasch. Un ejemplo notable de esto es Greenberg (1974 , p. 67).

El axioma de Pasch no debe confundirse con el axioma de Veblen-Young para la geometría proyectiva , que puede enunciarse como:

Axioma de Veblen-Young para geometría proyectiva  :  si una línea interseca dos lados de un triángulo, también interseca el tercer lado.

No se mencionan las intersecciones internas y externas en el enunciado del axioma de Veblen-Young, que solo se ocupa de la propiedad de incidencia de las líneas que se encuentran. En geometría proyectiva, el concepto de intermediación (necesario para definir lo interno y lo externo) no es válido y todas las líneas se encuentran (por lo que no surge el problema de las líneas paralelas).

Notas

Referencias

  • Beutelspacher, Albrecht; Rosenbaum, Ute (1998), Geometría proyectiva: de los cimientos a las aplicaciones , Cambridge University Press , ISBN 978-0-521-48364-3, MR  1629468
  • Faber, Richard L. (1983), Fundamentos de la geometría euclidiana y no euclidiana , Nueva York: Marcel Dekker, Inc., ISBN 978-0-8247-1748-3
  • Greenberg, Marvin Jay (1974), Geometrías euclidianas y no euclidianas: desarrollo e historia (1a ed.), San Francisco: WH Freeman, ISBN 978-0-7167-0454-6
    • Greenberg, Marvin Jay (2007), geometrías euclidianas y no euclidianas: desarrollo e historia (4a ed.), San Francisco: WH Freeman, ISBN 978-0-7167-9948-1
  • Hilbert, David (1903), Grundlagen der Geometrie (en alemán), Leipzig: BG Teubner
    • Hilbert, David (1950) [1902], The Foundations of Geometry (PDF) , traducido por Townsend, EJ, LaSalle, IL: Open Court Publishing
    • Hilbert, David (1999) [1971], Foundations of Geometry , traducido por Unger, Leo (2ª ed.), LaSalle, IL: Open Court Publishing, ISBN 978-0-87548-164-7
  • Moise, Edwin (1990), Geometría elemental desde un punto de vista avanzado (Tercera ed.), Addison-Wesley, Reading, MA, p. 74, ISBN 978-0-201-50867-3
  • Pambuccian, Victor (2011), "La axiomática de la geometría ordenada: I. Espacios de incidencia ordenados", Expositiones Mathematicae (29): 24–66, doi : 10.1016 / j.exmath.2010.09.004
  • Pasch, Moritz (1912) [primera edición 1882], Vorlesungen uber neuere Geometrie (en alemán) (2ª ed.), Leipzig: BG Teubner
  • Wylie, Jr., Clarence Raymond (1964), Fundamentos de la geometría , Nueva York: McGraw-Hill, ISBN 978-0-070-72191-3
    • Wylie, Jr., CR (2009) [1964], Foundations of Geometry , Mineola, Nueva York: Dover Publications, ISBN 978-0-486-47214-0

enlaces externos