Criterio de Kelly - Kelly criterion

En la teoría de la probabilidad , el criterio de Kelly (o estrategia de Kelly o apuesta de Kelly ) es una fórmula que determina el tamaño teórico óptimo para una apuesta. Es válido cuando se conocen los rendimientos esperados. El tamaño de la apuesta de Kelly se obtiene maximizando el valor esperado del logaritmo de riqueza, que equivale a maximizar la tasa de crecimiento geométrico esperada. Fue descrito por JL Kelly Jr. , un investigador de Bell Labs , en 1956. El criterio también se conoce como el método científico de juego, ya que conduce a una mayor riqueza en comparación con cualquier otra estrategia a largo plazo (es decir, el rendimiento máximo teórico como el número de apuestas va al infinito).

Se ha demostrado el uso práctico de la fórmula para los juegos de azar y se utilizó la misma idea para explicar la diversificación en la gestión de inversiones . En la década de 2000, el análisis al estilo de Kelly se convirtió en parte de la teoría de la inversión convencional y se ha afirmado que los inversores de éxito conocidos, incluidos Warren Buffett y Bill Gross, utilizan los métodos de Kelly. William Poundstone escribió un extenso relato popular de la historia de las apuestas Kelly. Consulte también Elección de cartera intertemporal .

Ejemplo de apuesta óptima

La utilidad del monto de la apuesta de Kelly se puede obtener comparándola con otras estrategias de juego.

En un estudio, a cada participante se le dio $ 25 y se le pidió que hiciera apuestas iguales en una moneda que obtendría cara el 60% de las veces. Los participantes tenían 30 minutos para jugar, por lo que podían realizar unas 300 apuestas y los premios tenían un límite de 250 dólares. La apuesta de Kelly en este escenario es del 20%, lo que equivale a una ganancia promedio del 2% en cada ronda. El promedio de ganancias esperadas con 300 rondas es de $ 10,500 si no estuviera limitado. Pero el comportamiento de los sujetos de prueba estuvo lejos de ser óptimo:

Sorprendentemente, el 28% de los participantes quebró y el pago promedio fue de solo $ 91. Solo el 21% de los participantes alcanzó el máximo. 18 de los 61 participantes apostaron todo en un solo lanzamiento, mientras que dos tercios apostaron a cruz en algún momento del experimento.

Si los apostadores hubieran seguido la apuesta de Kelly, se espera que el 94% de los participantes hubieran alcanzado el límite.

Fórmula de juego

Cuando perder la apuesta implica perder toda la apuesta, la apuesta de Kelly es:

${\ Displaystyle f ^ {*} = p - {\ frac {q} {b}} = p + {\ frac {p-1} {b}}}$

dónde:

• ${\ Displaystyle f ^ {*}}$ es la fracción de los fondos actuales para apostar.
• ${\ Displaystyle p}$ es la probabilidad de ganar.
• ${\ Displaystyle q}$es la probabilidad de una pérdida ( ).${\ Displaystyle q = 1-p}$
• ${\ Displaystyle b}$es la cantidad que se gana con una ganancia. Por ejemplo, si apuesta $ 10 en una apuesta de probabilidades de 2 a 1 , (al ganar, se le devuelven $ 30, ganando $ 20), entonces .${\ Displaystyle b = \ $ 20 / \ $ 10 = 2.0}$

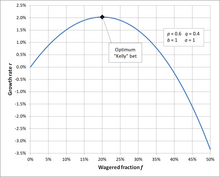
Por ejemplo, si una apuesta tiene un 60% de posibilidades de ganar ( , ), y el jugador recibe probabilidades de 1 a 1 en una apuesta ganadora ( ), entonces el jugador debe apostar el 20% de los fondos en cada oportunidad ( ) , con el fin de maximizar la tasa de crecimiento a largo plazo del bankroll. ${\ Displaystyle p = 0,6}$${\ Displaystyle q = 0.4}$${\ Displaystyle b = 1}$${\ displaystyle f ^ {*} = 0,6 - {\ frac {0,4} {1}} = 0,2}$

Si el jugador tiene ventaja cero, es decir, si , entonces el criterio recomienda que el jugador no apueste nada. ${\ Displaystyle b = q / p}$

Si la ventaja es negativa ( ), la fórmula da un resultado negativo, lo que indica que el jugador debe tomar el otro lado de la apuesta. Por ejemplo, en la ruleta americana , al apostador se le ofrece una recompensa de dinero par ( ) en rojo, cuando hay 18 números rojos y 20 números no rojos en la rueda ( ). La apuesta de Kelly es , lo que significa que el jugador debe apostar un diecinueve de su bankroll a que no saldrá rojo . No se ofrece una apuesta anti-rojo explícita con probabilidades comparables en la ruleta, por lo que lo mejor que puede hacer un jugador de Kelly es no apostar nada. ${\ Displaystyle b <q / p}$${\ Displaystyle b = 1}$${\ displaystyle p = 18/38}$${\ Displaystyle -1/19}$

Fórmula de inversión

Una forma más general de la fórmula de Kelly permite pérdidas parciales, lo que es relevante para las inversiones:

${\ Displaystyle f ^ {*} = {\ frac {p} {a}} - {\ frac {q} {b}}.}$

dónde:

• ${\ Displaystyle f ^ {*}}$ es la fracción de los activos que se aplicará al valor.
• ${\ Displaystyle p}$ es la probabilidad de que la inversión aumente de valor.
• ${\ Displaystyle q}$es la probabilidad de que la inversión disminuya de valor ( ).${\ Displaystyle q = 1-p}$
• ${\ Displaystyle a}$es la fracción que se pierde en un resultado negativo. Por ejemplo, si el precio del valor cae un 10%, entonces${\ Displaystyle a = 0.1}$
• ${\ Displaystyle b}$es la fracción que se gana en un resultado positivo. Por ejemplo, si el precio del valor aumenta un 10%, entonces .${\ Displaystyle b = 0.1}$

Tenga en cuenta que el criterio de Kelly solo es válido para probabilidades de resultado conocidas , lo que no es el caso de las inversiones. No se recomienda invertir la fracción de Kelly completa.

Esta fórmula puede resultar en fracciones de Kelly superiores a 1. En este caso, es teóricamente ventajoso utilizar el apalancamiento para comprar valores adicionales con margen .

Prueba

Las pruebas heurísticas del criterio de Kelly son sencillas. El criterio de Kelly maximiza el valor esperado del logaritmo de riqueza (el valor esperado de una función viene dado por la suma, sobre todos los resultados posibles, de la probabilidad de cada resultado particular multiplicado por el valor de la función en el caso de ese resultado ). Comenzamos con 1 unidad de riqueza y apostamos una fracción de esa riqueza a un resultado que ocurre con probabilidad y ofrece probabilidades de . La probabilidad de ganar es , y en ese caso la riqueza resultante es igual a . La probabilidad de perder es , y en ese caso la riqueza resultante es igual a . Por lo tanto, la tasa de crecimiento geométrico esperada es: ${\ Displaystyle f}$${\ Displaystyle p}$${\ Displaystyle b}$${\ Displaystyle p}$${\ Displaystyle 1 + fb}$${\ Displaystyle q = 1-p}$${\ displaystyle 1-fa}$${\ Displaystyle r}$

${\ Displaystyle r = (1 + fb) ^ {p} \ cdot (1-fa) ^ {q}}$

Queremos encontrar el máximo r de esta curva, lo que implica encontrar la derivada de la ecuación. Esto se logra más fácilmente tomando primero el logaritmo de cada lado. La ecuación resultante es:

${\ Displaystyle E = \ log (r) = p \ log (1 + fb) + q \ log (1-fa)}$

que denota un crecimiento de la riqueza logarítmico. Para encontrar el valor de para el cual se maximiza la tasa de crecimiento, denotado como , diferenciamos la expresión anterior y la igualamos a cero. Esto da: ${\ Displaystyle E}$${\ Displaystyle f}$${\ Displaystyle f ^ {*}}$

${\ Displaystyle \ left. {\ frac {dE} {df}} \ right | _ {f = f ^ {*}} = {\ frac {pb} {1 + f ^ {*} b}} + {\ frac {-qa} {1-f ^ {*} a}} = 0}$

Reordenando esta ecuación para resolver el valor de da el criterio de Kelly: ${\ Displaystyle f ^ {*}}$

${\ Displaystyle f ^ {*} = {\ frac {p} {a}} - {\ frac {q} {b}}}$

Tenga en cuenta que esta expresión se reduce a la fórmula de juego simple cuando , cuando una pérdida resulta en la pérdida total de la apuesta. ${\ Displaystyle a = 1 = 100 \%}$

Bernoulli

En un artículo de 1738, Daniel Bernoulli sugirió que, cuando uno puede elegir entre apuestas o inversiones, debe elegir aquello con la media geométrica más alta de resultados. Esto es matemáticamente equivalente al criterio de Kelly, aunque la motivación es completamente diferente (Bernoulli quería resolver la paradoja de San Petersburgo ).

Un idioma Inglés traducción del artículo de Bernoulli no se publicó hasta 1954, pero el trabajo era bien conocido entre los matemáticos y economistas.

Aplicación al mercado de valores

En finanzas matemáticas, una cartera se denomina crecimiento óptimo si las ponderaciones de los valores maximizan la tasa de crecimiento geométrico esperada (que es equivalente a maximizar la riqueza logarítmica).

Los cálculos de carteras óptimas de crecimiento pueden sufrir tremendos problemas de entrada y salida de basura. Por ejemplo, los casos siguientes dan por sentado el rendimiento esperado y la estructura de covarianza de varios activos, pero estos parámetros se estiman o modelan en el mejor de los casos con una incertidumbre significativa. El desempeño ex post de una cartera supuestamente óptima para el crecimiento puede diferir fantásticamente con la predicción ex ante si las ponderaciones de la cartera están impulsadas en gran medida por errores de estimación. Tratar con la incertidumbre de los parámetros y el error de estimación es un tema importante en la teoría de carteras. Un enfoque para contrarrestar el riesgo desconocido es invertir menos que el criterio de Kelly, por ejemplo, la mitad.

Crítica

Aunque la promesa de la estrategia de Kelly de hacerlo mejor que cualquier otra estrategia a largo plazo parece convincente, algunos economistas han argumentado enérgicamente en su contra, principalmente porque las limitaciones de inversión específicas de un individuo pueden anular el deseo de una tasa de crecimiento óptima. La alternativa convencional es la teoría de la utilidad esperada, que dice que las apuestas deben dimensionarse para maximizar la utilidad esperada del resultado (para un individuo con utilidad logarítmica , la apuesta de Kelly maximiza la utilidad esperada, por lo que no hay conflicto; además, el artículo original de Kelly establece claramente que necesidad de una función de utilidad en el caso de juegos de azar que se juegan un número finito de veces). Incluso los partidarios de Kelly suelen abogar por un Kelly fraccional (apostar una fracción fija de la cantidad recomendada por Kelly) por una variedad de razones prácticas, como desear reducir la volatilidad o protegerse contra errores no deterministas en sus cálculos de ventaja (ventaja).

Matemáticas avanzadas

Para obtener una prueba rigurosa y general, consulte el artículo original de Kelly o algunas de las otras referencias que se enumeran a continuación. Se han publicado algunas correcciones. Damos el siguiente argumento no riguroso para el caso con (una apuesta 50:50 de "dinero par") para mostrar la idea general y proporcionar algunas ideas. Cuando , un apostador de Kelly apuesta por su riqueza inicial , como se muestra arriba. Si ganan, lo han hecho después de una apuesta. Si pierden, lo han hecho . Supongamos que hacen apuestas como esta y ganan tiempos de esta serie de apuestas. La riqueza resultante será: ${\ Displaystyle b = 1}$${\ Displaystyle b = 1}$${\ Displaystyle 2p-1}$${\ Displaystyle W}$${\ Displaystyle 2pW}$${\ Displaystyle 2 (1-p) W}$${\ Displaystyle N}$${\ Displaystyle K}$${\ Displaystyle N}$

${\ Displaystyle 2 ^ {N} p ^ {K} (1-p) ^ {NK} W \ !.}$

Tenga en cuenta que el orden de las ganancias y las pérdidas no afecta la riqueza resultante. Suponga que otro apostador apuesta una cantidad diferente, por un valor de (donde puede ser positivo o negativo). Tendrán después de una victoria y después de una derrota. Después de la misma serie de victorias y derrotas que el apostador Kelly, tendrán: ${\ Displaystyle (2p-1 + \ Delta) W}$${\ Displaystyle \ Delta}$${\ Displaystyle \ Delta}$${\ Displaystyle (2p + \ Delta) W}$${\ Displaystyle [2 (1-p) - \ Delta] W}$

${\ Displaystyle (2p + \ Delta) ^ {K} [2 (1-p) - \ Delta] ^ {NK} W}$

Tome la derivada de esto con respecto a y obtenga: ${\ Displaystyle \ Delta}$

${\ Displaystyle K (2p + \ Delta) ^ {K-1} [2 (1-p) - \ Delta] ^ {NK} W- (NK) (2p + \ Delta) ^ {K} [2 (1-p) ) - \ Delta] ^ {NK-1} W}$

La función se maximiza cuando esta derivada es igual a cero, lo que ocurre en:

${\ Displaystyle K [2 (1-p) - \ Delta] = (NK) (2p + \ Delta)}$

lo que implica que

${\ Displaystyle \ Delta = 2 \ left ({\ frac {K} {N}} - p \ right)}$

pero la proporción de apuestas ganadoras eventualmente convergerá a:

${\ Displaystyle \ lim _ {N \ to + \ infty} {\ frac {K} {N}} = p}$

según la ley débil de los grandes números . Entonces, a largo plazo, la riqueza final se maximiza estableciendo en cero, lo que significa seguir la estrategia de Kelly. Esto ilustra que Kelly tiene un componente tanto determinista como estocástico. Si uno conoce K y N y desea elegir una fracción constante de riqueza para apostar cada vez (de lo contrario, podría hacer trampa y, por ejemplo, apostar cero después de la K- ^ésima victoria sabiendo que el resto de las apuestas perderán), se terminará. hasta con la mayor cantidad de dinero si uno apuesta: ${\ Displaystyle \ Delta}$

${\ Displaystyle \ left (2 {\ frac {K} {N}} - 1 \ right) W}$

cada vez. Esto es cierto ya sea ​​pequeño o grande. La parte de "largo plazo" de Kelly es necesaria porque K no se conoce de antemano, solo que a medida que se hace grande, se acercará . Alguien que apuesta más que Kelly puede hacerlo mejor aunque sea por un tramo; alguien que apuesta menos que Kelly puede hacerlo mejor si es por un tramo, pero a la larga, Kelly siempre gana. La prueba heurística para el caso general procede de la siguiente manera. En una sola prueba, si inviertes la fracción de tu capital, si tu estrategia tiene éxito, tu capital al final de la prueba aumenta en el factor y, de la misma manera, si la estrategia falla, terminas teniendo tu capital disminuido en la factor . Así, al final de las pruebas (con éxitos y fracasos), el capital inicial de $ 1 rinde ${\ Displaystyle N}$${\ Displaystyle N}$${\ Displaystyle K}$${\ Displaystyle pN}$${\ Displaystyle K> pN}$${\ Displaystyle K <pN}$${\ Displaystyle f}$${\ Displaystyle 1-f + f (1 + b) = 1 + fb}$${\ displaystyle 1-fa}$${\ Displaystyle N}$${\ Displaystyle pN}$${\ Displaystyle qN}$

${\ Displaystyle C_ {N} = (1 + fb) ^ {pN} (1-fa) ^ {qN}.}$

Maximizar , y en consecuencia , con respecto a conduce al resultado deseado ${\ Displaystyle \ log (C_ {N}) / N}$${\ Displaystyle C_ {N}}$${\ Displaystyle f}$

${\ Displaystyle f ^ {*} = p / aq / b.}$

Edward O. Thorp proporcionó una discusión más detallada de esta fórmula para el caso general. Allí, se puede observar que la sustitución de por la razón del número de "aciertos" por el número de ensayos implica que el número de ensayos debe ser muy grande, ya que se define como el límite de esta razón como el número de ensayos. va al infinito. En resumen, apostar cada vez probablemente maximizará la tasa de crecimiento de la riqueza solo en el caso de que el número de pruebas sea muy grande y sean las mismas para cada prueba. En la práctica, se trata de jugar el mismo juego una y otra vez, donde la probabilidad de ganar y las probabilidades de pago son siempre las mismas. En la prueba heurística anterior, los éxitos y fracasos son muy probables solo para muy grandes . ${\ Displaystyle p}$${\ Displaystyle p}$${\ Displaystyle f ^ {*}}$${\ Displaystyle p}$${\ Displaystyle b}$${\ Displaystyle pN}$${\ Displaystyle qN}$${\ Displaystyle N}$

Múltiples resultados

El criterio de Kelly puede generalizarse sobre los juegos de azar en muchos resultados mutuamente excluyentes, como en las carreras de caballos. Suponga que hay varios resultados mutuamente excluyentes. La probabilidad de que el -ésimo caballo gane la carrera es , la cantidad total de apuestas realizadas en el -ésimo caballo es , y ${\ Displaystyle k}$${\ Displaystyle p_ {k}}$${\ Displaystyle k}$${\ Displaystyle B_ {k}}$

${\ Displaystyle \ beta _ {k} = {\ frac {B_ {k}} {\ sum _ {i} B_ {i}}} = {\ frac {D} {1 + Q_ {k}}},}$

¿Dónde están las probabilidades de pago? , es la tasa de dividendo donde está la toma de pista o el impuesto, es la tasa de ingresos después de la deducción de la toma de pista cuando gana -th caballo. La fracción de los fondos del apostador para apostar en -ésimo caballo es . El criterio de Kelly para los juegos de azar con múltiples resultados mutuamente excluyentes proporciona un algoritmo para encontrar el conjunto óptimo de resultados por los que es razonable apostar y proporciona una fórmula explícita para encontrar las fracciones óptimas de la riqueza del apostador para apostar en los resultados incluidos en el conjunto óptimo. . El algoritmo para el conjunto óptimo de resultados consta de cuatro pasos. ${\ Displaystyle Q_ {k}}$${\ Displaystyle D = 1-tt}$${\ displaystyle tt}$${\ Displaystyle {\ frac {D} {\ beta _ {k}}}}$${\ Displaystyle k}$${\ Displaystyle k}$${\ Displaystyle f_ {k}}$${\ Displaystyle S ^ {o}}$${\ Displaystyle f_ {k} ^ {o}}$${\ Displaystyle S ^ {o}}$

Paso 1 : Calcule la tasa de ingresos esperada para todos los resultados posibles (o solo para varios de los más prometedores):

${\ Displaystyle er_ {i} = {\ frac {Dp_ {i}} {\ beta _ {i}}} = p_ {i} (Q_ {i} +1)}$

Paso 2 : Reordene los resultados para que la nueva secuencia no aumente. Así será la mejor apuesta.${\ Displaystyle er_ {k}}$${\ Displaystyle er_ {1}}$

Paso 3 : Conjunto (el conjunto vacío), , . Por lo tanto, la mejor apuesta se considerará primero.${\ Displaystyle S = \ varnothing}$${\ Displaystyle k = 1}$${\ Displaystyle R (S) = 1}$${\ Displaystyle er_ {k} = er_ {1}}$

Paso 4 : Repite:

Si luego inserta el resultado -th en el conjunto:, vuelva a calcular de acuerdo con la fórmula: ${\ Displaystyle er_ {k} = {\ frac {D} {\ beta _ {k}}} p_ {k}> R (S)}$${\ Displaystyle k}$${\ Displaystyle S = S \ cup \ {k \}}$${\ Displaystyle R (S)}$

${\ Displaystyle R (S) = {\ frac {D \ sum _ {k \ notin S} p_ {k}} {D- \ sum _ {k \ in S} \ beta _ {k}}}}$ y luego configurar ,${\ Displaystyle k = k + 1}$

De lo contrario, configure y detenga la repetición.${\ Displaystyle S ^ {o} = S}$

Si el conjunto óptimo está vacío, no apueste en absoluto. Si el conjunto de resultados óptimos no está vacío, entonces la fracción óptima por la que apostar -ésimo resultado se puede calcular a partir de esta fórmula: ${\ Displaystyle S ^ {o}}$${\ Displaystyle S ^ {o}}$${\ Displaystyle f_ {k} ^ {o}}$${\ Displaystyle k}$

${\ Displaystyle f_ {i} = p_ {i} - \ beta _ {i} {\ frac {\ sum _ {k \ notin S} p_ {k}} {(D- \ sum _ {k \ in S} \ beta _ {k})}}}$.

Uno puede probar que

${\ Displaystyle R (S ^ {o}) = 1- \ sum _ {i \ in S ^ {o}} {f_ {i} ^ {o}}}$

donde el lado derecho es la tasa de reserva. Por lo tanto, el requisito puede interpretarse de la siguiente manera: -el resultado final se incluye en el conjunto de resultados óptimos si y solo si su tasa de ingresos esperada es mayor que la tasa de reserva. La fórmula para la fracción óptima se puede interpretar como el exceso de la tasa de ingresos esperada de -th caballo sobre la tasa de reserva dividida por los ingresos después de la deducción de la pista cuando gana -th caballo o como el exceso de la probabilidad de -th caballo ganando sobre la tasa de reserva dividido por los ingresos después de la deducción de la pista cuando gana -th caballo. El exponente de crecimiento binario es ${\ Displaystyle er_ {k} = {\ frac {D} {\ beta _ {k}}} p_ {k}> R (S)}$${\ Displaystyle k}$${\ Displaystyle S ^ {o}}$${\ Displaystyle f_ {k} ^ {o}}$${\ Displaystyle k}$${\ Displaystyle k}$${\ Displaystyle k}$${\ Displaystyle k}$

${\ Displaystyle G ^ {o} = \ sum _ {i \ in S} {p_ {i} \ log _ {2} {(er_ {i})}} + (1- \ sum _ {i \ in S } {p_ {i}}) \ log _ {2} {(R (S ^ {o}))},}$

y el tiempo de duplicación es

${\ Displaystyle T_ {d} = {\ frac {1} {G ^ {o}}}.}$

Este método de selección de apuestas óptimas se puede aplicar también cuando las probabilidades se conocen solo para varios de los resultados más prometedores, mientras que los resultados restantes no tienen ninguna posibilidad de ganar. En este caso debe ser que ${\ Displaystyle p_ {k}}$

${\ Displaystyle \ sum _ {i} {p_ {i}} <1,}$ y

${\ Displaystyle \ sum _ {i} {\ beta _ {i}} <1}$.

Inversiones en acciones

El polinomio de Taylor de segundo orden se puede utilizar como una buena aproximación del criterio principal. Principalmente, es útil para la inversión en acciones, donde la fracción dedicada a la inversión se basa en características simples que pueden estimarse fácilmente a partir de datos históricos existentes: valor esperado y varianza . Esta aproximación conduce a resultados que son robustos y ofrecen resultados similares a los del criterio original.

Para activos individuales (acciones, fondos indexados, etc.) y una tasa libre de riesgo, es fácil obtener la fracción óptima para invertir a través del movimiento browniano geométrico . El valor de un activo distribuido lognormalmente en el momento ( ) es ${\ Displaystyle S}$${\ Displaystyle t}$${\ Displaystyle S_ {t}}$

${\ Displaystyle S_ {t} = S_ {0} \ exp \ left (\ left (\ mu - {\ frac {\ sigma ^ {2}} {2}} \ right) t + \ sigma W_ {t} \ right ),}$

de la solución del movimiento browniano geométrico donde es un proceso de Wiener , y (porcentaje de deriva) y (porcentaje de volatilidad) son constantes. Tomando expectativas del logaritmo: ${\ Displaystyle W_ {t}}$${\ Displaystyle \ mu}$${\ Displaystyle \ sigma}$

${\ Displaystyle \ mathbb {E} \ log (S_ {t}) = \ log (S_ {0}) + \ left (\ mu - {\ frac {\ sigma ^ {2}} {2}} \ right) t.}$

Entonces el retorno de registro esperado es ${\ Displaystyle R_ {s}}$

${\ Displaystyle R_ {s} = \ left (\ mu - {\ frac {\ sigma ^ {2}} {2}} \, \ right) s.}$

Para una cartera compuesta por un activo y un bono que paga una tasa libre de riesgo , con una fracción invertida en y en el bono, el rendimiento esperado de un período viene dado por ${\ Displaystyle S}$${\ Displaystyle r}$${\ Displaystyle f}$${\ Displaystyle S}$${\ Displaystyle (1-f)}$

${\ Displaystyle \ mathbb {E} \ left (f \ left [{\ frac {S_ {1}} {S_ {0}}} - 1 \ right] + (1-f) r \ right) = \ mathbb { E} \ left (f \ left [\ exp \ left (\ left (\ mu - {\ frac {\ sigma ^ {2}} {2}} \ right) + \ sigma W_ {1} \ right) -1 \ derecha] \ derecha) + (1-f) r}$

sin embargo, la gente parece lidiar con el retorno de registro esperado durante un período en el contexto de Kelly: ${\ Displaystyle G (f)}$

${\ Displaystyle G (f) = f \ mu - {\ frac {(f \ sigma) ^ {2}} {2}} + ((1-f) \ r).}$

Resolviendo obtenemos ${\ Displaystyle \ max (G (f))}$

${\ Displaystyle f ^ {*} = {\ frac {\ mu -r} {\ sigma ^ {2}}}.}$

${\ Displaystyle f ^ {*}}$es la fracción que maximiza el retorno logarítmico esperado y, por tanto, es la fracción de Kelly. Thorp llegó al mismo resultado pero a través de una derivación diferente. Recuerde que es diferente a la devolución del registro de activos . Confundir esto es un error común que cometen los sitios web y los artículos que hablan sobre el Criterio de Kelly. ${\ Displaystyle \ mu}$${\ Displaystyle R_ {s}}$

Para múltiples activos, considere un mercado con las acciones correlacionadas con retornos estocásticos , y un bono sin riesgo con el regreso . Un inversor pone una fracción de su capital y el resto se invierte en el bono. Sin pérdida de generalidad, suponga que el capital inicial del inversor es igual a 1. De acuerdo con el criterio de Kelly, se debe maximizar ${\ Displaystyle n}$${\ Displaystyle S_ {k}}$${\ Displaystyle r_ {k}}$${\ Displaystyle k = 1, ..., n,}$${\ Displaystyle r}$${\ Displaystyle u_ {k}}$${\ Displaystyle S_ {k}}$

${\ Displaystyle \ mathbb {E} \ left [\ ln \ left ((1 + r) + \ sum \ limits _ {k = 1} ^ {n} u_ {k} (r_ {k} -r) \ right )\Derecha].}$

La expansión de este con una serie de Taylor alrededor obtenemos ${\ Displaystyle {\ vec {u_ {0}}} = (0, \ ldots, 0)}$

${\ Displaystyle \ mathbb {E} \ left [\ ln (1 + r) + \ sum \ limits _ {k = 1} ^ {n} {\ frac {u_ {k} (r_ {k} -r)} {1 + r}} - {\ frac {1} {2}} \ suma \ límites _ {k = 1} ^ {n} \ suma \ límites _ {j = 1} ^ {n} u_ {k} u_ {j} {\ frac {(r_ {k} -r) (r_ {j} -r)} {(1 + r) ^ {2}}} \ derecha].}$

Por lo tanto, reducimos el problema de optimización a la programación cuadrática y la solución sin restricciones es

${\ Displaystyle {\ vec {u ^ {\ star}}} = (1 + r) ({\ widehat {\ Sigma}}) ^ {- 1} ({\ widehat {\ vec {r}}} - r )}$

donde y son el vector de medias y la matriz de segundos momentos mixtos no centrales de los rendimientos en exceso. También hay un algoritmo numérico para las estrategias de Kelly fraccionarias y para la solución óptima sin apalancamiento y sin restricciones de venta en corto. ${\ Displaystyle {\ widehat {\ vec {r}}}}$${\ Displaystyle {\ widehat {\ Sigma}}}$

Ver también

• Riesgo de ruina
• Teoría del juego y la información
• La paradoja de Proebsting
• El problema de la cartera de Merton

Referencias

enlaces externos