Jerarquía aritmética - Arithmetical hierarchy

Una ilustración de cómo interactúan los niveles de la jerarquía y dónde se encuentran algunas categorías de conjuntos básicos dentro de ella.

En la lógica matemática , la jerarquía aritmética , jerarquía aritmética o jerarquía de Kleene-Mostowski (después matemáticos Stephen Cole Kleene y Andrzej Mostowski ) clasifica ciertos conjuntos basados en la complejidad de las fórmulas que los definen. Cualquier conjunto que reciba una clasificación se llama aritmético .

La jerarquía aritmética es importante en la teoría de la recursividad , la teoría descriptiva de conjuntos efectiva y el estudio de teorías formales como la aritmética de Peano .

El algoritmo de Tarski-Kuratowski proporciona una manera fácil de obtener un límite superior en las clasificaciones asignadas a una fórmula y el conjunto que define.

La jerarquía hiperaritmética y la jerarquía analítica amplían la jerarquía aritmética para clasificar fórmulas y conjuntos adicionales.

La jerarquía aritmética de fórmulas.

La jerarquía aritmética asigna clasificaciones a las fórmulas en el lenguaje de la aritmética de primer orden . Las clasificaciones se indican y para números naturales n (incluido 0). Las letras griegas aquí son símbolos de cara clara , lo que indica que las fórmulas no contienen parámetros establecidos. ${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$

Si una fórmula es lógicamente equivalente a una fórmula con solo cuantificadores acotados , se le asignan las clasificaciones y . ${\ Displaystyle \ phi}$${\ Displaystyle \ phi}$${\ Displaystyle \ Sigma _ {0} ^ {0}}$${\ Displaystyle \ Pi _ {0} ^ {0}}$

Las clasificaciones y se definen inductivamente para cada número natural n usando las siguientes reglas: ${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$

• Si es lógicamente equivalente a una fórmula de la forma , donde es , entonces se le asigna la clasificación .${\ Displaystyle \ phi}$${\ estilo de visualización \ existe m_ {1} \ existe m_ {2} \ cdots \ existe m_ {k} \ psi}$${\ Displaystyle \ psi}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ phi}$${\ Displaystyle \ Sigma _ {n + 1} ^ {0}}$
• Si es lógicamente equivalente a una fórmula de la forma , donde es , entonces se le asigna la clasificación .${\ Displaystyle \ phi}$${\ Displaystyle \ forall m_ {1} \ forall m_ {2} \ cdots \ forall m_ {k} \ psi}$${\ Displaystyle \ psi}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ phi}$${\ Displaystyle \ Pi _ {n + 1} ^ {0}}$

Una fórmula es equivalente a una fórmula que comienza con algunos cuantificadores existenciales y alterna tiempos entre series de cuantificadores existenciales y universales ; mientras que una fórmula es equivalente a una fórmula que comienza con algunos cuantificadores universales y se alterna de forma análoga. ${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle n-1}$${\ Displaystyle \ Pi _ {n} ^ {0}}$

Debido a que cada fórmula de primer orden tiene una forma normal prenex , a cada fórmula se le asigna al menos una clasificación. Debido a que se pueden agregar cuantificadores redundantes a cualquier fórmula, una vez que a una fórmula se le asigna la clasificación o se le asignarán las clasificaciones y para cada r> n . La única clasificación relevante asignada a una fórmula es, por tanto, la que tiene el mínimo de n ; todas las demás clasificaciones se pueden determinar a partir de él. ${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {r} ^ {0}}$${\ Displaystyle \ Pi _ {r} ^ {0}}$

La jerarquía aritmética de conjuntos de números naturales.

Un conjunto X de números naturales se define mediante la fórmula φ en el lenguaje de la aritmética de Peano (el lenguaje de primer orden con símbolos "0" para cero, "S" para la función sucesora, "+" para suma, "×" para multiplicación , y "=" para la igualdad), si los elementos de X son exactamente los números que satisfacen φ. Es decir, para todos los números naturales n ,

${\ Displaystyle n \ in X \ Leftrightarrow \ mathbb {N} \ models \ varphi ({\ underline {n}}),}$

donde es el numeral en el lenguaje aritmético correspondiente a . Un conjunto es definible en aritmética de primer orden si está definido por alguna fórmula en el lenguaje de la aritmética de Peano. ${\ Displaystyle {\ underline {n}}}$${\ Displaystyle n}$

Cada conjunto X de los números naturales que es definible en la aritmética de primer orden se asigna clasificaciones de la forma , y , donde es un número natural, como sigue. Si X es definible por una fórmula a continuación, X se le asigna la clasificación . Si X es definible por una fórmula a continuación, X se le asigna la clasificación . Si X es ambos y luego se le asigna la clasificación adicional . ${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$${\ Displaystyle n}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle X}$${\ Displaystyle \ Delta _ {n} ^ {0}}$

Tenga en cuenta que rara vez tiene sentido hablar de fórmulas; el primer cuantificador de una fórmula es existencial o universal. Entonces, un conjunto no está definido por una fórmula; más bien, existen fórmulas y que definen el conjunto. Por ejemplo, el conjunto de números naturales impares se puede definir mediante o . ${\ Displaystyle \ Delta _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle n}$${\ Displaystyle \ forall k (n \ neq 2 \ times k)}$${\ Displaystyle \ existe k (n = 2 \ times k + 1)}$

Se utiliza una definición paralela para definir la jerarquía aritmética de las potencias cartesianas finitas del conjunto de números naturales. En lugar de fórmulas con una variable libre, se utilizan fórmulas con k variables de números libres para definir la jerarquía aritmética en conjuntos de k - tuplas de números naturales. De hecho, estos están relacionados mediante el uso de una función de emparejamiento .

Jerarquías aritméticas relativizadas

Así como podemos definir lo que significa para un conjunto X sea recursiva en relación con otro conjunto Y permitiendo que el cálculo definiendo X consultar Y como un oráculo podemos extender esta noción a toda la jerarquía aritmética y definir lo que significa para X a ser , o en Y , denotados respectivamente y . Para hacerlo, corrija un conjunto de enteros Y y agregue un predicado para la pertenencia a Y al lenguaje de la aritmética de Peano. Entonces decimos que X está en si está definido por una fórmula en este lenguaje expandido. En otras palabras, X es si está definida por una fórmula permitió hacer preguntas acerca de la pertenencia a Y . Alternativamente, se pueden ver los conjuntos como aquellos conjuntos que se pueden construir comenzando con conjuntos recursivos en Y y tomando alternativamente uniones e intersecciones de estos conjuntos hasta n veces. ${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0, Y}}$ ${\ Displaystyle \ Delta _ {n} ^ {0, Y}}$${\ Displaystyle \ Pi _ {n} ^ {0, Y}}$${\ Displaystyle \ Sigma _ {n} ^ {0, Y}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0, Y}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0, Y}}$

Por ejemplo, sea Y un conjunto de números enteros. Sea X el conjunto de números divisibles por un elemento de Y. Entonces X está definido por la fórmula, por lo que X está adentro ( en realidad también está adentro , ya que podríamos unir ambos cuantificadores por n). ${\ Displaystyle \ phi (n) = \ existe m \ existe t (Y (m) \ land m \ times t = n)}$${\ Displaystyle \ Sigma _ {1} ^ {0, Y}}$${\ Displaystyle \ Delta _ {0} ^ {0, Y}}$

Reducibilidad aritmética y grados

La reducibilidad aritmética es una noción intermedia entre la reducibilidad de Turing y la reducibilidad hiperaritmética .

Un conjunto es aritmético (también aritmético y aritméticamente definible ) si está definido por alguna fórmula en el lenguaje de la aritmética de Peano. De manera equivalente, X es aritmética si X es o para algún número entero n . Un conjunto X es aritmético en un conjunto Y , denota , si X es definible como una fórmula en el lenguaje de la aritmética de Peano ampliado por un predicado para ser miembro de Y . De manera equivalente, X es aritmética en Y si X está en o para algún número entero n . Un sinónimo para es: X es aritméticamente reducible a Y . ${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$ ${\ Displaystyle X \ leq _ {A} Y}$${\ Displaystyle \ Sigma _ {n} ^ {0, Y}}$${\ Displaystyle \ Pi _ {n} ^ {0, Y}}$${\ Displaystyle X \ leq _ {A} Y}$

La relación es reflexiva y transitiva, y por tanto la relación definida por la regla ${\ Displaystyle X \ leq _ {A} Y}$${\ Displaystyle \ equiv _ {A}}$

${\ Displaystyle X \ equiv _ {A} Y \ Leftrightarrow X \ leq _ {A} Y \ land Y \ leq _ {A} X}$

es una relación de equivalencia. Las clases de equivalencia de esta relación se denominan grados aritméticos ; están parcialmente ordenados debajo . ${\ Displaystyle \ leq _ {A}}$

La jerarquía aritmética de subconjuntos del espacio de Cantor y Baire

El espacio de Cantor , denotado , es el conjunto de todas las secuencias infinitas de ceros y unos; el espacio de Baire , denotado o , es el conjunto de todas las secuencias infinitas de números naturales. Tenga en cuenta que los elementos del espacio de Cantor se pueden identificar con conjuntos de números enteros y los elementos del espacio de Baire con funciones de enteros a enteros. ${\ Displaystyle 2 ^ {\ omega}}$${\ Displaystyle \ omega ^ {\ omega}}$${\ Displaystyle {\ mathcal {N}}}$

La axiomatización ordinaria de la aritmética de segundo orden utiliza un lenguaje basado en conjuntos en el que los cuantificadores de conjuntos pueden verse naturalmente como cuantificadores en el espacio de Cantor. A un subconjunto del espacio de Cantor se le asigna la clasificación si se puede definir mediante una fórmula. Al conjunto se le asigna la clasificación si se puede definir mediante una fórmula. Si el conjunto es ambos y entonces se le da la clasificación adicional . Por ejemplo, sea ​​el conjunto de todas las cadenas binarias infinitas que no son todas 0 (o, de manera equivalente, el conjunto de todos los conjuntos de enteros no vacíos). Como vemos, eso se define mediante una fórmula y, por tanto, es un conjunto. ${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$${\ Displaystyle O \ subset 2 ^ {\ omega}}$${\ Displaystyle O = \ {X \ in 2 ^ {\ omega} | \ existe n (X (n) = 1) \}}$${\ Displaystyle O}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$

Tenga en cuenta que aunque tanto los elementos del espacio de Cantor (considerados como conjuntos de números enteros) como los subconjuntos del espacio de Cantor se clasifican en jerarquías aritméticas, estos no son la misma jerarquía. De hecho, la relación entre las dos jerarquías es interesante y no trivial. Por ejemplo, los elementos del espacio de Cantor no son (en general) los mismos que los elementos del espacio de Cantor, por lo que es un subconjunto del espacio de Cantor. Sin embargo, muchos resultados interesantes relacionan las dos jerarquías. ${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle X}$${\ Displaystyle \ {X \}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$

Hay dos formas de clasificar un subconjunto del espacio de Baire en la jerarquía aritmética.

• Un subconjunto del espacio de Baire tiene un subconjunto correspondiente del espacio de Cantor debajo del mapa que lleva cada función de a a la función característica de su gráfico. A un subconjunto del espacio de Baire se le da la clasificación , o si y solo si el subconjunto correspondiente del espacio de Cantor tiene la misma clasificación.${\ Displaystyle \ omega}$${\ Displaystyle \ omega}$${\ Displaystyle \ Sigma _ {n} ^ {1}}$${\ Displaystyle \ Pi _ {n} ^ {1}}$${\ Displaystyle \ Delta _ {n} ^ {1}}$
• Se da una definición equivalente de la jerarquía analítica en el espacio de Baire definiendo la jerarquía analítica de fórmulas utilizando una versión funcional de la aritmética de segundo orden; entonces la jerarquía analítica en subconjuntos del espacio de Cantor se puede definir a partir de la jerarquía en el espacio de Baire. Esta definición alternativa da exactamente las mismas clasificaciones que la primera definición.

Se utiliza una definición paralela para definir la jerarquía aritmética en potencias cartesianas finitas del espacio de Baire o del espacio de Cantor, utilizando fórmulas con varias variables libres. La jerarquía aritmética se puede definir en cualquier espacio polaco efectivo ; la definición es particularmente simple para el espacio de Cantor y el espacio de Baire porque encajan con el lenguaje de la aritmética ordinaria de segundo orden.

Tenga en cuenta que también podemos definir la jerarquía aritmética de subconjuntos de los espacios de Cantor y Baire en relación con algún conjunto de números enteros. De hecho negrita es sólo la unión de para todos los conjuntos de enteros Y . Tenga en cuenta que la jerarquía en negrita es solo la jerarquía estándar de los conjuntos de Borel . ${\ Displaystyle \ mathbf {\ Sigma} _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0, Y}}$

Extensiones y variaciones

Es posible definir la jerarquía aritmética de fórmulas utilizando un lenguaje extendido con un símbolo de función para cada función recursiva primitiva . Esta variación cambia ligeramente la clasificación de , ya que el uso de funciones recursivas primitivas en la aritmética de Peano de primer orden requiere, en general, un cuantificador existencial ilimitado y, por lo tanto, algunos conjuntos que están incluidos en esta definición están incluidos en la definición dada al principio de este artículo. artículo. y así todas las clases superiores de la jerarquía no se ven afectadas. ${\ Displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ Displaystyle \ Sigma _ {0} ^ {0}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$

Se puede definir una variación más semántica de la jerarquía en todas las relaciones finitarias de los números naturales; se utiliza la siguiente definición. Toda relación computable se define como . Las clasificaciones y se definen inductivamente con las siguientes reglas. ${\ Displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$

• Si la relación es, entonces la relación se define como${\ Displaystyle R (n_ {1}, \ ldots, n_ {l}, m_ {1}, \ ldots, m_ {k}) \,}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle S (n_ {1}, \ ldots, n_ {l}) = \ forall m_ {1} \ cdots \ forall m_ {k} R (n_ {1}, \ ldots, n_ {l}, m_ { 1}, \ ldots, m_ {k})}$${\ Displaystyle \ Pi _ {n + 1} ^ {0}}$
• Si la relación es, entonces la relación se define como${\ Displaystyle R (n_ {1}, \ ldots, n_ {l}, m_ {1}, \ ldots, m_ {k}) \,}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle S (n_ {1}, \ ldots, n_ {l}) = \ existe m_ {1} \ cdots \ existe m_ {k} R (n_ {1}, \ ldots, n_ {l}, m_ { 1}, \ ldots, m_ {k})}$${\ Displaystyle \ Sigma _ {n + 1} ^ {0}}$

Esta variación cambia ligeramente la clasificación de algunos conjuntos. En particular, como clase de conjuntos (definible por las relaciones en la clase), es idéntico a como se definió anteriormente este último. Puede extenderse para cubrir relaciones finitarias sobre los números naturales, el espacio de Baire y el espacio de Cantor. ${\ Displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ Displaystyle \ Delta _ {1} ^ {0}}$

Significado de la notación

Los siguientes significados se pueden adjuntar a la notación de la jerarquía aritmética en fórmulas.

El subíndice en los símbolos e indica el número de alternancias de bloques de cuantificadores numéricos universales y existenciales que se utilizan en una fórmula. Además, el bloque más externo es existencial en fórmulas y universal en fórmulas. ${\ Displaystyle n}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$

El superíndice en los símbolos , e indica el tipo de objetos sobre los que se cuantifica. Los objetos de tipo 0 son números naturales y los objetos de tipo son funciones que asignan el conjunto de objetos de tipo a los números naturales. La cuantificación sobre objetos de tipo superior, como funciones de números naturales a números naturales, se describe con un superíndice mayor que 0, como en la jerarquía analítica . El superíndice 0 indica cuantificadores sobre números, el superíndice 1 indicaría cuantificación sobre funciones de números a números (objetos tipo 1), el superíndice 2 correspondería a cuantificación sobre funciones que toman un objeto tipo 1 y devuelven un número, y así sucesivamente. ${\ Displaystyle 0}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$${\ Displaystyle i + 1}$${\ Displaystyle i}$

Ejemplos de

• Los conjuntos de números son los que se pueden definir mediante una fórmula de la forma donde solo tiene cuantificadores acotados. Estos son exactamente los conjuntos enumerables de forma recursiva .${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ existe n_ {1} \ cdots \ existe n_ {k} \ psi (n_ {1}, \ ldots, n_ {k}, m)}$${\ Displaystyle \ psi}$
• El conjunto de números naturales que son índices para las máquinas de Turing que calculan funciones totales es . Intuitivamente, un índice cae en este conjunto si y solo si para cada "hay tal que la máquina de Turing con índice se detiene en la entrada después de los pasos". Una prueba completa mostraría que la propiedad que se muestra entre comillas en la oración anterior se puede definir en el lenguaje de la aritmética de Peano mediante una fórmula.${\ Displaystyle \ Pi _ {2} ^ {0}}$${\ Displaystyle e}$${\ Displaystyle m}$${\ Displaystyle s}$${\ Displaystyle e}$${\ Displaystyle m}$${\ Displaystyle s}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$
• Cada subconjunto del espacio de Baire o del espacio de Cantor es un conjunto abierto en la topología habitual del espacio. Además, para cualquier conjunto de este tipo hay una enumeración computable de los números de Gödel de conjuntos abiertos básicos cuya unión es el conjunto original. Por esta razón, los conjuntos a veces se denominan efectivamente abiertos . De manera similar, todos los conjuntos están cerrados y, a veces, los conjuntos se denominan efectivamente cerrados .${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ Pi _ {1} ^ {0}}$${\ Displaystyle \ Pi _ {1} ^ {0}}$
• Cada subconjunto aritmético del espacio de Cantor o del espacio de Baire es un conjunto de Borel . La jerarquía de Borel de Lightface amplía la jerarquía aritmética para incluir conjuntos de Borel adicionales. Por ejemplo, cada subconjunto del espacio de Cantor o Baire es un conjunto (es decir, un conjunto que es igual a la intersección de innumerables conjuntos abiertos). Además, cada uno de estos conjuntos abiertos es y la lista de números de Gödel de estos conjuntos abiertos tiene una enumeración computable. Si es una fórmula con una variable X de conjunto libre y variables de número libre, entonces el conjunto es la intersección de los conjuntos de la forma como n rangos sobre el conjunto de números naturales.${\ Displaystyle \ Pi _ {2} ^ {0}}$${\ Displaystyle G _ {\ delta}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ phi (X, n, m)}$${\ Displaystyle \ Sigma _ {0} ^ {0}}$${\ Displaystyle n, m}$${\ Displaystyle \ Pi _ {2} ^ {0}}$${\ Displaystyle \ {X \ mid \ forall n \ existe m \ phi (X, n, m) \}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ {X \ mid \ existe m \ phi (X, n, m) \}}$
• Las fórmulas se pueden verificar repasando todos los casos uno por uno, lo cual es posible porque todos sus cuantificadores están acotados. El tiempo para esto es polinomio en sus argumentos (por ejemplo, polinomio en n para ); por tanto, sus problemas de decisión correspondientes se incluyen en E (ya que n es exponencial en su número de bits). Esto ya no se cumple con definiciones alternativas de , que permiten el uso de funciones recursivas primitivas, ya que ahora los cuantificadores pueden estar vinculados por cualquier función recursiva primitiva de los argumentos.${\ Displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ Displaystyle \ varphi (n)}$${\ Displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$
• Las fórmulas bajo una definición alternativa, que permite el uso de funciones recursivas primitivas con cuantificadores acotados, corresponden a conjuntos de enteros de la forma de una función recursiva primitiva f . Esto se debe a que permitir un cuantificador acotado no agrega nada a la definición: para una f recursiva primitiva , es lo mismo que , y es lo mismo que ; con la recursividad de curso de valores, cada uno de estos se puede definir mediante una única función de recursión primitiva.${\ Displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0}}$${\ Displaystyle \ {n: f (n) = 0 \}}$${\ Displaystyle \ forall k <n: f (k) = 0}$${\ Displaystyle f (0) + f (1) + ... f (n) = 0}$${\ Displaystyle \ existe k <n: f (k) = 0}$${\ Displaystyle f (0) * f (1) * ... f (n) = 0}$

Propiedades

Las siguientes propiedades son válidas para la jerarquía aritmética de conjuntos de números naturales y la jerarquía aritmética de subconjuntos del espacio de Cantor o Baire.

• Las colecciones y están cerradas bajo uniones finitas e intersecciones finitas de sus respectivos elementos.${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$
• Un conjunto es si y solo si su complemento es . Un conjunto es si y solo si el conjunto es ambos y , en cuyo caso su complemento también lo será .${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$
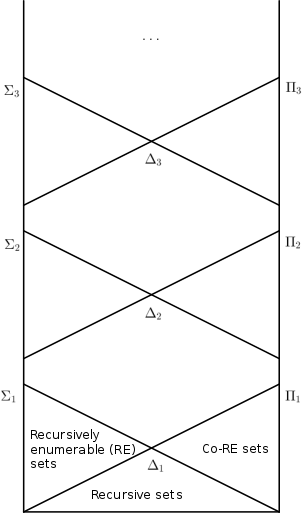
• Las inclusiones y aguantan para todos . Por tanto, la jerarquía no se derrumba. Ésta es una consecuencia directa del teorema de Post .${\ Displaystyle \ Pi _ {n} ^ {0} \ subsetneq \ Pi _ {n + 1} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0} \ subsetneq \ Sigma _ {n + 1} ^ {0}}$${\ Displaystyle n}$
• Las inclusiones , y espere .${\ Displaystyle \ Delta _ {n} ^ {0} \ subsetneq \ Pi _ {n} ^ {0}}$${\ Displaystyle \ Delta _ {n} ^ {0} \ subsetneq \ Sigma _ {n} ^ {0}}$${\ Displaystyle \ Sigma _ {n} ^ {0} \ cup \ Pi _ {n} ^ {0} \ subsetneq \ Delta _ {n + 1} ^ {0}}$${\ Displaystyle n \ geq 1}$

• Por ejemplo, para una máquina de Turing universal T, el conjunto de pares (n, m) tal que T se detiene en n pero no en m, está en (siendo computable con un oráculo para el problema de la detención) pero no en ,.${\ Displaystyle \ Delta _ {2} ^ {0}}$${\ Displaystyle \ Sigma _ {1} ^ {0} \ cup \ Pi _ {1} ^ {0}}$
• ${\ Displaystyle \ Sigma _ {0} ^ {0} = \ Pi _ {0} ^ {0} = \ Delta _ {0} ^ {0} = \ Sigma _ {0} ^ {0} \ cup \ Pi _ {0} ^ {0} \ subconjunto \ Delta _ {1} ^ {0}}$. La inclusión es estricta por la definición dada en este artículo, pero una identidad con se mantiene bajo una de las variaciones de la definición dada arriba .${\ Displaystyle \ Delta _ {1} ^ {0}}$

Relación con las máquinas de Turing

Conjuntos computables

Si S es un conjunto computable de Turing , entonces tanto S como su complemento son recursivamente enumerables (si T es una máquina de Turing que da 1 para las entradas en S y 0 de lo contrario, podemos construir una máquina de Turing que se detenga solo en el primero, y otra que se detenga solo en este último).

Según el teorema de Post , tanto S como su complemento están en . Esto significa que S está tanto dentro como dentro y , por tanto, está dentro . ${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$${\ Displaystyle \ Pi _ {1} ^ {0}}$${\ Displaystyle \ Delta _ {1} ^ {0}}$

De manera similar, para cada conjunto S en , tanto S como su complemento están adentro y, por lo tanto, (según el teorema de Post ) son enumerables de manera recursiva por algunas máquinas de Turing T ₁ y T ₂ , respectivamente. Para cada número n, exactamente uno de estos se detiene. Por lo tanto, podemos construir una máquina de Turing T que alterne entre T ₁ y T ₂ , deteniéndose y devolviendo 1 cuando el primero se detiene o deteniéndose y devolviendo 0 cuando el último se detiene. Por lo tanto, T se detiene en cada ny devuelve si está en S, por lo que S es calculable. ${\ Displaystyle \ Delta _ {1} ^ {0}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$

Resumen de los principales resultados

Los conjuntos computables de Turing de números naturales son exactamente los conjuntos a nivel de la jerarquía aritmética. Los conjuntos recursivamente enumerables son exactamente los conjuntos a nivel . ${\ Displaystyle \ Delta _ {1} ^ {0}}$${\ Displaystyle \ Sigma _ {1} ^ {0}}$

Ninguna máquina de oráculo es capaz de resolver su propio problema de detención (se aplica una variación de la prueba de Turing). El problema de la detención de un oráculo, de hecho, se asienta . ${\ Displaystyle \ Delta _ {n} ^ {0, Y}}$${\ Displaystyle \ Sigma _ {n + 1} ^ {0, Y}}$

El teorema de Post establece una estrecha conexión entre la jerarquía aritmética de conjuntos de números naturales y los grados de Turing . En particular, establece los siguientes hechos para todo n ≥ 1:

• El conjunto (el n º de Turing salto del conjunto vacío) es mucho-uno completa en .${\ Displaystyle \ emptyset ^ {(n)}}$${\ Displaystyle \ Sigma _ {n} ^ {0}}$
• El conjunto es completo en varios .${\ Displaystyle \ mathbb {N} \ setminus \ emptyset ^ {(n)}}$${\ Displaystyle \ Pi _ {n} ^ {0}}$
• El conjunto se Turing completa en .${\ Displaystyle \ emptyset ^ {(n-1)}}$${\ Displaystyle \ Delta _ {n} ^ {0}}$

La jerarquía polinomial es una versión "factible limitada por recursos" de la jerarquía aritmética en la que los límites de longitud polinomial se colocan en los números involucrados (o, de manera equivalente, los límites de tiempo polinomial se colocan en las máquinas de Turing involucradas). Da una clasificación más fina de algunos conjuntos de números naturales que se encuentran al nivel de la jerarquía aritmética. ${\ Displaystyle \ Delta _ {1} ^ {0}}$

Relación con otras jerarquías

Ver también

• Jerarquía de Lévy
• Jerarquía (matemáticas)
• Lógica de interpretabilidad
• Jerarquía polinomial

Referencias