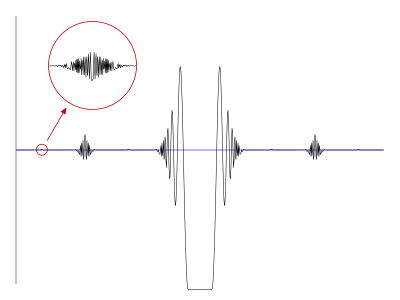
Función de Volterra - Volterra's function
En matemáticas , la función de Volterra , llamada así por Vito Volterra , es una función de valor real V definida en la línea real R con la siguiente curiosa combinación de propiedades:
- V es diferenciable en todas partes
- La derivada V ′ está acotada en todas partes
- La derivada no es integrable de Riemann .
Definición y construcción
La función se define mediante la utilización del conjunto de Smith-Volterra-Cantor y "copias" de la función definida por para y . La construcción de V comienza determinando el valor más grande de x en el intervalo [0, 1/8] para el cual f ′ ( x ) = 0. Una vez que se determina este valor (digamos x 0 ), extienda la función hacia la derecha con un valor constante de f ( x 0 ) hasta el punto 1/8 inclusive. Una vez hecho esto, se puede crear una imagen especular de la función comenzando en el punto 1/4 y extendiéndose hacia abajo hacia 0. Esta función se definirá como 0 fuera del intervalo [0, 1/4]. Luego, traducimos esta función al intervalo [3/8, 5/8] de modo que la función resultante, que llamamos f 1 , sea distinta de cero solo en el intervalo medio del complemento del conjunto de Smith-Volterra-Cantor. Para construir f 2 , f ′ se considera en el intervalo más pequeño [0,1 / 32], se trunca en el último lugar donde la derivada es cero, se extiende y se refleja de la misma manera que antes, y dos copias traducidas de la función resultante se suman af 1 para producir la función f 2 . La función de Volterra resulta entonces al repetir este procedimiento para cada intervalo eliminado en la construcción del conjunto Smith-Volterra-Cantor; en otras palabras, la función V es el límite de la secuencia de funciones f 1 , f 2 , ...
Otras propiedades
La función de Volterra es diferenciable en todas partes tal como lo es f (como se define arriba). Se puede demostrar que f ′ ( x ) = 2 x sin (1 / x ) - cos (1 / x ) para x ≠ 0, lo que significa que en cualquier vecindario de cero, hay puntos donde f ′ toma valores 1 y - 1. Por lo tanto, hay puntos donde V ′ toma valores 1 y −1 en cada vecindario de cada uno de los puntos finales de los intervalos eliminados en la construcción del conjunto S de Smith-Volterra-Cantor . De hecho, V ′ es discontinuo en cada punto de S , aunque V en sí mismo es diferenciable en cada punto de S , con derivada 0. Sin embargo, V ′ es continuo en cada intervalo eliminado en la construcción de S , por lo que el conjunto de discontinuidades de V 'es igual a S .
Dado que el conjunto S de Smith-Volterra-Cantor tiene una medida de Lebesgue positiva , esto significa que V ′ es discontinuo en un conjunto de medidas positivas. Según el criterio de Lebesgue para la integrabilidad de Riemann , V ′ no es integrable de Riemann. Si se repitiera la construcción de la función de Volterra con la medida ordinaria-0 Cantor conjunto C en lugar del conjunto de Cantor "gordo" (medida positiva) S , se obtendría una función con muchas propiedades similares, pero la derivada entonces ser discontinua en el conjunto C de medida 0 en lugar del conjunto S de medida positiva , por lo que la función resultante tendría una derivada integrable de Riemann.