Regresión segmentada - Segmented regression
| Parte de una serie sobre |
| Análisis de regresión |
|---|
| Modelos |
| Estimacion |
| Fondo |
La regresión segmentada , también conocida como regresión por partes o regresión de varilla rota , es un método en el análisis de regresión en el que la variable independiente se divide en intervalos y un segmento de línea separado se ajusta a cada intervalo. El análisis de regresión segmentado también se puede realizar en datos multivariados dividiendo las diversas variables independientes. La regresión segmentada es útil cuando las variables independientes, agrupadas en diferentes grupos, exhiben diferentes relaciones entre las variables en estas regiones. Los límites entre los segmentos son puntos de interrupción .
La regresión lineal segmentada es una regresión segmentada mediante la cual las relaciones en los intervalos se obtienen mediante regresión lineal .
Regresión lineal segmentada, dos segmentos
La regresión lineal segmentada con dos segmentos separados por un punto de corte puede ser útil para cuantificar un cambio abrupto de la función de respuesta (Yr) de un factor de influencia variable ( x ). El punto de ruptura se puede interpretar como un valor crítico , seguro o umbral más allá o por debajo del cual ocurren los efectos (no) deseados. El punto de ruptura puede ser importante en la toma de decisiones.
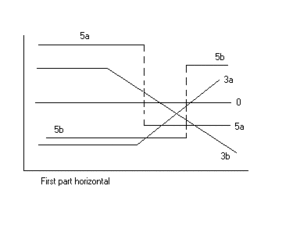
Las figuras ilustran algunos de los resultados y tipos de regresión que se pueden obtener.
Un análisis de regresión segmentada se basa en la presencia de un conjunto de ( y, x de datos), en la que y es la variable dependiente y x la variable independiente .
El método de mínimos cuadrados se aplica por separado a cada segmento, mediante el cual las dos líneas de regresión se hacen para ajustarse al conjunto de datos lo más cerca posible mientras se minimiza la suma de cuadrados de las diferencias (SSD) entre los valores observados ( y ) y calculados (Yr). de la variable dependiente, da como resultado las dos ecuaciones siguientes:
- Año = A 1 . x + K 1 para x <BP (punto de interrupción)
- Año = A 2 . x + K 2 para x > BP (punto de interrupción)
dónde:
- Yr es el valor esperado (predicho) de y para un cierto valor de x ;
- A 1 y A 2 son coeficientes de regresión (que indican la pendiente de los segmentos de línea);
- K 1 y K 2 son constantes de regresión (que indican la intersección en el eje y ).
Los datos pueden mostrar muchos tipos o tendencias, consulte las cifras.
El método también produce dos coeficientes de correlación (R):
- para x <BP (punto de interrupción)
y
- para x > BP (punto de interrupción)
dónde:
- es el SSD minimizado por segmento
y
- Y a1 e Y a2 son los valores promedio de y en los respectivos segmentos.
En la determinación de la tendencia más adecuada, se deben realizar pruebas estadísticas para asegurar que esta tendencia es confiable (significativa).
Cuando no se puede detectar un punto de ruptura significativo, se debe recurrir a una regresión sin punto de ruptura.
Ejemplo
Para la figura azul a la derecha que da la relación entre el rendimiento de mostaza (Yr = Ym, t / ha) y la salinidad del suelo ( x = Ss, expresada como conductividad eléctrica de la solución del suelo EC en dS / m) se encuentra que :
BP = 4.93, A 1 = 0, K 1 = 1.74, A 2 = −0.129, K 2 = 2.38, R 1 2 = 0.0035 (insignificante), R 2 2 = 0.395 (significativo) y:
- Ym = 1,74 t / ha para Ss <4,93 (punto de corte)
- Ym = −0,129 Ss + 2,38 t / ha para Ss> 4,93 (punto de corte)
lo que indica que las salinidades del suelo <4,93 dS / m son seguras y las salinidades del suelo> 4,93 dS / m reducen el rendimiento a 0,129 t / ha por unidad de aumento de la salinidad del suelo.
La figura también muestra los intervalos de confianza y la incertidumbre como se detalla a continuación.
Procedimientos de prueba
Las siguientes pruebas estadísticas se utilizan para determinar el tipo de tendencia:
- significancia del punto de corte (BP) expresando BP como una función de los coeficientes de regresión A 1 y A 2 y las medias Y 1 e Y 2 de los datos y y las medias X 1 y X 2 de los datos x (izquierda y derecha de BP), usando las leyes de propagación de errores en sumas y multiplicaciones para calcular el error estándar (SE) de BP, y aplicando la prueba t de Student
- significancia de A 1 y A 2 aplicando la distribución t de Student y el error estándar SE de A 1 y A 2
- significancia de la diferencia de A 1 y A 2 aplicando la distribución t de Student usando el EE de su diferencia.
- significancia de la diferencia de Y 1 e Y 2 aplicando la distribución t de Student usando el EE de su diferencia.
- Un enfoque estadístico más formal para probar la existencia de un punto de ruptura es a través de la prueba de pseudo puntuación, que no requiere la estimación de la línea segmentada.
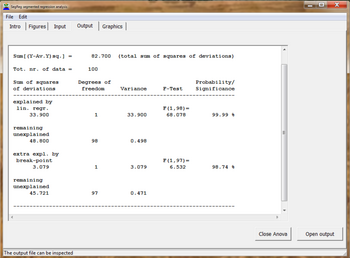
Además, se utiliza el coeficiente de correlación de todos los datos (Ra), el coeficiente de determinación o coeficiente de explicación, los intervalos de confianza de las funciones de regresión y el análisis ANOVA .
El coeficiente de determinación para todos los datos (Cd), que se maximizará en las condiciones establecidas por las pruebas de significancia, se obtiene a partir de:
donde Yr es el valor esperado (predicho) de y de acuerdo con las ecuaciones de regresión anteriores y Ya es el promedio de todos los valores de y .
El coeficiente de Cd varía entre 0 (sin explicación alguna) y 1 (explicación completa, coincidencia perfecta).
En una regresión lineal pura, no segmentada, los valores de Cd y Ra 2 son iguales. En una regresión segmentada, Cd debe ser significativamente mayor que Ra 2 para justificar la segmentación.
El valor óptimo del punto de ruptura se puede encontrar de manera que el coeficiente de Cd sea máximo .
Rango sin efecto
La regresión segmentada se usa a menudo para detectar en qué rango una variable explicativa (X) no tiene efecto sobre la variable dependiente (Y), mientras que más allá del alcance hay una respuesta clara, ya sea positiva o negativa. El alcance sin efecto puede encontrarse en la parte inicial del dominio X o, a la inversa, en su última parte. Para el análisis "sin efecto", la aplicación del método de mínimos cuadrados para el análisis de regresión segmentado puede no ser la técnica más apropiada porque el objetivo es más bien encontrar el tramo más largo sobre el cual se puede considerar que la relación YX posee pendiente cero mientras está más allá el alcance de la pendiente es significativamente diferente de cero, pero el conocimiento sobre el mejor valor de esta pendiente no es material. El método para encontrar el rango sin efecto es la regresión parcial progresiva sobre el rango, extendiendo el rango con pequeños pasos hasta que el coeficiente de regresión se vuelve significativamente diferente de cero.
En la siguiente figura, el punto de ruptura se encuentra en X = 7,9 mientras que para los mismos datos (ver figura azul arriba para el rendimiento de mostaza), el método de mínimos cuadrados produce un punto de ruptura solo en X = 4,9. El último valor es menor, pero el ajuste de los datos más allá del punto de interrupción es mejor. Por lo tanto, dependerá del propósito del análisis qué método debe emplearse.
Ver también
- Prueba de comida
- Regresión simple
- Regresión lineal
- Mínimos cuadrados ordinarios
- Splines de regresión adaptativa multivariante
- Regresión local
- Diseño de regresión discontinua
- Regresión escalonada
- SegReg (software) para regresión segmentada
Referencias
- ^ Análisis de frecuencia y regresión . Capítulo 6 en: HPRitzema (ed., 1994), Drainage Principles and Applications , Publ. 16, págs. 175-224, Instituto Internacional para la Recuperación y Mejoramiento de Tierras (ILRI), Wageningen, Países Bajos. ISBN 90-70754-33-9 . Descarga gratuita desde la página web [1] , bajo nr. 20, o directamente como PDF: [2]
- ^ Investigación de drenaje en campos de agricultores: análisis de datos . Parte del proyecto "Oro líquido" del Instituto Internacional para la Recuperación y Mejoramiento de Tierras (ILRI), Wageningen, Países Bajos. Descargar como PDF: [3]
- ^ RJOosterbaan, DPSharma, KNSingh y KVGKRao, 1990, Producción de cultivos y salinidad del suelo: evaluación de datos de campo de la India mediante regresión lineal segmentada . En: Actas del Simposio sobre drenaje de tierras para el control de la salinidad en regiones áridas y semiáridas, 25 de febrero al 2 de marzo de 1990, El Cairo, Egipto, vol. 3, Sesión V, pág. 373 - 383.
- ^ Muggeo, VMR (2016). "Prueba con un parámetro de molestia presente solo bajo la alternativa: un enfoque basado en puntaje con aplicación al modelado segmentado" (PDF) . Revista de Computación y Simulación Estadística . 86 (15): 3059-3067. doi : 10.1080 / 00949655.2016.1149855 .
- ^ La significación estadística de regresión lineal segmentada con punto de rotura utilizando el análisis de varianza y pruebas F . Descargue desde [4] bajo el nr. 13, o directamente como PDF: [5]
- ^ Análisis de regresión segmentado, Instituto Internacional de Mejora y Recuperación de Tierras (ILRI), Wageningen, Países Bajos. Descarga gratuita desde la página web [6]
- ^ Análisis de regresión parcial, Instituto internacional para la recuperación y mejora de tierras (ILRI), Wageningen, Países Bajos. Descarga gratuita desde la página web [7]