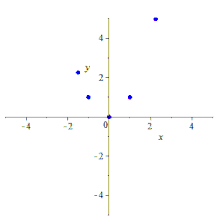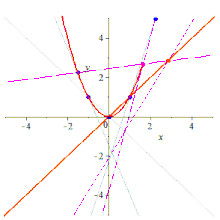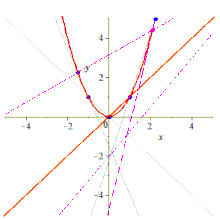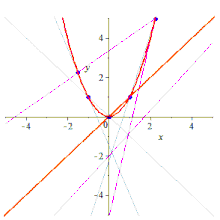
Cinco puntos determinan una cónica: Five points determine a conic

En euclidiana y proyectiva geometría , al igual que dos (distintos) puntos determinan una línea (una curva plana grado-1), cinco puntos determinan una cónica (una curva plana grado-2). Hay sutilezas adicionales para las cónicas que no existen para las líneas y, por lo tanto, la declaración y su prueba para las cónicas son más técnicas que para las líneas.

Formalmente, dados cualesquiera cinco puntos en el plano en posición lineal general , lo que significa que no hay tres colineales , hay una cónica única que pasa a través de ellos, que no será degenerada; esto es cierto tanto en el plano euclidiano como en cualquier plano proyectivo papiano . De hecho, dados cualesquiera cinco puntos hay una cónica que los atraviesa, pero si tres de los puntos son colineales, la cónica estará degenerada (reducible, porque contiene una línea) y puede que no sea única; ver discusión adicional .

Pruebas

Este resultado se puede probar de muchas formas diferentes; el argumento del recuento de dimensiones es el más directo y se generaliza en mayor grado, mientras que otras pruebas son especiales para las cónicas.

Recuento de dimensiones

Intuitivamente, pasar por cinco puntos en la posición lineal general especifica cinco restricciones lineales independientes en el espacio lineal (proyectivo) de las cónicas y, por lo tanto, especifica una cónica única, aunque esta breve declaración ignora las sutilezas.

Más precisamente, esto se ve de la siguiente manera:

• las cónicas corresponden a puntos en el espacio proyectivo de cinco dimensiones ${\ Displaystyle \ mathbf {P} ^ {5};}$
• requerir que una cónica pase a través de un punto impone una condición lineal en las coordenadas: para un fijo, la ecuación es una ecuación lineal en${\ Displaystyle (x, y),}$${\ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0}$${\ Displaystyle (A, B, C, D, E, F);}$
• mediante el recuento de dimensiones , se necesitan cinco restricciones (que la curva pase por cinco puntos) para especificar una cónica, ya que cada restricción corta la dimensión de posibilidades en 1 y una comienza con 5 dimensiones;
• en 5 dimensiones, la intersección de 5 hiperplanos (independientes) es un solo punto (formalmente, según el teorema de Bézout );
• la posición lineal general de los puntos significa que las restricciones son independientes y , por lo tanto, especifican una cónica única;
• la cónica resultante no está degenerada porque es una curva (ya que tiene más de 1 punto) y no contiene una línea (de lo contrario, se dividiría en dos líneas, al menos una de las cuales debe contener 3 de los 5 puntos, por el principio de casillero ), por lo que es irreductible.

Las dos sutilezas del análisis anterior son que el punto resultante es una ecuación cuadrática (no una ecuación lineal) y que las restricciones son independientes. La primera es simple: si A , B y C desaparecen, entonces la ecuación define una línea, y 3 puntos cualesquiera en esta (de hecho, cualquier número de puntos) se encuentran en una línea; por lo tanto, la posición lineal general garantiza una cónica. El segundo, que las restricciones son independientes, es significativamente más sutil: corresponde al hecho de que dados cinco puntos en posición lineal general en el plano, sus imágenes debajo del mapa de Veronese están en posición lineal general, lo cual es cierto porque el mapa de Veronese es birregular : es decir, si la imagen de cinco puntos satisface una relación, entonces la relación puede retirarse y los puntos originales también deben satisfacer una relación. El mapa de Veronese tiene coordenadas y el objetivo es dual al de las cónicas. El mapa de Veronese corresponde a la "evaluación de una cónica en un punto", y el enunciado sobre la independencia de las restricciones es exactamente un enunciado geométrico sobre este mapa. ${\ Displaystyle Dx + Ey + F = 0}$${\ Displaystyle \ mathbf {P} ^ {5}}$${\ Displaystyle [x ^ {2}: xy: y ^ {2}: xz: yz: z ^ {2}],}$${\ Displaystyle \ mathbf {P} ^ {5}}$${\ Displaystyle [A: B: C: D: E: F]}$ ${\ Displaystyle \ mathbf {P} ^ {5}}$

Prueba sintética

Que cinco puntos determinan una cónica se puede probar mediante geometría sintética, es decir, en términos de líneas y puntos en el plano, además de la prueba analítica (algebraica) dada anteriormente. Tal demostración se puede dar usando un teorema de Jakob Steiner , que establece:

Dada una transformación proyectiva f, entre el lápiz de líneas que pasan por un punto X y el lápiz de líneas que pasan por un punto Y, el conjunto C de puntos de intersección entre una línea x y su imagen forma una cónica. ${\ Displaystyle f (x)}$

Tenga en cuenta que X e Y están en esta cónica considerando la preimagen y la imagen de la línea XY (que es respectivamente una línea que pasa por X y una línea que pasa por Y ).

Esto se puede demostrar llevando los puntos X e Y a los puntos estándar y mediante una transformación proyectiva, en cuyo caso los lápices de líneas corresponden a las líneas horizontales y verticales en el plano, y las intersecciones de las líneas correspondientes a la gráfica de un función, que (debe mostrarse) es una hipérbola, por lo tanto, una cónica, por lo tanto, la curva original C es una cónica. ${\ displaystyle [1: 0: 0]}$${\ Displaystyle [0: 1: 0]}$

Ahora, dados cinco puntos X, Y, A, B, C, las tres líneas se pueden llevar a las tres líneas mediante una transformación proyectiva única, ya que las transformadas proyectivas son simplemente 3-transitivas en las líneas (son simplemente 3-transitivas en los puntos, por tanto, por dualidad proyectiva son 3-transitivas en líneas). Bajo este mapa, X se asigna a Y, ya que estos son los puntos de intersección únicos de estas líneas y, por lo tanto, satisfacen la hipótesis del teorema de Steiner. Por tanto, la cónica resultante contiene los cinco puntos y es la única cónica que se desee. ${\ Displaystyle XA, XB, XC}$${\ Displaystyle YA, YB, YC}$

Construcción de parábola, dados cinco puntos

Construcción

Dados cinco puntos, se puede construir la cónica que los contiene de varias formas.

Analíticamente, dadas las coordenadas de los cinco puntos, la ecuación para la cónica se puede encontrar por álgebra lineal , escribiendo y resolviendo las cinco ecuaciones en los coeficientes, sustituyendo las variables con los valores de las coordenadas: cinco ecuaciones, seis incógnitas, pero homogéneo por lo que la escala elimina una dimensión; concretamente, establecer uno de los coeficientes en 1 logra esto. ${\ Displaystyle (x_ {i}, y_ {i}) _ {i = 1,2,3,4,5}}$

Esto se puede lograr de manera bastante directa como la siguiente ecuación determinante:

${\ Displaystyle \ det {\ begin {bmatrix} x ^ {2} & xy & y ^ {2} & x & y & 1 \\ x_ {1} ^ {2} & x_ {1} y_ {1} & y_ {1} ^ {2} & x_ { 1} & y_ {1} & 1 \\ x_ {2} ^ {2} & x_ {2} y_ {2} & y_ {2} ^ {2} & x_ {2} & y_ {2} & 1 \\ x_ {3} ^ { 2} & x_ {3} y_ {3} & y_ {3} ^ {2} & x_ {3} & y_ {3} & 1 \\ x_ {4} ^ {2} & x_ {4} y_ {4} & y_ {4} ^ {2} & x_ {4} & y_ {4} & 1 \\ x_ {5} ^ {2} & x_ {5} y_ {5} & y_ {5} ^ {2} & x_ {5} & y_ {5} & 1 \ end { bmatrix}} = 0}$

Esta matriz tiene variables en su primera fila y números en todas las demás filas, por lo que el determinante es visiblemente una combinación lineal de los seis monomios de grado como máximo 2. Además, el polinomio resultante desaparece claramente en los cinco puntos de entrada (cuando ), como la matriz tiene entonces una fila repetida. ${\ Displaystyle (x, y) = (x_ {i}, y_ {i})}$

Sintéticamente, la cónica se puede construir mediante la construcción de Braikenridge-Maclaurin , aplicando el teorema de Braikenridge-Maclaurin , que es el inverso del teorema de Pascal . El teorema de Pascal establece que dados 6 puntos en una cónica (un hexágono), las líneas definidas por lados opuestos se cruzan en tres puntos colineales. Esto se puede revertir para construir las posibles ubicaciones para un sexto punto, dados los 5 existentes.

Generalizaciones

La generalización natural es preguntar qué valor de k una configuración de k puntos (en posición general) en n -espacio determina una variedad de grado d y dimensión m , que es una cuestión fundamental en geometría enumerativa .

Un caso simple de esto es para una hipersuperficie (una subvariedad de codimensión 1, los ceros de un solo polinomio, el caso ), de la cual las curvas planas son un ejemplo. ${\ Displaystyle m = n-1}$

En el caso de una hipersuperficie, la respuesta se da en términos del coeficiente multiset , más familiarmente el coeficiente binomial , o más elegantemente el factorial ascendente , como:

${\ Displaystyle k = \ left (\! \! {n + 1 \ elige d} \! \! \ right) -1 = {n + d \ elige d} -1 = {\ frac {1} {n! }} (d + 1) ^ {(n)} - 1.}$

Esto es a través del análisis análogo del mapa de Veronese : k puntos en posición general imponen k condiciones lineales independientes en una variedad (porque el mapa de Veronese es birregular), y el número de monomios de grado d en variables (el espacio proyectivo n- dimensional tiene coordenadas homogéneas) es de la que se resta 1 debido a la proyectivización: multiplicar un polinomio por una constante no cambia sus ceros. ${\ Displaystyle n + 1}$${\ Displaystyle n + 1}$${\ Displaystyle \ textstyle {\ left (\! \! {n + 1 \ elige d} \! \! \ right)},}$

En la fórmula anterior, el número de puntos k es un polinomio en d de grado n, con coeficiente principal${\ Displaystyle 1 / n!}$

En el caso de curvas planas, donde la fórmula se convierte en: ${\ Displaystyle n = 2,}$

${\ Displaystyle \ textstyle {\ frac {1} {2}} (d + 1) (d + 2) -1 = \ textstyle {\ frac {1} {2}} (d ^ {2} + 3d)}$

cuyos valores para son - no hay curvas de grado 0 (un solo punto es un punto y, por lo tanto, está determinado por un punto, que es la codimensión 2), 2 puntos determinan una línea, 5 puntos determinan una cónica, 9 puntos determinan una cúbica , 14 puntos determinan un cuartico, y así sucesivamente. ${\ Displaystyle d = 0,1,2,3,4}$${\ Displaystyle 0,2,5,9,14}$

Resultados relacionados

Mientras que cinco puntos determinan una cónica, los conjuntos de seis o más puntos en una cónica no están en posición general, es decir, están restringidos como se demuestra en el teorema de Pascal .

De manera similar, aunque nueve puntos determinan un cúbico, si los nueve puntos se encuentran en más de un cúbico, es decir, son la intersección de dos cúbicos, entonces no están en posición general y, de hecho, satisfacen una restricción de adición, como se indica en el Cayley. –Teorema de Bacharach .

Cuatro puntos no determinan una cónica, sino más bien un lápiz , el sistema lineal unidimensional de cónicas que pasan todas por los cuatro puntos (formalmente, tienen los cuatro puntos como lugar de base ). De manera similar, tres puntos determinan un sistema lineal de 2 dimensiones (neto), dos puntos determinan un sistema lineal de 3 dimensiones (red), un punto determina un sistema lineal de 4 dimensiones y los puntos cero no imponen restricciones sobre el sistema lineal de 5 dimensiones. sistema de todas las cónicas.

Los círculos apolíneos son dos familias de 1 parámetro determinadas por 2 puntos.

Como es bien sabido, tres puntos no colineales determinan un círculo en la geometría euclidiana y dos puntos distintos determinan un lápiz de círculos como los círculos apolíneos . Estos resultados parecen ir en contra del resultado general, ya que los círculos son casos especiales de cónicas. Sin embargo, en un plano proyectivo papiano , una cónica es un círculo solo si pasa por dos puntos específicos en la línea en el infinito , por lo que un círculo está determinado por cinco puntos no colineales, tres en el plano afín y estos dos puntos especiales. Consideraciones similares explican el número de puntos más pequeño de lo esperado que se necesitan para definir lápices de círculos.

Tangencia

En lugar de pasar por puntos, una condición diferente en una curva es ser tangente a una línea determinada. Ser tangente a cinco líneas dadas también determina una cónica, por dualidad proyectiva , pero desde el punto de vista algebraico, la tangencia a una línea es una restricción cuadrática , por lo que el conteo de dimensiones ingenuo produce 2 ⁵  = 32 cónicas tangentes a cinco líneas dadas, de las cuales 31 debe atribuirse a cónicas degeneradas, como se describe en los factores fudge en geometría enumerativa ; Formalizar esta intuición requiere un desarrollo adicional significativo para justificarlo.

Otro problema clásico en geometría enumerativa, de similar antigüedad a las cónicas, es el Problema de Apolonio : un círculo que es tangente a tres círculos en general determina ocho círculos, ya que cada uno de ellos es una condición cuadrática y 2 ³  = 8. Como pregunta en geometría real, un análisis completo involucra muchos casos especiales, y el número real de círculos puede ser cualquier número entre 0 y 8, excepto 7.

Ver también

• Teorema de Cramer (curvas algebraicas) , para una generalización a curvas planas de n -ésimo grado

Referencias

enlaces externos

• Cinco puntos determinan una sección cónica , demostración interactiva de Wolfram