Esfenocorona aumentada - Augmented sphenocorona

Esfenocorona aumentada
Escribe	Johnson J 86 - J 87 - J 88
Caras	4 + 6x2 triángulos 1 cuadrado
Bordes	26
Vértices	11
Configuración de vértice	1 (3 4 ) 2 (3 3 .4) 3x2 (3 5 ) 2 (3 4 .4)
Grupo de simetría	C s
Poliedro doble	-
Propiedades	convexo
Neto

Modelo 3D de una esfenocorona aumentada

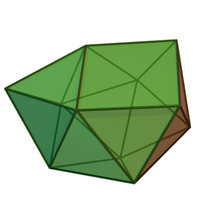
En geometría , la esfenocorona aumentada es uno de los sólidos de Johnson ( J ₈₇ ), y se obtiene agregando una pirámide cuadrada a una de las caras cuadradas de la esfenocorona . Es el único sólido de Johnson que surge de manipulaciones de "cortar y pegar" donde los componentes no son todos prismas, antiprismas o secciones de sólidos platónicos o de Arquímedes .

Un sólido de Johnson es uno de los 92 poliedros estrictamente convexos que se componen de caras poligonales regulares pero que no son poliedros uniformes (es decir, no son sólidos platónicos , sólidos de Arquímedes , prismas o antiprismas ). Fueron nombrados por Norman Johnson , quien primero enumeró estos poliedros en 1966.

Johnson usa el prefijo esfeno- para referirse a un complejo en forma de cuña formado por dos lunas adyacentes , una luna es un cuadrado con triángulos equiláteros unidos en lados opuestos. Asimismo, el sufijo -corona se refiere a un complejo en forma de corona de 8 triángulos equiláteros. Finalmente, el descriptor aumentado implica que se adjunta otro poliedro, en este caso una pirámide . La unión de ambos complejos junto con la pirámide da como resultado la esfenocorona aumentada.

Coordenadas cartesianas

Para calcular las coordenadas cartesianas de la esfenocorona aumentada, se puede comenzar calculando las coordenadas de la esfenocorona. Sea k ≈ 0.85273 la raíz positiva más pequeña del polinomio cuártico

${\ Displaystyle 60x ^ {4} -48x ^ {3} -100x ^ {2} + 56x + 23.}$

Entonces, las coordenadas cartesianas de una esfenocorona con longitud de borde 2 están dadas por la unión de las órbitas de los puntos

${\ Displaystyle \ left (0,1,2 {\ sqrt {1-k ^ {2}}} \ right), \, (2k, 1,0), \ left (0,1 + {\ frac {\ sqrt {3-4k ^ {2}}} {\ sqrt {1-k ^ {2}}}}, {\ frac {1-2k ^ {2}} {\ sqrt {1-k ^ {2}} }} \ derecha), \, \ izquierda (1,0, - {\ sqrt {2 + 4k-4k ^ {2}}} \ derecha)}$

bajo la acción del grupo generado por reflexiones sobre el plano xz y el plano yz. Al calcular el centroide y el vector unitario normal de una de las caras cuadradas se obtiene la ubicación de su último vértice como

${\ Displaystyle \ left (k + {\ sqrt {2-2k ^ {2}}}, 0, k + {\ sqrt {2-2k ^ {2}}} \ right).}$

A continuación, se puede calcular el área de la superficie de un cuadrado chato de longitud de borde a como

${\ Displaystyle A = \ left (1 + 4 {\ sqrt {3}} \ right) a ^ {2} \ approx 7,92820a ^ {2},}$

y su volumen como

${\ Displaystyle V = \ left ({\ frac {1} {2}} {\ sqrt {1 + 3 {\ sqrt {\ frac {3} {2}}} + {\ sqrt {13 + 3 {\ sqrt {6}}}}}} + {\ frac {1} {3 {\ sqrt {2}}}} \ right) a ^ {3} \ approx 1.75105a ^ {3}.}$

Referencias

enlaces externos

• Eric W. Weisstein , esfenocorona aumentada ( sólido de Johnson ) en MathWorld .

Este artículo relacionado con el poliedro es un trozo . Puedes ayudar a Wikipedia expandiéndolo .

• v
• t
• mi