Teorema de Seifert-Van Kampen - Seifert–Van Kampen theorem

En matemáticas , el teorema de topología algebraica de Seifert-Van Kampen (llamado así por Herbert Seifert y Egbert van Kampen ), a veces llamado simplemente teorema de Van Kampen , expresa la estructura del grupo fundamental de un espacio topológico en términos de los grupos fundamentales de dos , subespacios conectados por caminos que cubren . Por lo tanto, se puede utilizar para cálculos del grupo fundamental de espacios que se construyen a partir de otros más simples. ${\ Displaystyle X}$${\ Displaystyle X}$

Teorema de Van Kampen para grupos fundamentales

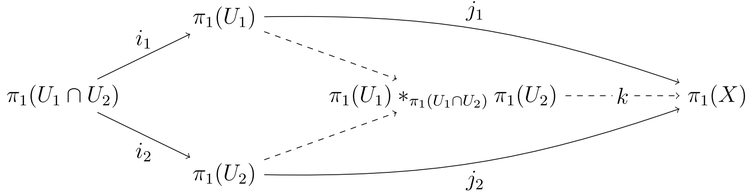
Sea X un espacio topológico que es la unión de dos subespacios abiertos y conectados por caminos U ₁ , U ₂ . Suponga que U ₁ ∩ U ₂ está conectado a una ruta y no está vacío, y sea x ₀ un punto en U ₁ ∩ U ₂ que se usará como la base de todos los grupos fundamentales. Los mapas de inclusión de U ₁ y U ₂ en X inducen homomorfismos de grupo y . Entonces X está conectado con la ruta y forma un diagrama de expulsión conmutativa : ${\ Displaystyle j_ {1}: \ pi _ {1} (U_ {1}, x_ {0}) \ to \ pi _ {1} (X, x_ {0})}$${\ Displaystyle j_ {2}: \ pi _ {1} (U_ {2}, x_ {0}) \ to \ pi _ {1} (X, x_ {0})}$${\ Displaystyle j_ {1}}$${\ Displaystyle j_ {2}}$

El morfismo natural k es un isomorfismo. Es decir, el grupo fundamental de X es el producto libre de los grupos fundamentales de U ₁ y U ₂ con la fusión de . ${\ Displaystyle \ pi _ {1} (U_ {1} \ cap U_ {2}, x_ {0})}$

Por lo general, los morfismos inducidos por la inclusión en este teorema no son en sí mismos inyectivos, y la versión más precisa del enunciado es en términos de expulsiones de grupos.

Teorema de Van Kampen para grupos fundamentales

Desafortunadamente, el teorema dado anteriormente no calcula el grupo fundamental del círculo, que es el ejemplo básico más importante en topología algebraica. La razón es que el círculo no se puede realizar como la unión de dos conjuntos abiertos con intersección conectada. Este problema se puede resolver trabajando con el grupoide fundamental en un conjunto A de puntos base, elegidos de acuerdo con la geometría de la situación. Por tanto, para el círculo, se utilizan dos puntos de base. ${\ Displaystyle \ pi _ {1} (X, A)}$

Este groupoid consiste en clases de homotopía relativos a los puntos finales de caminos en X que une los puntos de A ∩ X . En particular, si X es un espacio contráctil, y A consta de dos puntos distintos de X , entonces se ve fácilmente que es isomorfo al grupoide que a menudo se escribe con dos vértices y exactamente un morfismo entre dos vértices cualesquiera. Este grupoide juega un papel en la teoría de grupos análogos al del grupo de enteros en la teoría de grupos. El groupoid también permite a los groupoids una noción de homotopía: es un objeto de intervalo unitario en la categoría de groupoids. ${\ Displaystyle \ pi _ {1} (X, A)}$${\ Displaystyle {\ mathcal {I}}}$${\ Displaystyle {\ mathcal {I}}}$

Una unión conectada de dos espacios no conectados, con un conjunto de puntos base.

La categoría de grupoides admite todos los colimits y, en particular, todos los pushouts.

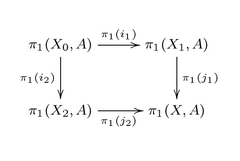
Teorema. Deje que el espacio topológico X esté cubierto por los interiores de dos subespacios X ₁ , X ₂ y sea A un conjunto que se encuentra con cada componente de trayectoria de X ₁ , X ₂ y X ₀ = X ₁ ∩ X ₂ . Entonces A se encuentra con cada componente de la trayectoria de X y el diagrama P de morfismos inducidos por inclusión

es un diagrama pushout en la categoría de grupoides.

Este teorema da la transición de la topología al álgebra, al determinar completamente el grupoide fundamental ; entonces uno tiene que usar álgebra y combinatoria para determinar un grupo fundamental en algún punto base. ${\ Displaystyle \ pi _ {1} (X, A)}$

Una interpretación del teorema es que calcula los tipos 1 de homotopía. Para ver su utilidad, se pueden encontrar fácilmente casos en los que X está conectado pero es la unión de los interiores de dos subespacios, cada uno con, por ejemplo, 402 componentes de trayectoria y cuya intersección tiene, por ejemplo, 1004 componentes de trayectoria. La interpretación de este teorema como una herramienta de cálculo para "grupos fundamentales" necesita cierto desarrollo de la "teoría combinatoria grupoide". Este teorema implica el cálculo del grupo fundamental del círculo como grupo de enteros, ya que el grupo de enteros se obtiene del grupoide identificando, en la categoría de grupoides, sus dos vértices. ${\ Displaystyle {\ mathcal {I}}}$

Existe una versión del último teorema cuando X está cubierto por la unión de los interiores de una familia de subconjuntos. ${\ Displaystyle \ {U _ {\ lambda}: \ lambda \ in \ Lambda \}}$

La conclusión es que si A se encuentra con cada componente de la ruta de todas las intersecciones de 1,2,3 veces de los conjuntos , entonces A se encuentra con todas las componentes de la ruta de X y el diagrama ${\ Displaystyle U _ {\ lambda}}$

${\ Displaystyle \ bigsqcup _ {(\ lambda, \ mu) \ in \ Lambda ^ {2}} \ pi _ {1} (U _ {\ lambda} \ cap U _ {\ mu}, A) \ rightrightarrows \ bigsqcup _ {\ lambda \ in \ Lambda} \ pi _ {1} (U _ {\ lambda}, A) \ rightarrow \ pi _ {1} (X, A)}$

de morfismos inducidos por inclusiones es un coequalizador en la categoría de los grupoides.

[...] la gente todavía persiste obstinadamente, al calcular con grupos fundamentales, en fijar un único punto base, en lugar de elegir hábilmente todo un paquete de puntos que es invariable bajo las simetrías de la situación, que así se pierden en el camino. En determinadas situaciones (como los teoremas de descendencia para grupos fundamentales a la de Van Kampen) es mucho más elegante, incluso indispensable para comprender algo, trabajar con agrupaciones fundamentales con respecto a un paquete adecuado de puntos base [...]

-  Alexander Grothendieck , Esquisse d'un Program (Sección 2, traducción al inglés )

Formulaciones equivalentes

En el lenguaje de la teoría combinatoria de grupos , si es un espacio topológico; y son subespacios abiertos, conectados por caminos de ; no está vacío y conectado a un camino; y ; luego es el producto libre con amalgama de y , con respecto a los homomorfismos (no necesariamente inyectivos) y . Presentaciones grupales dadas : ${\ Displaystyle X}$${\ Displaystyle U}$${\ Displaystyle V}$${\ Displaystyle X}$${\ Displaystyle U \ cap V}$${\ Displaystyle w \ in U \ cap V}$${\ Displaystyle \ pi _ {1} (X, w)}$${\ Displaystyle \ pi _ {1} (U, w)}$${\ Displaystyle \ pi _ {1} (V, w)}$${\ Displaystyle I: \ pi _ {1} (U \ cap V, w) \ to \ pi _ {1} (U, w)}$${\ Displaystyle J: \ pi _ {1} (U \ cap V, w) \ to \ pi _ {1} (V, w)}$

${\ Displaystyle {\ begin {alineado} \ pi _ {1} (U, w) & = \ langle u_ {1}, \ cdots, u_ {k} \ mid \ alpha _ {1}, \ cdots, \ alpha _ {l} \ rangle \\\ pi _ {1} (V, w) & = \ langle v_ {1}, \ cdots, v_ {m} \ mid \ beta _ {1}, \ cdots, \ beta _ {n} \ rangle \\\ pi _ {1} (U \ cap V, w) & = \ langle w_ {1}, \ cdots, w_ {p} \ mid \ gamma _ {1}, \ cdots, \ gamma _ {q} \ rangle \ end {alineado}}}$

la fusión se puede presentar como

${\ Displaystyle \ pi _ {1} (X, w) = \ left \ langle u_ {1}, \ cdots, u_ {k}, v_ {1}, \ cdots, v_ {m} \ left | \ alpha _ {1}, \ cdots, \ alpha _ {l}, \ beta _ {1}, \ cdots, \ beta _ {n}, I (w_ {1}) J (w_ {1}) ^ {- 1} , \ cdots, I (w_ {p}) J (w_ {p}) ^ {- 1} \ right. \ right \ rangle.}$

En la teoría de categorías , es la expulsión , en la categoría de grupos, del diagrama: ${\ Displaystyle \ pi _ {1} (X, w)}$

${\ Displaystyle \ pi _ {1} (U, w) \ gets \ pi _ {1} (U \ cap V, w) \ to \ pi _ {1} (V, w).}$

Ejemplos de

2 esferas

Se puede usar el teorema de Van Kampen para calcular grupos fundamentales para espacios topológicos que se pueden descomponer en espacios más simples. Por ejemplo, considere la esfera . Recoger conjuntos abiertos y donde n y s denotan los postes del norte y respectivamente. Entonces tenemos la propiedad de que A , B y A ∩ B son conjuntos conectados de camino abierto. Así podemos ver que hay un diagrama conmutativo que incluye A ∩ B en A y B y luego otra inclusión de A y B en y que hay un diagrama correspondiente de homomorfismos entre los grupos fundamentales de cada subespacio. La aplicación del teorema de Van Kampen da el resultado ${\ Displaystyle S ^ {2}}$${\ Displaystyle A = S ^ {2} \ setminus \ {n \}}$${\ Displaystyle B = S ^ {2} \ setminus \ {s \}}$${\ Displaystyle S ^ {2}}$

${\ Displaystyle \ pi _ {1} (S ^ {2}) = \ pi _ {1} (A) \ cdot \ pi _ {1} (B) / \ ker (\ Phi).}$

Sin embargo, A y B son ambos homeomorfo a R ² que está conectado simplemente, por lo tanto A y B tienen grupos fundamentales triviales. De esto se desprende claramente que el grupo fundamental de es trivial. ${\ Displaystyle S ^ {2}}$

Suma de espacios en cuña

Dados dos espacios en punta y podemos formar su suma de cuña , , tomando el cociente de mediante la identificación de sus dos puntos de base. ${\ Displaystyle (X, x)}$${\ Displaystyle (Y, y)}$${\ Displaystyle (X \ vee Y, p)}$${\ Displaystyle X \ coprod Y}$

Si admite una vecindad abierta contráctil y admite una vecindad abierta contráctil (que es el caso si, por ejemplo, y son complejos CW ), entonces podemos aplicar el teorema de Van Kampen tomando y como los dos conjuntos abiertos y concluimos que el El grupo fundamental de la cuña es el producto libre de los grupos fundamentales de los dos espacios con los que partimos: ${\ Displaystyle x}$${\ Displaystyle U \ subconjunto X}$${\ Displaystyle y}$${\ Displaystyle V \ subconjunto Y}$${\ Displaystyle X}$${\ Displaystyle Y}$${\ Displaystyle X \ vee Y}$${\ Displaystyle X \ vee V}$${\ displaystyle U \ vee Y}$

${\ Displaystyle \ pi _ {1} (X \ vee Y, p) \ cong \ pi _ {1} (X, x) * \ pi _ {1} (Y, y)}$.

Superficies orientables del género g

Un ejemplo más complicado es el cálculo del grupo fundamental de una superficie orientable del género n S , también conocido como el grupo de superficie del género n . Se puede construir S usando su polígono fundamental estándar . Para el primer conjunto abierto A , elija un disco dentro del centro del polígono. Escoja B a ser el complemento en S del punto central de A . Entonces, la intersección de A y B es un anillo, que se sabe que es homotopía equivalente a (y por lo tanto tiene el mismo grupo fundamental que) un círculo. Entonces , que son los enteros y . Por lo tanto, la inclusión de en envía cualquier generador al elemento trivial. Sin embargo, la inclusión de into no es trivial. Para entender esto, primero hay que calcular . Esto se hace fácilmente ya que se puede retraer la deformación B (que es S con un punto eliminado) en los bordes etiquetados por ${\ Displaystyle \ pi _ {1} (A \ cap B) = \ pi _ {1} (S ^ {1})}$${\ Displaystyle \ pi _ {1} (A) = \ pi _ {1} (D ^ {2}) = {1}}$${\ Displaystyle \ pi _ {1} (A \ cap B)}$${\ Displaystyle \ pi _ {1} (A)}$${\ Displaystyle \ pi _ {1} (A \ cap B)}$${\ Displaystyle \ pi _ {1} (B)}$${\ Displaystyle \ pi _ {1} (B)}$

${\ Displaystyle A_ {1} B_ {1} A_ {1} ^ {- 1} B_ {1} ^ {- 1} A_ {2} B_ {2} A_ {2} ^ {- 1} B_ {2} ^ {- 1} \ cdots A_ {n} B_ {n} A_ {n} ^ {- 1} B_ {n} ^ {- 1}.}$

Se sabe que este espacio es la suma en cuña de 2 n círculos (también llamado ramo de círculos ), que además se sabe que tiene un grupo fundamental isomorfo al grupo libre con 2 n generadores, que en este caso se puede representar por los bordes a sí mismos: . Ahora tenemos suficiente información para aplicar el teorema de Van Kampen. Los generadores son los bucles ( A simplemente está conectado, por lo que no aporta generadores) y hay exactamente una relación: ${\ Displaystyle \ {A_ {1}, B_ {1}, \ cdots, A_ {n}, B_ {n} \}}$${\ Displaystyle \ {A_ {1}, B_ {1}, \ cdots, A_ {n}, B_ {n} \}}$

${\ Displaystyle A_ {1} B_ {1} A_ {1} ^ {- 1} B_ {1} ^ {- 1} A_ {2} B_ {2} A_ {2} ^ {- 1} B_ {2} ^ {- 1} \ cdots A_ {n} B_ {n} A_ {n} ^ {- 1} B_ {n} ^ {- 1} = 1.}$

Usando generadores y relaciones, este grupo se denota

${\ Displaystyle \ left \ langle A_ {1}, B_ {1}, \ cdots, A_ {n}, B_ {n} \ left | A_ {1} B_ {1} A_ {1} ^ {- 1} B_ {1} ^ {- 1} \ cdots A_ {n} B_ {n} A_ {n} ^ {- 1} B_ {n} ^ {- 1} \ right. \ Right \ rangle.}$

Conectividad simple

Si X es el espacio que se puede escribir como la unión de dos abiertos simplemente conectados conjuntos U y V con U ∩ V no vacío y conectado path- , entonces X está conectado simplemente.

Generalizaciones

Como se explicó anteriormente, este teorema fue extendido por Ronald Brown al caso no conectado mediante el uso del grupoide fundamental en un conjunto A de puntos base. El teorema de las cubiertas arbitrarias, con la restricción de que A se encuentra con las tres intersecciones de los conjuntos de la cubierta, se da en el artículo de Brown y Abdul Razak Salleh. El teorema y la demostración del grupo fundamental, pero utilizando algunos métodos grupales, también se dan en el libro de J. Peter May . La versión que permite más de dos conjuntos superpuestos pero con A un singleton también se da en el libro de Allen Hatcher a continuación, teorema 1.20. ${\ Displaystyle \ pi _ {1} (X, A)}$

En el libro de Ronald Brown se dan aplicaciones del grupoide fundamental en un conjunto de puntos base al teorema de la curva de Jordan , cubriendo espacios y espacios orbitales . En el caso de los espacios orbitales, conviene tomar A para incluir todos los puntos fijos de la acción. Un ejemplo aquí es la acción de conjugación en el círculo.

Las referencias a versiones de dimensiones superiores del teorema que proporcionan cierta información sobre tipos de homotopía se dan en un artículo sobre teorías de grupos de dimensiones superiores y grupoides. Así, Ronald Brown y Philip J. Higgins dieron un teorema bidimensional de Van Kampen que calcula segundos grupos de homotopía relativa no belianos. Brown, Higgins y Rafael Sivera dan una descripción completa y extensiones a todas las dimensiones, mientras que Ronald Brown y Jean-Louis Loday dan una extensión a n -cubos de espacios .

Los grupos fundamentales también aparecen en geometría algebraica y son el tema principal del primer Séminaire de géométrie algébrique (SGA1) de Alexander Grothendieck . Allí aparece una versión del teorema de Van Kampen, que se demuestra en líneas muy diferentes a las de la topología algebraica, es decir, mediante la teoría de la descendencia. Una prueba similar funciona en topología algebraica.

Ver también

• Álgebra de dimensiones superiores
• Teoría de categorías superiores
• Pseudocírculo
• Ronald Brown (matemático)

Notas

Referencias

• Allen Hatcher, topología algebraica. (2002) Cambridge University Press, Cambridge, xii + 544 págs. ISBN  0-521-79160-X e ISBN  0-521-79540-0
• Peter May, un curso conciso en topología algebraica. (1999) University of Chicago Press, ISBN  0-226-51183-9 (la sección 2.7 proporciona una presentación teórica de categorías del teorema como un colimit en la categoría de grupoides) .
• Ronald Brown, Groupoids y el teorema de Van Kampen, Proc. London Math. Soc . (3) 17 (1967) 385–401.
• Discusión de Mathoverflow en muchos puntos base
• Ronald Brown, Topología y agrupaciones (2006) Booksurge LLC ISBN  1-4196-2722-8
• R. Brown y A. Razak, Un teorema de Van Kampen para uniones de espacios no conectados, Archiv. Matemáticas. 42 (1984) 85–88. (Este artículo da probablemente la versión óptima del teorema, es decir, la versión grupoide del teorema para una cubierta abierta arbitraria y un conjunto de puntos base que cumple con cada componente de la trayectoria de cada intersección de 1-.2-3 veces de los conjuntos de la cubierta.)
• PJ Higgins, Categorías y grupos (1971) Van Nostrand Reinhold
• Ronald Brown, Teoría de grupos de dimensiones superiores (2007) (Ofrece una visión amplia de los teoremas de Van Kampen de dimensiones superiores que involucran múltiples grupoides) .
• Greenberg, Marvin J .; Harper, John R. (1981), Topología algebraica. Un primer curso , Serie de notas de conferencias de matemáticas, 58 , Benjamin / Cummings, ISBN 0805335579
• Seifert, H., Konstruction drei dimensionaler geschlossener Raume . Berichte Sachs. Akad. Leipzig, Math.-Phys. Kl. (83) (1931) 26–66.
• ER van Kampen. Sobre la conexión entre los grupos fundamentales de algunos espacios relacionados. Revista Estadounidense de Matemáticas, vol. 55 (1933), págs. 261-267.
• Brown, R., Higgins, P. J, Sobre la conexión entre los segundos grupos de homotopía relativa de algunos espacios relacionados , Proc. London Math. Soc. (3) 36 (1978) 193–212.
• Brown, R., Higgins, PJ y Sivera, R .. 2011, EMS Tracts in Mathematics Vol.15 (2011) Topología algebraica nobeliana: espacios filtrados, complejos cruzados, grupoides homotópicos cúbicos ; (La primera de las tres partes analiza las aplicaciones de las versiones de 1 y 2 dimensiones del teorema de Seifert-van Kampen. La última permite cálculos de segundos grupos de homotopía relativa no belianos y, de hecho, de 2 tipos de homotopía. La segunda parte se aplica un teorema de van Kampen de homotopía superior para complejos cruzados, demostrado en la Parte III.)
• "Resultado del teorema de Van Kampen" . PlanetMath .
• R. Brown, H. Kamps, T. Porter: Un grupo doble homotopía de un espacio de Hausdorff II: un teorema de Van Kampen ', Teoría y aplicaciones de categorías, 14 (2005) 200-220.
• Dylan GL Allegretti, Simplicial Sets y Van Kampen's Theorem (Discute versiones generalizadas del teorema de Van Kampen aplicadas a espacios topológicos y conjuntos simpliciales).
• R. Brown y J.-L. Loday, "Teoremas de Van Kampen para diagramas de espacios", Topología 26 (1987) 311–334.

Este artículo incorpora material del teorema de Van Kampen sobre PlanetMath , que tiene la licencia Creative Commons Attribution / Share-Alike License .

enlaces externos

• Medios relacionados con el teorema de Seifert-Van Kampen en Wikimedia Commons