Topología (circuitos eléctricos) - Topology (electrical circuits)
La topología de un circuito electrónico es la forma que adopta la red de interconexiones de los componentes del circuito. Los diferentes valores o clasificaciones específicos de los componentes se consideran como la misma topología. La topología no se ocupa de la disposición física de los componentes de un circuito ni de sus posiciones en un diagrama de circuito ; De manera similar al concepto matemático de topología , solo se ocupa de las conexiones que existen entre los componentes. Puede haber numerosos diseños físicos y diagramas de circuitos que equivalen a la misma topología.
Estrictamente hablando, reemplazar un componente por uno de un tipo completamente diferente sigue siendo la misma topología. En algunos contextos, sin embargo, estos pueden describirse libremente como topologías diferentes. Por ejemplo, intercambiar inductores y condensadores en un filtro de paso bajo da como resultado un filtro de paso alto. Estos pueden describirse como topologías de paso alto y paso bajo aunque la topología de la red sea idéntica. Un término más correcto para estas clases de objeto (es decir, una red donde se especifica el tipo de componente pero no el valor absoluto) es red prototipo .
La topología de redes electrónicas está relacionada con la topología matemática , en particular, para las redes que contienen solo dispositivos de dos terminales, la topología de circuitos puede verse como una aplicación de la teoría de grafos . En un análisis de red de dicho circuito desde un punto de vista topológico, los nodos de la red son los vértices de la teoría de grafos y las ramas de la red son los bordes de la teoría de grafos.
La teoría de grafos estándar se puede ampliar para tratar con componentes activos y dispositivos de terminales múltiples, como circuitos integrados . Los gráficos también se pueden utilizar en el análisis de redes infinitas .
Diagramas de circuitos
Los diagramas de circuitos de este artículo siguen las convenciones habituales en electrónica; las líneas representan conductores, los círculos pequeños rellenos representan uniones de conductores, los círculos pequeños abiertos representan terminales para la conexión al mundo exterior. En la mayoría de los casos, las impedancias se representan mediante rectángulos. Un diagrama de circuito práctico usaría los símbolos específicos para resistencias , inductores , capacitores , etc., pero la topología no se preocupa por el tipo de componente en la red, por lo que se ha usado el símbolo para una impedancia general .
La sección de teoría de grafos de este artículo ofrece un método alternativo para representar redes.
Nombres de topología
Muchos nombres de topología se relacionan con su apariencia cuando se dibujan en forma de diagrama. La mayoría de los circuitos se pueden dibujar de diversas formas y, en consecuencia, tienen una variedad de nombres. Por ejemplo, los tres circuitos que se muestran en la figura 1.1 se ven todos diferentes pero tienen topologías idénticas.
Este ejemplo también demuestra una convención común de nombrar topologías después de una letra del alfabeto con la que tienen semejanza. Las letras del alfabeto griego también se pueden usar de esta manera, por ejemplo, topología Π ( pi ) y topología Δ ( delta ).
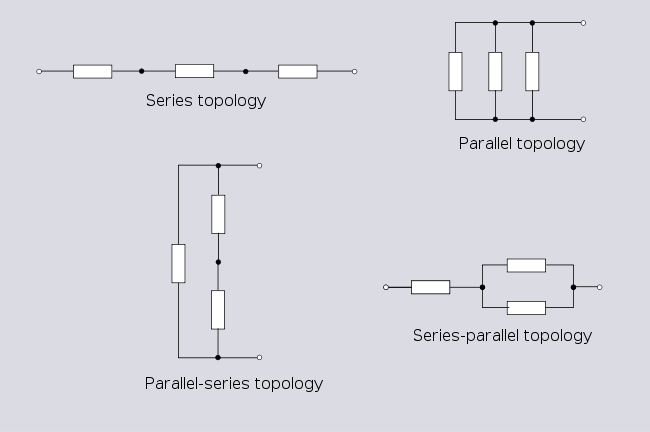
Topologías en serie y en paralelo
Para una red con dos ramas, solo hay dos topologías posibles: serie y paralelo .
Incluso para estas topologías más simples, existen variaciones en la forma en que se puede presentar el circuito.

Para una red con tres ramas, hay cuatro topologías posibles;
Tenga en cuenta que la topología de series paralelas es otra representación de la topología Delta que se analiza más adelante.
Las topologías en serie y en paralelo se pueden seguir construyendo con un número cada vez mayor de ramas hasta el infinito . El número de topologías únicas que se pueden obtener de n ramas es 2 n-1 . El número total de topologías únicas que se pueden obtener con no más de n ramas es 2 n -1.
Topologías Y y Δ
Y y Δ son topologías importantes en el análisis de redes lineales debido a que son las redes de tres terminales más simples posibles. Una transformada Y-Δ está disponible para circuitos lineales. Esta transformación es importante porque hay algunas redes que no se pueden analizar en términos de combinaciones en serie y en paralelo. Estas redes surgen a menudo en circuitos de potencia trifásicos, ya que son las dos topologías más comunes para los devanados de transformadores o motores trifásicos.
Un ejemplo de esto es la red de la figura 1.6, que consta de una red Y conectada en paralelo con una red Δ. Digamos que se desea calcular la impedancia entre dos nodos de la red. En muchas redes, esto se puede hacer mediante aplicaciones sucesivas de las reglas para la combinación de impedancias en serie o en paralelo. Sin embargo, esto no es posible en este caso donde se necesita la transformada Y-Δ además de las reglas en serie y en paralelo. La topología Y también se denomina topología en estrella. Sin embargo, la topología en estrella también puede referirse al caso más general de muchas ramas conectadas al mismo nodo en lugar de solo tres.
Topologías de filtros simples

Las topologías que se muestran en la figura 1.7 se utilizan comúnmente para diseños de filtros y atenuadores . La sección en L es una topología idéntica a la topología del divisor de potencial. La sección en T es una topología idéntica a la topología Y. La sección Π es una topología idéntica a la topología Δ.
Todas estas topologías pueden verse como una pequeña sección de una topología de escalera . Las secciones más largas normalmente se describirían como topología de escalera. Este tipo de circuitos se analizan y caracterizan comúnmente en términos de una red de dos puertos .
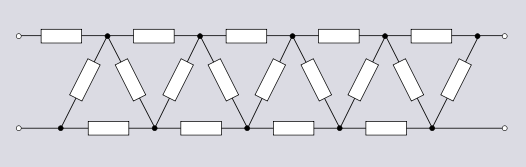
Topología de puente
La topología de puente es una topología importante con muchos usos tanto en aplicaciones lineales como no lineales, que incluyen, entre muchos otros, el puente rectificador , el puente de Wheatstone y el ecualizador de fase de celosía . Hay varias formas de representar la topología de puentes en los diagramas de circuitos. La primera representación en la figura 1.8 es la representación tradicional de un circuito de puente. La segunda representación muestra claramente la equivalencia entre la topología del puente y una topología derivada de combinaciones en serie y en paralelo. La tercera representación se conoce más comúnmente como topología de celosía. No es tan obvio que esto sea topológicamente equivalente. Se puede ver que esto es así al visualizar el nodo superior izquierdo movido a la derecha del nodo superior derecho.
Es normal llamar a una topología de puente de red solo si se utiliza como una red de dos puertos con los puertos de entrada y salida , cada uno de los cuales consta de un par de nodos diagonalmente opuestos. Se puede ver que la topología de caja en la figura 1.7 es idéntica a la topología de puente, pero en el caso del filtro, los puertos de entrada y salida son cada uno un par de nodos adyacentes . A veces, el componente de carga (o indicación nula) en el puerto de salida del puente se incluirá en la topología del puente como se muestra en la figura 1.9.
Topologías puenteadas T y Twin-T
La topología de puente en T se deriva de la topología de puente de la forma que se explica en el artículo de la red Zobel . Hay muchas topologías derivadas que también se tratan en el mismo artículo.
También existe una topología Twin-T que tiene aplicaciones prácticas en las que es deseable que la entrada y la salida compartan un terminal común ( tierra ). Esto puede deberse, por ejemplo, a que las conexiones de entrada y salida se realizan con topología coaxial . La conexión entre una terminal de entrada y una salida no está permitida con la topología de puente normal y, por esta razón, se usa Twin-T donde de otra manera se usaría un puente para aplicaciones de medición de balance o nulos. La topología también se utiliza en el oscilador twin-T como generador de onda sinusoidal. La parte inferior de la figura 1.11 muestra la topología Twin-T rediseñada para enfatizar la conexión con la topología del puente.
Topologías infinitas
La topología de escalera se puede ampliar sin límites y se utiliza mucho en diseños de filtros. Existen muchas variaciones en la topología de escalera, algunas de las cuales se describen en los artículos Topología de filtro electrónico y Filtro de imagen compuesta .
La forma equilibrada de topología en escalera puede verse como el gráfico del lado de un prisma de orden arbitrario. El lado de un anti-prisma forma una topología que, en este sentido, es anti-escalera. La topología anti-escalera encuentra una aplicación en los circuitos multiplicadores de voltaje , en particular el generador Cockcroft-Walton . También hay una versión de onda completa del generador Cockcroft-Walton que utiliza una topología anti-escalera doble.
También se pueden formar topologías infinitas conectando en cascada múltiples secciones de alguna otra topología simple, como secciones de celosía o puente-T. Estas cadenas infinitas de secciones de celosía se producen en el análisis teórico y la simulación artificial de líneas de transmisión , pero rara vez se utilizan como implementación práctica de circuitos.
Componentes con más de dos terminales
Los circuitos que contienen componentes con tres o más terminales aumentan considerablemente el número de topologías posibles. Por el contrario, el número de circuitos diferentes representados por una topología disminuye y, en muchos casos, el circuito es fácilmente reconocible desde la topología incluso cuando no se identifican componentes específicos.

Figura 1.14 . Topología básica de amplificador , como amplificador de transistor de unión bipolar de emisor común
|

Figura 1.15 . Amplificador balanceado como un amplificador de par de cola larga
|
Con circuitos más complejos, la descripción puede proceder mediante la especificación de una función de transferencia entre los puertos de la red en lugar de la topología de los componentes.
Teoría de grafos
La teoría de grafos es la rama de las matemáticas que se ocupa de los grafos . En el análisis de redes, los gráficos se utilizan ampliamente para representar una red que se analiza. El gráfico de una red captura solo ciertos aspectos de una red; aquellos aspectos relacionados con su conectividad, es decir, su topología. Esta puede ser una representación y generalización útil de una red porque muchas ecuaciones de red son invariantes en redes con la misma topología. Esto incluye ecuaciones derivadas de las leyes de Kirchhoff y el teorema de Tellegen .
Historia
La teoría de grafos se ha utilizado en el análisis de redes de redes lineales pasivas casi desde el momento en que se formularon las leyes de Kirchhoff. El propio Gustav Kirchhoff , en 1847, utilizó gráficos como una representación abstracta de una red en su análisis de bucle de circuitos resistivos. Este enfoque se generalizó posteriormente a los circuitos RLC, reemplazando las resistencias por impedancias. En 1873, James Clerk Maxwell proporcionó el dual de este análisis con análisis de nodos. Maxwell también es responsable del teorema topológico de que el determinante de la matriz de admitancia de nodos es igual a la suma de todos los productos de admitancia del árbol. En 1900 Henri Poincaré introdujo la idea de representar un gráfico por su matriz de incidencia , fundando así el campo de la topología algebraica . En 1916 Oswald Veblen aplicó la topología algebraica de Poincaré al análisis de Kirchhoff. Veblen también es responsable de la introducción del árbol de expansión para ayudar a elegir un conjunto compatible de variables de red.
La catalogación completa de los gráficos de red que se aplican a los circuitos eléctricos comenzó con Percy MacMahon en 1891 (con un artículo amigable para los ingenieros en The Electrician en 1892), quien limitó su estudio a combinaciones en serie y en paralelo. MacMahon llamó a estos gráficos cadenas de yugo. Ronald M. Foster en 1932 categorizó los gráficos por su nulidad o rango y proporcionó gráficos de todos aquellos con un pequeño número de nodos. Este trabajo surgió de una encuesta anterior realizada por Foster mientras colaboraba con George Campbell en 1920 en repetidores telefónicos de 4 puertos y produjo 83,539 gráficos distintos.
Durante mucho tiempo, la topología en la teoría de circuitos eléctricos se mantuvo interesada únicamente en las redes lineales pasivas. Los desarrollos más recientes de circuitos y dispositivos semiconductores han requerido nuevas herramientas en topología para tratar con ellos. Los enormes aumentos en la complejidad de los circuitos han llevado al uso de la combinatoria en la teoría de grafos para mejorar la eficiencia del cálculo por computadora.
Gráficos y diagramas de circuitos
Las redes se clasifican comúnmente por el tipo de elementos eléctricos que las componen. En un diagrama de circuito, estos tipos de elementos se dibujan específicamente, cada uno con su propio símbolo único. Las redes resistivas son redes de un solo elemento, que constan solo de elementos R. Asimismo, las redes capacitivas o inductivas son de un solo elemento. Los circuitos RC , RL y LC son redes simples de dos elementos. El circuito RLC es la red de tres elementos más simple. La red de escalera LC comúnmente utilizada para filtros de paso bajo puede tener muchos elementos, pero es otro ejemplo de una red de dos elementos.
Por el contrario, la topología se ocupa únicamente de la relación geométrica entre los elementos de una red, no del tipo de elementos en sí. El corazón de una representación topológica de una red es el gráfico de la red. Los elementos se representan como los bordes del gráfico. Un borde se dibuja como una línea, que termina en puntos o círculos pequeños de los que pueden emanar otros bordes (elementos). En el análisis de circuitos, los bordes del gráfico se denominan ramas . Los puntos se denominan vértices del gráfico y representan los nodos de la red. Nodo y vértice son términos que se pueden usar indistintamente cuando se habla de gráficos de redes. La figura 2.2 muestra una representación gráfica del circuito de la figura 2.1.
Los gráficos utilizados en el análisis de redes suelen ser, además, gráficos dirigidos , para capturar la dirección del flujo de corriente y voltaje, y gráficos etiquetados , para capturar la singularidad de las ramas y nodos. Por ejemplo, un gráfico que consta de un cuadrado de ramas seguiría siendo el mismo gráfico topológico si se intercambiaran dos ramas, a menos que las ramas estuvieran etiquetadas de forma única. En los gráficos dirigidos, los dos nodos a los que se conecta una rama se designan como nodos de origen y de destino. Normalmente, estos se indicarán mediante una flecha dibujada en la rama.
Incidencia
La incidencia es una de las propiedades básicas de un gráfico. Se dice que una arista que está conectada a un vértice incide en ese vértice. La incidencia de un gráfico se puede capturar en formato de matriz con una matriz denominada matriz de incidencia. De hecho, la matriz de incidencia es una representación matemática alternativa del gráfico que prescinde de cualquier tipo de dibujo. Las filas de la matriz corresponden a los nodos y las columnas de la matriz corresponden a las ramas. Los elementos de la matriz son cero, para ninguna incidencia, o uno, para la incidencia entre el nodo y la rama. La dirección en los gráficos dirigidos se indica mediante el signo del elemento.
Equivalencia
Los gráficos son equivalentes si uno se puede transformar en otro por deformación. La deformación puede incluir las operaciones de traslación , rotación y reflexión ; doblar y estirar las ramas; y cruzar o anudar las ramas. Se dice que dos gráficos que son equivalentes por deformación son congruentes .
En el campo de las redes eléctricas, hay dos transformadas adicionales que se considera que dan como resultado gráficos equivalentes que no producen gráficos congruentes. El primero de ellos es el intercambio de ramas conectadas en serie. Este es el intercambio dual de ramas conectadas en paralelo que se puede lograr mediante deformación sin la necesidad de una regla especial. El segundo se refiere a gráficos divididos en dos o más partes separadas , es decir, un gráfico con dos conjuntos de nodos que no tienen ramas incidentes a un nodo en cada conjunto. Dos de estas partes separadas se consideran un gráfico equivalente a uno en el que las partes se unen combinando un nodo de cada una en un solo nodo. Del mismo modo, un gráfico que se puede dividir en dos partes separadas dividiendo un nodo en dos también se considera equivalente.
Árboles y enlaces
Un árbol es un gráfico en el que todos los nodos están conectados, directa o indirectamente, por ramas, pero sin formar bucles cerrados. Dado que no hay bucles cerrados, no hay corrientes en un árbol. En el análisis de redes, nos interesan los árboles de expansión , es decir, árboles que conectan todos los nodos presentes en el gráfico de la red. En este artículo, árbol de expansión se refiere a un árbol no calificado , a menos que se indique lo contrario. Un gráfico de red dado puede contener varios árboles diferentes. Las ramas que se quitan de un gráfico para formar un árbol se llaman enlaces , las ramas que quedan en el árbol se llaman ramitas . Para un gráfico con n nodos, el número de ramas en cada árbol, t , debe ser;
Una relación importante para el análisis de circuitos es;
donde b es el número de ramas en el gráfico y ℓ es el número de enlaces eliminados para formar el árbol.
Conjuntos de corbata y conjuntos de corte
El objetivo del análisis de circuitos es determinar todas las corrientes y tensiones derivadas de la red. Estas variables de red no son todas independientes. Los voltajes de los ramales están relacionados con las corrientes de los ramales por la función de transferencia de los elementos que los componen. Por lo tanto, una solución completa de la red puede ser en términos de corrientes de derivación o voltajes de derivación únicamente. Tampoco todas las corrientes de rama son independientes entre sí. El número mínimo de corrientes de derivación necesarias para una solución completa es l . Esto es una consecuencia del hecho de que un árbol tiene l enlaces eliminados y no puede haber ninguna corriente en un árbol. Dado que las ramas restantes del árbol tienen corriente cero, no pueden ser independientes de las corrientes de enlace. Las corrientes de rama elegidas como un conjunto de variables independientes deben ser un conjunto asociado con los enlaces de un árbol: no se puede elegir ninguna rama de l arbitrariamente.
En términos de voltajes de derivación, se puede obtener una solución completa de la red con t voltajes de derivación. Esto es una consecuencia del hecho de que el cortocircuito de todas las ramas de un árbol da como resultado que el voltaje sea cero en todas partes. Por lo tanto, los voltajes de enlace no pueden ser independientes de los voltajes de las ramas del árbol.
Un enfoque de análisis común es resolver las corrientes de bucle en lugar de las corrientes de derivación. Las corrientes de ramales se calculan luego en términos de las corrientes de bucle. Nuevamente, el conjunto de corrientes de lazo no se puede elegir arbitrariamente. Para garantizar un conjunto de variables independientes, las corrientes de bucle deben ser las asociadas con un determinado conjunto de bucles. Este conjunto de bucles está formado por aquellos que se forman al reemplazar un solo enlace de un árbol dado del gráfico del circuito a analizar. Dado que reemplazar un solo enlace en un árbol forma exactamente un bucle único, el número de corrientes de bucle así definido es igual a l . El término bucle en este contexto no es el mismo que el significado habitual de bucle en la teoría de grafos. El conjunto de ramas que forman un bucle determinado se denomina conjunto de ataduras . El conjunto de ecuaciones de red se forma equiparando las corrientes de bucle con la suma algebraica de las corrientes de ramificación del conjunto de conexiones.
Es posible elegir un conjunto de corrientes de lazo independientes sin hacer referencia a los árboles y conjuntos de ataduras. Una condición suficiente, pero no necesaria, para elegir un conjunto de bucles independientes es asegurarse de que cada bucle elegido incluya al menos una rama que no estaba incluida previamente en los bucles ya elegidos. Una elección particularmente sencilla es la que se utiliza en el análisis de mallas en el que todos los bucles se eligen como mallas. El análisis de malla solo se puede aplicar si es posible mapear el gráfico en un plano o una esfera sin que ninguna de las ramas se cruce. Estos gráficos se denominan gráficos planos . La capacidad de mapear en un plano o una esfera son condiciones equivalentes. Cualquier gráfico finito mapeado en un plano se puede reducir hasta que se mapee en una pequeña región de una esfera. Por el contrario, una malla de cualquier gráfico mapeado en una esfera se puede estirar hasta que el espacio dentro de ella ocupe casi toda la esfera. Entonces, el gráfico completo ocupa solo una pequeña región de la esfera. Esto es lo mismo que en el primer caso, por lo tanto, el gráfico también se mapeará en un plano.
Existe un enfoque para elegir variables de red con voltajes que es análogo y dual al método de corriente de bucle. Aquí el voltaje asociado con pares de nodos son las variables primarias y los voltajes de rama se encuentran en términos de ellos. En este método también, se debe elegir un árbol particular del gráfico para asegurar que todas las variables sean independientes. El doble del juego de corbata es el juego de corte . Un conjunto de vínculos se forma al permitir que todos los enlaces del gráfico, excepto uno, estén en circuito abierto. Un conjunto cortado se forma al permitir que todas las ramas de los árboles, excepto una, tengan un cortocircuito. El conjunto cortado consiste en la rama del árbol que no fue cortocircuitada y cualquiera de los enlaces que no están cortocircuitados por las otras ramas del árbol. Un conjunto cortado de un gráfico produce dos subgráficos inconexos , es decir, corta el gráfico en dos partes y es el conjunto mínimo de ramas necesarias para hacerlo. El conjunto de ecuaciones de red se forma equiparando los voltajes del par de nodos con la suma algebraica de los voltajes de rama del conjunto cortado. El dual del caso especial del análisis de malla es el análisis nodal .
Nulidad y rango
La nulidad, N , de un gráfico con s partes separadas y b ramas se define por;
La nulidad de un gráfico representa el número de grados de libertad de su conjunto de ecuaciones de red. Para un gráfico plano, la nulidad es igual al número de mallas en el gráfico.
El rango, R de un gráfico está definido por;
El rango juega el mismo papel en el análisis nodal que la nulidad en el análisis de malla. Es decir, da el número de ecuaciones de voltaje de nodo requeridas. El rango y la nulidad son conceptos duales y están relacionados por;
Resolviendo las variables de la red
Una vez que se ha elegido un conjunto de variables geométricamente independientes, el estado de la red se expresa en términos de estas. El resultado es un conjunto de ecuaciones lineales independientes que deben resolverse simultáneamente para encontrar los valores de las variables de la red. Este conjunto de ecuaciones se puede expresar en un formato de matriz que conduce a una matriz de parámetros característicos de la red. Las matrices de parámetros toman la forma de una matriz de impedancia si las ecuaciones se han formado sobre una base de análisis de bucle, o como una matriz de admitancia si las ecuaciones se han formado sobre una base de análisis de nodos.
Estas ecuaciones se pueden resolver de varias formas conocidas. Un método es la eliminación sistemática de variables . Otro método implica el uso de determinantes . Esto se conoce como regla de Cramer y proporciona una expresión directa para la variable desconocida en términos de determinantes. Esto es útil porque proporciona una expresión compacta para la solución. Sin embargo, para algo más que las redes más triviales, se requiere un mayor esfuerzo de cálculo para este método cuando se trabaja manualmente.
Dualidad
Dos gráficos son duales cuando la relación entre ramas y pares de nodos en uno es la misma que la relación entre ramas y bucles en el otro. El dual de un gráfico se puede encontrar completamente mediante un método gráfico .
El dual de un gráfico es otro gráfico. Para un árbol dado en un gráfico, el conjunto complementario de ramas (es decir, las ramas que no están en el árbol) forman un árbol en el gráfico dual. El conjunto de ecuaciones de bucle de corriente asociadas con los conjuntos de vínculos del gráfico y el árbol originales son idénticos al conjunto de ecuaciones de pares de nodos de voltaje asociados con los conjuntos de corte del gráfico dual.
La siguiente tabla enumera conceptos duales en topología relacionados con la teoría de circuitos.
| Actual | Voltaje |
| Árbol | Laberinto |
| Rama | Rama |
| Malla | Nodo |
| Círculo | Par de nodos |
| Enlace | Rama de árbol |
| Conjunto de corbata | Conjunto de corte |
| Cortocircuito | Circuito abierto |
| Coneccion paralela | Conexión en serie |
| Nulidad | Rango |
El dual de un árbol a veces se llama laberinto. Consiste en espacios conectados por enlaces de la misma manera que el árbol consta de nodos conectados por ramas de árboles.
No se pueden formar duales para todos los gráficos. La dualidad requiere que cada conjunto de corbatas tenga un conjunto de corte dual en el gráfico dual. Esta condición se cumple si y solo si el gráfico se puede mapear en una esfera sin ramas que se crucen. Para ver esto, tenga en cuenta que se requiere un conjunto de vínculos para "unir" un gráfico en dos porciones y su doble, el conjunto de corte, se requiere para cortar un gráfico en dos porciones. El gráfico de una red finita que no se mapeará en una esfera requerirá un toro n- pliegue . Un conjunto de empates que pase a través de un agujero en un toro no logrará unir el gráfico en dos partes. En consecuencia, el gráfico dual no se cortará en dos partes y no contendrá el conjunto de cortes requerido. En consecuencia, solo las gráficas planas tienen duales.
Tampoco se pueden formar duales para redes que contienen inductancias mutuas ya que no hay un elemento capacitivo correspondiente. Se pueden desarrollar circuitos equivalentes que tienen duales, pero el dual no puede formarse directamente de una inductancia mutua.
Eliminación de nodos y mallas
Las operaciones en un conjunto de ecuaciones de red tienen un significado topológico que puede ayudar a visualizar lo que está sucediendo. La eliminación de un voltaje de nodo de un conjunto de ecuaciones de red corresponde topológicamente a la eliminación de ese nodo del gráfico. Para un nodo conectado a otros tres nodos, esto corresponde a la bien conocida transformada Y-Δ . La transformación se puede extender a un mayor número de nodos conectados y luego se conoce como la transformación de malla de estrellas .
La inversa de esta transformada es la transformada Δ-Y que corresponde analíticamente a la eliminación de una corriente de malla y corresponde topológicamente a la eliminación de una malla. Sin embargo, la eliminación de una corriente de malla cuya malla tiene ramificaciones en común con un número arbitrario de otras mallas no dará, en general, un gráfico realizable. Esto se debe a que el gráfico de la transformación de la estrella general es un gráfico que no se mapeará en una esfera (contiene polígonos de estrellas y, por lo tanto, múltiples cruces). El dual de un gráfico de este tipo no puede existir, pero es el gráfico necesario para representar una eliminación de malla generalizada.
Acoplamiento mutuo

En la representación gráfica convencional de circuitos, no hay forma de representar explícitamente acoplamientos inductivos mutuos, como ocurre en un transformador , y tales componentes pueden dar como resultado un gráfico desconectado con más de una parte separada. Para facilitar el análisis, un gráfico con varias partes se puede combinar en un solo gráfico unificando un nodo en cada parte en un solo nodo. Esto no influye en el comportamiento teórico del circuito, por lo que el análisis realizado en él sigue siendo válido. Sin embargo, haría una diferencia práctica si un circuito se implementara de esta manera, ya que destruiría el aislamiento entre las partes. Un ejemplo sería un transformador conectado a tierra tanto en el lado primario como en el secundario. El transformador sigue funcionando como un transformador con la misma relación de voltaje, pero ahora ya no se puede utilizar como transformador de aislamiento .
Las técnicas más recientes de la teoría de grafos pueden tratar con componentes activos, que también son problemáticos en la teoría convencional. Estas nuevas técnicas también pueden hacer frente a acoplamientos mutuos.
Componentes activos
Hay dos enfoques básicos disponibles para tratar los acoplamientos mutuos y los componentes activos. En el primero de ellos, Samuel Jefferson Mason en 1953 introdujo gráficos de flujo de señales . Los gráficos de flujo de señales son gráficos dirigidos ponderados. Los utilizó para analizar circuitos que contienen acoplamientos mutuos y redes activas. El peso de un borde dirigido en estos gráficos representa una ganancia, como la que posee un amplificador. En general, los gráficos de flujo de señales, a diferencia de los gráficos dirigidos regulares descritos anteriormente, no se corresponden con la topología de la disposición física de los componentes.
El segundo enfoque consiste en ampliar el método clásico para que incluya acoplamientos mutuos y componentes activos. Se han propuesto varios métodos para lograr esto. En uno de estos, se construyen dos gráficos, uno representa las corrientes en el circuito y el otro representa los voltajes. Los componentes pasivos tendrán ramas idénticas en ambos árboles, pero es posible que los componentes activos no. El método se basa en identificar árboles de expansión que son comunes a ambos gráficos. Chen propuso en 1965 un método alternativo para ampliar el enfoque clásico que requiere sólo un gráfico. El método de Chen se basa en un árbol enraizado .
Hipergrafos
Otra forma de extender la teoría de grafos clásica para componentes activos es mediante el uso de hipergráficos . Algunos componentes electrónicos no se representan de forma natural mediante gráficos. El transistor tiene tres puntos de conexión, pero una rama de gráfico normal solo puede conectarse a dos nodos. Los circuitos integrados modernos tienen muchas más conexiones que esta. Este problema se puede solucionar utilizando hipergráficos en lugar de gráficos regulares.
En una representación convencional, los componentes están representados por bordes, cada uno de los cuales se conecta a dos nodos. En un hipergráfico, los componentes están representados por hiperexpresiones que pueden conectarse a un número arbitrario de nodos. Las crestas tienen tentáculos que conectan las crestas con los nodos. La representación gráfica de una hiperredge puede ser una caja (en comparación con el borde que es una línea) y las representaciones de sus tentáculos son líneas desde la caja a los nodos conectados. En un hipergrafo dirigido, los tentáculos llevan etiquetas que están determinadas por la etiqueta de la hipergrafia. Se puede pensar en un gráfico dirigido convencional como un hipergráfico con hipergrafos, cada uno de los cuales tiene dos tentáculos. Estos dos tentáculos están etiquetados como fuente y objetivo y generalmente se indican con una flecha. En un hipergráfico general con más tentáculos, se requerirá un etiquetado más complejo.
Los hipergráficos se pueden caracterizar por sus matrices de incidencia. Un gráfico regular que contiene solo componentes de dos terminales tendrá exactamente dos entradas distintas de cero en cada fila. Cualquier matriz de incidencia con más de dos entradas distintas de cero en cualquier fila es una representación de un hipergráfico. El número de entradas distintas de cero en una fila es el rango de la rama correspondiente, y el rango de rama más alto es el rango de la matriz de incidencia.
Variables no homogéneas
El análisis de red clásico desarrolla un conjunto de ecuaciones de red cuyas variables de red son homogéneas en corriente (análisis de bucle) o voltaje (análisis de nodo). El conjunto de variables de red así encontrado no es necesariamente el mínimo necesario para formar un conjunto de ecuaciones independientes. Puede haber una diferencia entre el número de variables en un análisis de bucle y un análisis de nodo. En algunos casos, el número mínimo posible puede ser menor que cualquiera de estos si el requisito de homogeneidad se relaja y se permite una combinación de variables de corriente y voltaje. Un resultado de Kishi y Katajini en 1967 es que el número mínimo absoluto de variables requeridas para describir el comportamiento de la red viene dado por la distancia máxima entre dos bosques en expansión del gráfico de red.
Síntesis de red
La teoría de grafos se puede aplicar a la síntesis de redes . La síntesis de red clásica realiza la red requerida en una de varias formas canónicas . Ejemplos de formas canónicas son la realización de una impedancia de punto de conducción por la red de escalera canónica de Cauer o la forma canónica de Foster o la realización de Brune de una inmitancia de sus funciones positivas-reales . Los métodos topológicos, por otro lado, no parten de una forma canónica determinada. Más bien, la forma es el resultado de la representación matemática. Algunas formas canónicas requieren inductancias mutuas para su realización. Un objetivo principal de los métodos topológicos de síntesis de redes ha sido eliminar la necesidad de estas inductancias mutuas. Un teorema que surge de la topología es que la realización de una impedancia de punto de excitación sin acoplamientos mutuos es mínima si y solo si no hay bucles totalmente inductores o totalmente condensadores.
La teoría de grafos es más poderosa en la síntesis de redes cuando los elementos de la red se pueden representar mediante números reales (redes de un solo elemento, como las redes resistivas) o estados binarios (como las redes de conmutación).
Redes infinitas
Quizás, la primera red con un gráfico infinito que se estudió fue la red en escalera utilizada para representar líneas de transmisión desarrollada, en su forma final, por Oliver Heaviside en 1881. Ciertamente, todos los estudios iniciales de redes infinitas se limitaron a estructuras periódicas como escaleras o cuadrículas con los mismos elementos repetidos una y otra vez. No fue hasta finales del siglo XX cuando se dispuso de herramientas para analizar redes infinitas con una topología arbitraria.
Las redes infinitas son en gran parte de interés sólo teórico y son el juguete de los matemáticos. Las redes infinitas que no están limitadas por restricciones del mundo real pueden tener algunas propiedades muy poco físicas. Por ejemplo, las leyes de Kirchhoff pueden fallar en algunos casos y se pueden definir escaleras de resistencias infinitas que tienen una impedancia de punto de activación que depende de la terminación en el infinito. Otra propiedad no física de las redes infinitas teóricas es que, en general, disiparán el poder infinito a menos que se les impongan restricciones además de las leyes de red habituales, como las leyes de Ohm y Kirchhoff. Sin embargo, existen algunas aplicaciones del mundo real. El ejemplo de la línea de transmisión pertenece a una clase de problemas prácticos que pueden modelarse mediante elementos infinitesimales (el modelo de elementos distribuidos ). Otros ejemplos son el lanzamiento de ondas a un medio continuo, problemas de campo periférico y medición de la resistencia entre puntos de un sustrato o en un pozo.
Las redes transfinitas amplían aún más la idea de redes infinitas. Un nodo en un extremo de una red infinita puede tener otra rama conectada que conduzca a otra red. Esta nueva red puede ser en sí misma infinita. Por lo tanto, se pueden construir topologías que tengan pares de nodos sin un camino finito entre ellos. Estas redes de redes infinitas se denominan redes transfinitas.
Notas
Ver también
Referencias
Bibliografía
- Brittain, James E., La introducción de la bobina de carga: George A. Campbell y Michael I. Pupin ", Tecnología y cultura , vol. 11 , núm. 1, págs. 36–57, The Johns Hopkins University Press, enero de 1970 doi : 10.2307 / 3102809 .
- Campbell, GA, "Teoría física del filtro de ondas eléctricas" , Bell System Technical Journal , noviembre de 1922, vol. 1, no. 2, págs. 1–32.
- Cederbaum, I., "Algunas aplicaciones de la teoría de grafos a análisis de la red y la síntesis" , IEEE Transactions on Circuitos y Sistemas , vol.31 , iss.1, pp. 64-68, Enero de 1.984.
- Farago, PS, Introducción al análisis de redes lineales , The English Universities Press Ltd, 1961.
- Foster, Ronald M., "Circuitos geométricos de redes eléctricas" , Transactions of the American Institute of Electrical Engineers , vol.51 , iss.2, pp. 309-317, junio de 1932.
- Foster, Ronald M .; Campbell, George A., "Redes de salida máxima para subestaciones telefónicas y circuitos repetidores" , Transactions of the American Institute of Electrical Engineers , vol.39 , iss.1, pp. 230-290, enero de 1920.
- Guillemin, Ernst A., Introducción a la teoría de circuitos , Nueva York: John Wiley & Sons, 1953 OCLC 535111
- Amable, Dieter; Feser, Kurt, Técnicas de prueba de alto voltaje , traductor Y. Narayana Rao, Newnes, 2001 ISBN 0-7506-5183-0 .
- Kishi, Genya; Kajitani, Yoji, "Árboles a máxima distancia y partición principal de un gráfico lineal" , IEEE Transactions on Circuit Theory , vol.16 , iss.3, pp. 323–330, agosto de 1969.
- MacMahon, Percy A., "Cadenas de yugo y composiciones multipartitas en relación con las formas analíticas llamadas" árboles "", Proceedings of the London Mathematical Society , vol.22 (1891), pp.330-346 doi : 10.1112 / plms / s1-22.1.330 .
- MacMahon, Percy A., "Combinations of resistances", The Electrician , vol.28 , pp. 601–602, 8 de abril de 1892.
Reimpreso en Discrete Applied Mathematics , vol.54 , iss.Iss.2–3, pp. 225 –228, 17 de octubre de 1994 doi : 10.1016 / 0166-218X (94) 90024-8 . - Minas, M., "Creación de representaciones semánticas de diagramas", Aplicaciones de transformaciones gráficas con relevancia industrial: taller internacional, AGTIVE'99, Kerkrade, Países Bajos, 1 al 3 de septiembre de 1999: actas , págs. 209–224, Springer, 2000 ISBN 3-540-67658-9 .
- Diario de radio de Redifon, 1970 , William Collins Sons & Co, 1969.
- Skiena, Steven S., Manual de diseño de algoritmos , Springer, 2008, ISBN 1-84800-069-3 .
- Suresh, Kumar KS, "Introducción a la topología de red" capítulo 11 en Circuitos y redes eléctricos , Pearson Education India, 2010 ISBN 81-317-5511-8 .
- Tooley, Mike, BTEC First Engineering: unidades opcionales obligatorias y seleccionadas para BTEC Firsts in Engineering , Routledge, 2010 ISBN 1-85617-685-1 .
- Wildes, Karl L .; Lindgren, Nilo A., "Análisis y síntesis de redes: Ernst A. Guillemin", Un siglo de ingeniería eléctrica y ciencias de la computación en MIT, 1882-1982 , págs. 154-159, MIT Press, 1985 ISBN 0-262-23119- 0 .
- Zemanian, Armen H., Infinite Electrical Networks , Cambridge University Press, 1991 ISBN 0-521-40153-4 .