Péndulo (mecánica) - Pendulum (mechanics)

Parte de una serie sobre
Mecanica clasica
${\ Displaystyle {\ textbf {F}} = {\ frac {d} {dt}} (m {\ textbf {v}})}$ Segunda ley del movimiento
Historia Cronología Libros de texto
Sucursales
Fundamentos
Formulaciones
Temas centrales
Rotación
Científicos
Portal de física  Categoría
v t mi

Un péndulo es un cuerpo suspendido de un soporte fijo de modo que se balancea libremente hacia adelante y hacia atrás bajo la influencia de la gravedad. Cuando un péndulo se desplaza lateralmente desde su posición de equilibrio de reposo, está sujeto a una fuerza restauradora debida a la gravedad que lo acelerará de regreso a la posición de equilibrio. Cuando se libera, la fuerza restauradora que actúa sobre la masa del péndulo hace que oscile alrededor de la posición de equilibrio, balanceándolo hacia adelante y hacia atrás. Las matemáticas de los péndulos son en general bastante complicadas. Se pueden hacer suposiciones simplificadoras, que en el caso de un péndulo simple permiten resolver analíticamente las ecuaciones de movimiento para oscilaciones de ángulo pequeño.

Péndulo de gravedad simple

Un péndulo de gravedad simple es un modelo matemático idealizado de un péndulo real. Este es un peso (o bob ) en el extremo de una cuerda sin masa suspendida de un pivote , sin fricción . Dado que en este modelo no hay pérdida de energía por fricción, cuando se le da un desplazamiento inicial, oscilará hacia adelante y hacia atrás con una amplitud constante . El modelo se basa en estos supuestos:

• La varilla o cuerda sobre la que se balancea el bob no tiene masa, es inextensible y siempre permanece tensa.
• La sacudida es una masa puntual.
• El movimiento se produce solo en dos dimensiones , es decir, la sacudida no traza una elipse sino un arco .
• El movimiento no pierde energía por fricción o resistencia del aire .
• El campo gravitacional es uniforme.
• El soporte no se mueve.

La ecuación diferencial que representa el movimiento de un péndulo simple es

${\ Displaystyle {\ frac {d ^ {2} \ theta} {dt ^ {2}}} + {\ frac {g} {\ ell}} \ sin \ theta = 0}$ Eq. 1

donde g es la magnitud del campo gravitacional , ℓ es la longitud de la varilla o cordón y θ es el ángulo de la vertical al péndulo.

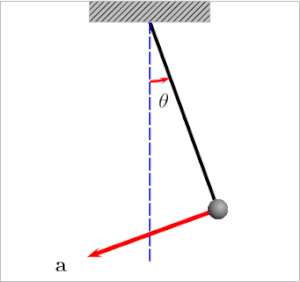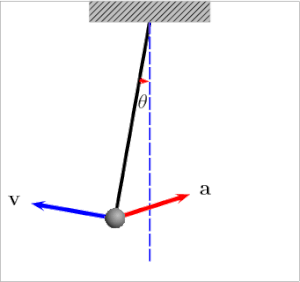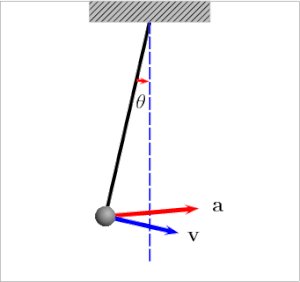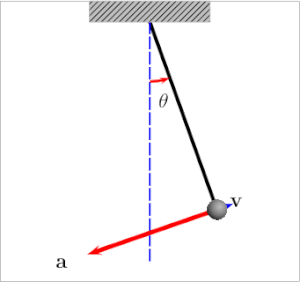
Derivación de la "fuerza" de ( Ec. 1 ) Figura 1. Diagrama de fuerza de un péndulo de gravedad simple. Considere la Figura 1 a la derecha, que muestra las fuerzas que actúan sobre un péndulo simple. Tenga en cuenta que la trayectoria del péndulo barre un arco de círculo. El ángulo θ se mide en radianes y esto es crucial para esta fórmula. La flecha azul es la fuerza gravitacional que actúa sobre el bob, y las flechas violetas son esa misma fuerza resuelta en componentes paralelos y perpendiculares al movimiento instantáneo del bob. La dirección de la velocidad instantánea de la sacudida siempre apunta a lo largo del eje rojo, que se considera el eje tangencial porque su dirección siempre es tangente al círculo. Considere la segunda ley de Newton , ${\ Displaystyle F = ma}$ donde F es la suma de las fuerzas sobre el objeto, m es la masa y a es la aceleración. Debido a que solo nos preocupan los cambios en la velocidad, y debido a que la sacudida se ve obligada a permanecer en una trayectoria circular, aplicamos la ecuación de Newton solo al eje tangencial. La flecha violeta corta representa el componente de la fuerza gravitacional en el eje tangencial y se puede usar la trigonometría para determinar su magnitud. Por lo tanto, ${\ displaystyle {\ begin {alineado} F & = - mg \ sin \ theta = ma, \ qquad {\ text {so}} \\ a & = - g \ sin \ theta, \ end {alineado}}}$ donde g es la aceleración debida a la gravedad cerca de la superficie de la tierra. El signo negativo en el lado derecho implica que θ y un siempre apuntan en direcciones opuestas. Esto tiene sentido porque cuando un péndulo se balancea más hacia la izquierda, esperaríamos que se acelerara hacia la derecha. Esta aceleración lineal a a lo largo del eje rojo se puede relacionar con el cambio de ángulo θ mediante las fórmulas de longitud de arco; s es la longitud del arco: ${\ Displaystyle {\ begin {alineado} s & = \ ell \ theta, \\ v & = {\ frac {ds} {dt}} = \ ell {\ frac {d \ theta} {dt}}, \\ a & = {\ frac {d ^ {2} s} {dt ^ {2}}} = \ ell {\ frac {d ^ {2} \ theta} {dt ^ {2}}}, \ end {alineado}}}$ por lo tanto: ${\ Displaystyle {\ begin {alineado} \ ell {\ frac {d ^ {2} \ theta} {dt ^ {2}}} & = - g \ sin \ theta, \\ {\ frac {d ^ {2 } \ theta} {dt ^ {2}}} + {\ frac {g} {\ ell}} \ sin \ theta & = 0. \ end {alineado}}}$

Derivación del "par" de ( Ec. 1 ) La ecuación (1) se puede obtener usando dos definiciones de torque. ${\ Displaystyle {\ boldsymbol {\ tau}} = \ mathbf {r} \ times \ mathbf {F} = {\ frac {d \ mathbf {L}} {dt}}.}$ Primero, comience por definir el par en el péndulo usando la fuerza debida a la gravedad. ${\ Displaystyle {\ boldsymbol {\ tau}} = \ mathbf {l} \ times \ mathbf {F} _ {\ mathrm {g}},}$ donde l es el vector de longitud del péndulo y F g es la fuerza debida a la gravedad. Por ahora, considere la magnitud del par en el péndulo. ${\ Displaystyle | {\ boldsymbol {\ tau}} | = -mg \ ell \ sin \ theta,}$ donde m es la masa del péndulo, g es la aceleración debida a la gravedad, l es la longitud del péndulo y θ es el ángulo entre el vector de longitud y la fuerza debida a la gravedad. A continuación, vuelva a escribir el momento angular. ${\ Displaystyle \ mathbf {L} = \ mathbf {r} \ times \ mathbf {p} = m \ mathbf {r} \ times ({\ boldsymbol {\ omega}} \ times \ mathbf {r}).}$ Una vez más, solo considere la magnitud del momento angular. ${\ Displaystyle | \ mathbf {L} | = señor ^ {2} \ omega = m \ ell ^ {2} {\ frac {d \ theta} {dt}}.}$ y su derivada del tiempo ${\ displaystyle {\ frac {d} {dt}} | \ mathbf {L} | = m \ ell ^ {2} {\ frac {d ^ {2} \ theta} {dt ^ {2}}},}$ Según τ = d L/dt, podemos obtener comparando las magnitudes ${\ Displaystyle -mg \ ell \ sin \ theta = m \ ell ^ {2} {\ frac {d ^ {2} \ theta} {dt ^ {2}}},}$ por lo tanto: ${\ Displaystyle {\ frac {d ^ {2} \ theta} {dt ^ {2}}} + {\ frac {g} {\ ell}} \ sin \ theta = 0,}$ que es el mismo resultado que se obtiene a través del análisis de fuerza.

Derivación de "energía" de ( Ec. 1 ) Figura 2. Trigonometría de un péndulo de gravedad simple. También se puede obtener mediante el principio de conservación de la energía mecánica : cualquier objeto que caiga una distancia vertical adquiriría una energía cinética igual a la que perdió en la caída. En otras palabras, la energía potencial gravitacional se convierte en energía cinética. El cambio en la energía potencial viene dado por ${\ Displaystyle h}$ ${\ Displaystyle \ Delta U = mgh. \,}$ El cambio en la energía cinética (el cuerpo partió del reposo) viene dado por ${\ Displaystyle \ Delta K = {\ tfrac {1} {2}} mv ^ {2}.}$ Dado que no se pierde energía, la ganancia en uno debe ser igual a la pérdida en el otro ${\ displaystyle {\ tfrac {1} {2}} mv ^ {2} = mgh. \,}$ El cambio de velocidad para un cambio de altura dado se puede expresar como ${\ Displaystyle v = {\ sqrt {2gh}}. \,}$ Usando la fórmula de longitud de arco anterior, esta ecuación se puede reescribir en términos de dθ/dt: ${\ Displaystyle {\ begin {alineado} v = \ ell {\ frac {d \ theta} {dt}} & = {\ sqrt {2gh}}, \ quad {\ text {so}} \\ {\ frac { d \ theta} {dt}} & = {\ frac {\ sqrt {2gh}} {l}}, \ end {alineado}}}$ donde h es la distancia vertical que cayó el péndulo. Mire la Figura 2, que presenta la trigonometría de un péndulo simple. Si el péndulo comienza su oscilación desde algún ángulo inicial θ 0 , entonces y 0 , la distancia vertical desde el tornillo, viene dada por ${\ Displaystyle y_ {0} = \ ell \ cos \ theta _ {0}. \,}$ De manera similar, para y 1 , tenemos ${\ Displaystyle y_ {1} = \ ell \ cos \ theta. \,}$ Entonces h es la diferencia de los dos ${\ Displaystyle h = \ ell \ left (\ cos \ theta - \ cos \ theta _ {0} \ right).}$ En términos de dθ/dt da ${\ displaystyle {\ frac {d \ theta} {dt}} = {\ sqrt {{\ frac {2g} {\ ell}} (\ cos \ theta - \ cos \ theta _ {0})}}.}$ Eq. 2 Esta ecuación se conoce como la primera integral de movimiento , da la velocidad en términos de la ubicación e incluye una constante de integración relacionada con el desplazamiento inicial ( θ 0 ). Podemos diferenciar, aplicando la regla de la cadena , con respecto al tiempo para obtener la aceleración ${\ Displaystyle {\ begin {alineado} {\ frac {d} {dt}} {\ frac {d \ theta} {dt}} & = {\ frac {d} {dt}} {\ sqrt {{\ frac {2g} {\ ell}} \ left (\ cos \ theta - \ cos \ theta _ {0} \ right)}}, \\ {\ frac {d ^ {2} \ theta} {dt ^ {2} }} & = {\ frac {1} {2}} {\ frac {- {\ frac {2g} {\ ell}} \ sin \ theta} {\ sqrt {{\ frac {2g} {\ ell}} (\ cos \ theta - \ cos \ theta _ {0})}}} {\ frac {d \ theta} {dt}} \\ & = {\ frac {1} {2}} {\ frac {- { \ frac {2g} {\ ell}} \ sin \ theta} {\ sqrt {{\ frac {2g} {\ ell}} (\ cos \ theta - \ cos \ theta _ {0})}}} {\ sqrt {{\ frac {2g} {\ ell}} (\ cos \ theta - \ cos \ theta _ {0})}} = - {\ frac {g} {\ ell}} \ sin \ theta, \\ {\ frac {d ^ {2} \ theta} {dt ^ {2}}} & + {\ frac {g} {\ ell}} \ sin \ theta = 0, \ end {alineado}}}$ que es el mismo resultado que se obtiene a través del análisis de fuerza.

Aproximación de ángulo pequeño

La ecuación diferencial dada anteriormente no se resuelve fácilmente y no hay una solución que se pueda escribir en términos de funciones elementales. Sin embargo, agregar una restricción al tamaño de la amplitud de la oscilación da una forma cuya solución se puede obtener fácilmente. Si se supone que el ángulo es mucho menor que 1  radianes (a menudo se cita como menos de 0,1 radianes, aproximadamente 6 °), o

${\ Displaystyle \ theta \ ll 1, \,}$

luego sustituyendo sin θ en la ecuación. 1 usando la aproximación de ángulo pequeño ,

${\ Displaystyle \ sin \ theta \ approx \ theta, \,}$

produce la ecuación para un oscilador armónico ,

${\ displaystyle {\ frac {d ^ {2} \ theta} {dt ^ {2}}} + {\ frac {g} {\ ell}} \ theta = 0.}$

El error debido a la aproximación es de orden θ ³ (de la expansión de Taylor para sen θ ).

Sea el ángulo inicial θ ₀ . Si se supone que el péndulo se libera con velocidad angular cero , la solución se convierte en

El movimiento es un movimiento armónico simple donde θ ₀ es la amplitud de la oscilación (es decir, el ángulo máximo entre la varilla del péndulo y la vertical). El período aproximado correspondiente del movimiento es entonces

que se conoce como la ley de Christiaan Huygens para el período. Tenga en cuenta que bajo la aproximación de ángulo pequeño, el período es independiente de la amplitud θ ₀ ; esta es la propiedad del isocronismo que descubrió Galileo .

Regla de oro para la longitud del péndulo

${\ Displaystyle T_ {0} = 2 \ pi {\ sqrt {\ frac {\ ell} {g}}}}$ se puede expresar como ${\ Displaystyle \ ell = {\ frac {g} {\ pi ^ {2}}} {\ frac {T_ {0} ^ {2}} {4}}.}$

Si se utilizan unidades SI (es decir, se miden en metros y segundos), y suponiendo que la medición se realiza en la superficie de la Tierra, entonces g ≈ 9,81 m / s ² , ygramo/π ²≈ 1 (0,994 es la aproximación a 3 decimales).

Por lo tanto, las aproximaciones relativamente razonables para la duración y el período son:

${\ displaystyle {\ begin {alineado} \ ell & \ approx {\ frac {T_ {0} ^ {2}} {4}}, \\ T_ {0} y \ approx 2 {\ sqrt {\ ell}} \ end {alineado}}}$

donde T ₀ es el número de segundos entre dos tiempos (un tiempo para cada lado del swing), y l se mide en metros.

Período de amplitud arbitraria

Para amplitudes más allá de la aproximación de ángulo pequeño , se puede calcular el período exacto invirtiendo primero la ecuación para la velocidad angular obtenida del método de la energía ( Ec. 2 ),

${\ Displaystyle {\ frac {dt} {d \ theta}} = {\ sqrt {\ frac {\ ell} {2g}}} {\ frac {1} {\ sqrt {\ cos \ theta - \ cos \ theta _ {0}}}}}$

y luego integrando en un ciclo completo,

${\ displaystyle T = t (\ theta _ {0} \ rightarrow 0 \ rightarrow - \ theta _ {0} \ rightarrow 0 \ rightarrow \ theta _ {0}),}$

o dos veces el medio ciclo

${\ displaystyle T = 2t (\ theta _ {0} \ rightarrow 0 \ rightarrow - \ theta _ {0}),}$

o cuatro veces el cuarto de ciclo

${\ Displaystyle T = 4t (\ theta _ {0} \ rightarrow 0),}$

lo que lleva a

${\ Displaystyle T = 4 {\ sqrt {\ frac {\ ell} {2g}}} \ int _ {0} ^ {\ theta _ {0}} {\ frac {1} {\ sqrt {\ cos \ theta - \ cos \ theta _ {0}}}} \, d \ theta.}$

Tenga en cuenta que esta integral diverge cuando θ _{0 se} acerca a la vertical

${\ Displaystyle \ lim _ {\ theta _ {0} \ rightarrow {\ frac {\ pi} {2}}} T = \ infty,}$

de modo que un péndulo con la energía justa para ir verticalmente nunca llegará allí. (Por el contrario, un péndulo cercano a su máximo puede tardar un tiempo arbitrariamente largo en caer).

Esta integral se puede reescribir en términos de integrales elípticas como

${\ Displaystyle T = 4 {\ sqrt {\ frac {\ ell} {g}}} F \ left ({\ frac {\ pi} {2}}, \ sin {\ frac {\ theta _ {0}} {2}} \ right)}$

donde F es la integral elíptica incompleta del primer tipo definida por

${\ Displaystyle F (\ varphi, k) = \ int _ {0} ^ {\ varphi} {\ frac {1} {\ sqrt {1-k ^ {2} \ sin ^ {2} u}}} \ , du \ ,.}$

O más concisamente por la sustitución

${\ Displaystyle \ sin {u} = {\ frac {\ sin {\ frac {\ theta} {2}}} {\ sin {\ frac {\ theta _ {0}} {2}}}}}$

expresando θ en términos de u ,

Aquí K es la integral elíptica completa del primer tipo definida por

${\ Displaystyle K (k) = F \ left ({\ frac {\ pi} {2}}, k \ right) = \ int _ {0} ^ {\ frac {\ pi} {2}} {\ frac {1} {\ sqrt {1-k ^ {2} \ sin ^ {2} u}}} \, du \ ,.}$

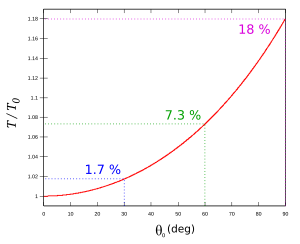
Para comparar la aproximación a la solución completa, considere el período de un péndulo de 1 m de longitud en la Tierra ( g =9.806 65  m / s ² ) en un ángulo inicial de 10 grados es

${\ Displaystyle 4 {\ sqrt {\ frac {1 {\ text {m}}} {g}}} \ K \ left (\ sin {\ frac {10 ^ {\ circ}} {2}} \ right) \ approx 2.0102 {\ text {s}}.}$

La aproximación lineal da

${\ Displaystyle 2 \ pi {\ sqrt {\ frac {1 {\ text {m}}} {g}}} \ approx 2.0064 {\ text {s}}.}$

La diferencia entre los dos valores, inferior al 0,2%, es mucho menor que la causada por la variación de g con la ubicación geográfica.

A partir de aquí hay muchas formas de proceder para calcular la integral elíptica.

Solución polinomial de Legendre para la integral elíptica

Dada la ecuación. 3 y la solución del polinomio de Legendre para la integral elíptica:

${\ Displaystyle K (k) = {\ frac {\ pi} {2}} \ sum _ {n = 0} ^ {\ infty} \ left ({\ frac {(2n-1) !!} {(2n ) !!}} k ^ {n} \ right) ^ {2}}$

donde n !! denota el factorial doble , una solución exacta al período de un péndulo simple es:

${\ displaystyle {\ begin {alignedat} {2} T & = 2 \ pi {\ sqrt {\ frac {\ ell} {g}}} \ left (1+ \ left ({\ frac {1} {2}} \ right) ^ {2} \ sin ^ {2} {\ frac {\ theta _ {0}} {2}} + \ left ({\ frac {1 \ cdot 3} {2 \ cdot 4}} \ right ) ^ {2} \ sin ^ {4} {\ frac {\ theta _ {0}} {2}} + \ left ({\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6 }} \ right) ^ {2} \ sin ^ {6} {\ frac {\ theta _ {0}} {2}} + \ cdots \ right) \\ & = 2 \ pi {\ sqrt {\ frac { \ ell} {g}}} \ cdot \ sum _ {n = 0} ^ {\ infty} \ left (\ left ({\ frac {(2n)!} {(2 ^ {n} \ cdot n!) ^ {2}}} \ right) ^ {2} \ cdot \ sin ^ {2n} {\ frac {\ theta _ {0}} {2}} \ right). \ End {alignedat}}}$

La Figura 4 muestra los errores relativos usando la serie de potencias. T ₀ es la aproximación lineal, y T ₂ a T ₁₀ incluyen respectivamente los términos hasta la 2ª a la 10ª potencias.

Solución de serie de potencia para la integral elíptica

Se puede encontrar otra formulación de la solución anterior si la siguiente serie de Maclaurin:

${\ Displaystyle \ sin {\ frac {\ theta _ {0}} {2}} = {\ frac {1} {2}} \ theta _ {0} - {\ frac {1} {48}} \ theta _ {0} ^ {3} + {\ frac {1} {3 \, 840}} \ theta _ {0} ^ {5} - {\ frac {1} {645 \, 120}} \ theta _ { 0} ^ {7} + \ cdots.}$

se utiliza en la solución polinomial de Legendre anterior. La serie de potencia resultante es:

${\ displaystyle {\ begin {alignedat} {2} T & = 2 \ pi {\ sqrt {\ frac {\ ell} {g}}} \ left (1 + {\ frac {1} {16}} \ theta _ {0} ^ {2} + {\ frac {11} {3 \, 072}} \ theta _ {0} ^ {4} + {\ frac {173} {737 \, 280}} \ theta _ {0 } ^ {6} + {\ frac {22 \, 931} {1 \, 321 \, 205 \, 760}} \ theta _ {0} ^ {8} + {\ frac {1 \, 319 \, 183 } {951 \, 268 \, 147 \, 200}} \ theta _ {0} ^ {10} + {\ frac {233 \, 526 \, 463} {2 \, 009 \, 078 \, 326 \, 886 \, 400}} \ theta _ {0} ^ {12} + \ cdots \ right) \ end {alignedat}}}$,

más fracciones disponibles en OEIS :  A223067 OEIS :  A223068 .

Solución de media aritmético-geométrica para integral elíptica

Dada la ecuación. 3 y la solución de la media aritmética-geométrica de la integral elíptica:

${\ Displaystyle K (k) = {\ frac {\ frac {\ pi} {2}} {M (1-k, 1 + k)}},}$

donde M ( x , y ) es la media aritmético-geométrica de x e y .

Esto produce una fórmula alternativa y de convergencia más rápida para el período:

${\ Displaystyle T = {\ frac {2 \ pi} {M \ left (1, \ cos {\ frac {\ theta _ {0}} {2}} \ right)}} {\ sqrt {\ frac {\ ell} {g}}}.}$

La primera iteración de este algoritmo da

${\ Displaystyle T_ {1} = {\ frac {2T_ {0}} {1+ \ cos {\ frac {\ theta _ {0}} {2}}}}.}$

Esta aproximación tiene un error relativo de menos del 1% para ángulos de hasta 96,11 grados. Dado que la expresión se puede escribir de forma más concisa como ${\ displaystyle {\ frac {1+ \ cos (\ theta _ {0} / 2)} {2}} = \ cos ^ {2} {\ frac {\ theta _ {0}} {4}},}$

${\ Displaystyle T_ {1} = T_ {0} \ sec ^ {2} {\ frac {\ theta _ {0}} {4}}.}$

La expansión de segundo orden de reduce a${\ Displaystyle \ sec ^ {2} (\ theta _ {0} / 4)}$${\ Displaystyle T \ approx T_ {0} \ left (1 + {\ frac {\ theta _ {0} ^ {2}} {16}} \ right).}$

Una segunda iteración de este algoritmo da

${\ Displaystyle T_ {2} = {\ frac {4T_ {0}} {1+ \ cos {\ frac {\ theta _ {0}} {2}} + 2 {\ sqrt {\ cos {\ frac {\ theta _ {0}} {2}}}}}} = {\ frac {4T_ {0}} {\ left (1 + {\ sqrt {\ cos {\ frac {\ theta _ {0}} {2} " }}} \ derecha) ^ {2}}}.}$

Esta segunda aproximación tiene un error relativo de menos del 1% para ángulos de hasta 163,10 grados.

Fórmulas aproximadas para el período del péndulo no lineal

Aunque el período exacto se puede determinar, para cualquier rad de amplitud finita , evaluando la integral elíptica completa correspondiente , donde esto a menudo se evita en las aplicaciones porque no es posible expresar esta integral en forma cerrada en términos de funciones elementales. Esto ha dado paso a la investigación de fórmulas aproximadas simples para el aumento del período del péndulo con amplitud (útiles en laboratorios de introducción a la física, mecánica clásica, electromagnetismo, acústica, electrónica, superconductividad, etc. Las fórmulas aproximadas encontradas por diferentes autores se pueden clasificar como sigue: ${\ Displaystyle T}$${\ Displaystyle \ theta _ {0} <\ pi}$${\ Displaystyle K (k)}$${\ Displaystyle k \ equiv \ sin (\ theta _ {0} / 2)}$

• Fórmulas de 'ángulo no tan grande', es decir, aquellas que producen buenas estimaciones para amplitudes por debajo de rad (un límite natural para una sacudida en el extremo de una cuerda flexible), aunque la desviación con respecto al período exacto aumenta monótonamente con la amplitud, siendo inadecuadas para amplitudes cercanas a rad. Una de las fórmulas más simples encontradas en la literatura es la siguiente de Lima (2006):, donde .${\ Displaystyle \ pi / 2}$${\ Displaystyle \ pi}$${\ Displaystyle T \ approx - \, T_ {0} \, {\ frac {\ ln {a}} {1-a}}}$${\ Displaystyle a \ equiv \ cos {(\ theta _ {0} / 2)}}$

• Fórmulas de 'ángulo muy grande', es decir, aquellas que se aproximan asintóticamente al período exacto para amplitudes cercanas a rad, con un error que aumenta monótonamente para amplitudes más pequeñas (es decir, inadecuadas para amplitudes pequeñas). Uno de los mejor tales fórmulas es que por Cromer, a saber: .${\ Displaystyle \ pi}$${\ Displaystyle T \ approx {\ frac {2} {\ pi}} \, T_ {0} \, \ ln {(4 / a)}}$

Por supuesto, el aumento de con amplitud es más evidente cuando , como se ha observado en muchos experimentos, se usa una varilla rígida o un disco. Como actualmente se dispone de temporizadores y sensores precisos incluso en los laboratorios de introducción a la física, los errores experimentales que se encuentran en los experimentos de 'ángulos muy grandes' ya son lo suficientemente pequeños para una comparación con el período exacto y una muy buena concordancia entre la teoría y los experimentos en los que se produce fricción. se ha encontrado insignificante. Dado que esta actividad ha sido impulsada por muchos instructores, se buscó una fórmula aproximada simple para el período del péndulo válida para todas las amplitudes posibles, con la que se pudieran comparar los datos experimentales. En 2008, Lima derivó una fórmula de promedio ponderado con esta característica: ${\ Displaystyle T}$${\ Displaystyle \ pi / 2 <\ theta _ {0} <\ pi}$

${\ Displaystyle T \ approx {\ frac {r \, a ^ {2} \, T_ {Lima} + k ^ {2} \, T_ {Cromer}} {r \, a ^ {2} + k ^ { 2}}}}$,

donde , que presenta un error máximo de solo 0,6% (at ). ${\ Displaystyle r = 7.17}$${\ Displaystyle \ theta _ {0} = 95 ^ {\ circ}}$

Desplazamiento angular de amplitud arbitraria Serie de Fourier

La expansión de la serie de Fourier de está dada por ${\ Displaystyle \ theta (t)}$

${\ Displaystyle \ theta (t) = 8 \ sum _ {n \ geq 1 {\ text {impar}}} {\ frac {(-1) ^ {\ left \ lfloor {n / 2} \ right \ rfloor} } {n}} {\ frac {q ^ {n / 2}} {1 + q ^ {n}}} \ cos (n \ omega t)}$

donde es el nome elíptica , y la frecuencia angular. ${\ Displaystyle q}$${\ Displaystyle q = \ exp (- \ pi K '/ K)}$${\ Displaystyle \ omega = 2 \ pi / T}$

Si uno define

${\ Displaystyle \ epsilon = {\ frac {1 - {\ sqrt {\ cos {\ frac {\ theta _ {0}} {2}}}}} {2 + 2 {\ sqrt {\ cos {\ frac { \ theta _ {0}} {2}}}}}}}$

${\ Displaystyle q}$ se puede aproximar usando la expansión

${\ displaystyle q = \ epsilon +2 \ epsilon ^ {5} +15 \ epsilon ^ {9} +150 \ epsilon ^ {13} +1707 \ epsilon ^ {17} +20910 \ epsilon ^ {21} + \ cdots }$

(ver OEIS :  A002103 ). Tenga en cuenta que, por lo que tenemos , la aproximación es aplicable incluso para grandes amplitudes. ${\ Displaystyle \ theta _ {0} <\ pi}$${\ Displaystyle \ epsilon <{\ tfrac {1} {2}}}$

Ejemplos de

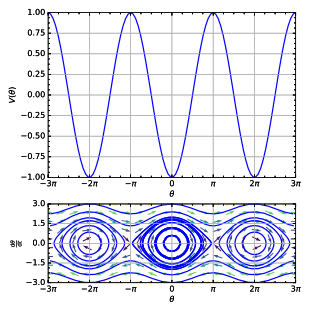
Las animaciones siguientes representan el movimiento de un péndulo simple (sin fricción) con cantidades crecientes de desplazamiento inicial de la sacudida, o equivalentemente aumentando la velocidad inicial. El pequeño gráfico sobre cada péndulo es el diagrama de plano de fase correspondiente ; el eje horizontal es el desplazamiento y el eje vertical es la velocidad. Con una velocidad inicial lo suficientemente grande, el péndulo no oscila hacia adelante y hacia atrás, sino que gira completamente alrededor del pivote.

• 

  Ángulo inicial de 0 °, un equilibrio estable

• 

  Ángulo inicial de 45 °

• 

  Ángulo inicial de 90 °

• 

  Ángulo inicial de 135 °

• 

  Ángulo inicial de 170 °

• 

  Ángulo inicial de 180 °, equilibrio inestable

• 

  Péndulo con apenas energía suficiente para un swing completo

• 

  Péndulo con suficiente energía para un swing completo

Péndulo compuesto

Un péndulo compuesto (o péndulo físico ) es aquel en el que la varilla no carece de masa y puede tener un tamaño extendido; es decir, un cuerpo rígido de forma arbitraria que se balancea mediante un pivote. En este caso, el período del péndulo depende de su momento de inercia I alrededor del punto de pivote.

La ecuación de torque da:

${\ Displaystyle \ tau = I \ alpha \,}$

dónde:

α es la aceleración angular.

τ es el par

El par se genera por gravedad, por lo que:

${\ Displaystyle \ tau = -mgL \ sin \ theta \,}$

dónde:

m es la masa del cuerpo

L es la distancia desde el pivote hasta el centro de masa del objeto

θ es el ángulo de la vertical

Por lo tanto, bajo la aproximación de ángulo pequeño sin θ ≈ θ ,

${\ Displaystyle \ alpha = {\ ddot {\ theta}} \ approx - {\ frac {mgL \ theta} {I}}}$

donde I es el momento de inercia del cuerpo alrededor del punto de pivote.

La expresión para α tiene la misma forma que el péndulo simple convencional y da un período de

${\ Displaystyle T = 2 \ pi {\ sqrt {\ frac {I} {mgL}}}}$

Y una frecuencia de

${\ Displaystyle f = {\ frac {1} {T}} = {\ frac {1} {2 \ pi}} {\ sqrt {\ frac {mgL} {I}}}}$

Si se toma en consideración el ángulo inicial (para grandes amplitudes), entonces la expresión para se convierte en: ${\ Displaystyle \ alpha}$

${\ Displaystyle \ alpha = {\ ddot {\ theta}} = - {\ frac {mgL \ sin \ theta} {I}}}$

y da un período de:

${\ Displaystyle T = 4 \ operatorname {K} \ left (\ sin ^ {2} {\ frac {\ theta _ {0}} {2}} \ right) {\ sqrt {\ frac {I} {mgL} }}}$

donde θ ₀ es el ángulo máximo de oscilación (con respecto a la vertical) y K ( k ) es la integral elíptica completa del primer tipo .

Interpretación física del período imaginario

La función elíptica jacobiana que expresa la posición de un péndulo en función del tiempo es una función doblemente periódica con un período real y un período imaginario . El período real es, por supuesto, el tiempo que tarda el péndulo en recorrer un ciclo completo. Paul Appell señaló una interpretación física del período imaginario: si θ ₀ es el ángulo máximo de un péndulo y 180 ° - θ ₀ es el ángulo máximo de otro, entonces el período real de cada uno es la magnitud del período imaginario de la otro.

Péndula acoplada

Los péndulos acoplados pueden afectar el movimiento de los demás, ya sea a través de una conexión de dirección (como un resorte que conecta las sacudidas) o mediante movimientos en una estructura de soporte (como una mesa). Las ecuaciones de movimiento para dos péndulos simples idénticos acoplados por un resorte que conecta las sacudidas se pueden obtener utilizando la Mecánica Lagrangiana .

La energía cinética del sistema es:

${\ Displaystyle E _ {\ text {K}} = {\ frac {1} {2}} mL ^ {2} \ left ({\ dot {\ theta}} _ {1} ^ {2} + {\ dot {\ theta}} _ {2} ^ {2} \ right)}$

donde es la masa de las sacudidas, es la longitud de las cuerdas y , son los desplazamientos angulares de las dos sacudidas desde el equilibrio. ${\ Displaystyle m}$${\ Displaystyle L}$${\ Displaystyle \ theta _ {1}}$${\ Displaystyle \ theta _ {2}}$

La energía potencial del sistema es:

${\ Displaystyle E _ {\ text {p}} = mgL (2- \ cos \ theta _ {1} - \ cos \ theta _ {2}) + {\ frac {1} {2}} kL ^ {2} (\ theta _ {2} - \ theta _ {1}) ^ {2}}$

donde es la aceleración gravitacional y es la constante del resorte . El desplazamiento del resorte desde su posición de equilibrio asume la aproximación de ángulo pequeño . ${\ Displaystyle g}$${\ Displaystyle k}$${\ Displaystyle L (\ theta _ {2} - \ theta _ {1})}$

El lagrangiano es entonces

${\ Displaystyle {\ mathcal {L}} = {\ frac {1} {2}} mL ^ {2} \ left ({\ dot {\ theta}} _ {1} ^ {2} + {\ dot { \ theta}} _ {2} ^ {2} \ right) -mgL (2- \ cos \ theta _ {1} - \ cos \ theta _ {2}) - {\ frac {1} {2}} kL ^ {2} (\ theta _ {2} - \ theta _ {1}) ^ {2}}$

lo que conduce al siguiente conjunto de ecuaciones diferenciales acopladas:

${\ Displaystyle {\ begin {alineado} {\ ddot {\ theta}} _ {1} + {\ frac {g} {L}} \ sin \ theta _ {1} + {\ frac {k} {m} } (\ theta _ {1} - \ theta _ {2}) & = 0 \\ {\ ddot {\ theta}} _ {2} + {\ frac {g} {L}} \ sin \ theta _ { 2} - {\ frac {k} {m}} (\ theta _ {1} - \ theta _ {2}) & = 0 \ end {alineado}}}$

Sumando y restando estas dos ecuaciones sucesivamente, y aplicando la aproximación de ángulo pequeño, se obtienen dos ecuaciones de oscilador armónico en las variables y : ${\ Displaystyle \ theta _ {1} + \ theta _ {2}}$${\ Displaystyle \ theta _ {1} - \ theta _ {2}}$

${\ Displaystyle {\ begin {alineado} {\ ddot {\ theta}} _ {1} + {\ ddot {\ theta}} _ {2} + {\ frac {g} {L}} (\ theta _ { 1} + \ theta _ {2}) & = 0 \\ {\ ddot {\ theta}} _ {1} - {\ ddot {\ theta}} _ {2} + \ left ({\ frac {g} {L}} + 2 {\ frac {k} {m}} \ derecha) (\ theta _ {1} - \ theta _ {2}) & = 0 \ end {alineado}}}$

con las soluciones correspondientes

${\ Displaystyle {\ begin {alineado} \ theta _ {1} + \ theta _ {2} & = A \ cos (\ omega _ {1} t + \ alpha) \\\ theta _ {1} - \ theta _ {2} & = B \ cos (\ omega _ {2} t + \ beta) \ end {alineado}}}$

dónde

${\ Displaystyle {\ begin {alineado} \ omega _ {1} & = {\ sqrt {\ frac {g} {L}}} \\\ omega _ {2} & = {\ sqrt {{\ frac {g } {L}} + 2 {\ frac {k} {m}}}} \ end {alineado}}}$

y , , , son constantes de integración . ${\ Displaystyle A}$${\ Displaystyle B}$${\ Displaystyle \ alpha}$${\ Displaystyle \ beta}$

Expresando las soluciones en términos de y solo: ${\ Displaystyle \ theta _ {1}}$${\ Displaystyle \ theta _ {2}}$

${\ Displaystyle {\ begin {alineado} \ theta _ {1} & = {\ frac {1} {2}} A \ cos (\ omega _ {1} t + \ alpha) + {\ frac {1} {2 }} B \ cos (\ omega _ {2} t + \ beta) \\\ theta _ {2} & = {\ frac {1} {2}} A \ cos (\ omega _ {1} t + \ alpha) - {\ frac {1} {2}} B \ cos (\ omega _ {2} t + \ beta) \ end {alineado}}}$

Si los bobs no reciben un empujón inicial, entonces la condición requiere , lo que da (después de algunas reorganizaciones): ${\ displaystyle {\ dot {\ theta}} _ {1} (0) = {\ dot {\ theta}} _ {2} (0) = 0}$${\ Displaystyle \ alpha = \ beta = 0}$

${\ Displaystyle {\ begin {alineado} A & = \ theta _ {1} (0) + \ theta _ {2} (0) \\ B & = \ theta _ {1} (0) - \ theta _ {2} (0) \ end {alineado}}}$

Ver también

• Péndulo de Blackburn
• Péndulo cónico
• Péndulo cicloidal
• Péndulo doble
• Péndulo invertido
• Péndulo de Kapitza
• Péndulo de Rayleigh-Lorentz
• Péndulo de primavera
• Función de Mathieu
• Ecuaciones de péndulo (software)

Referencias

Otras lecturas

• Baker, Gregory L .; Blackburn, James A. (2005). El péndulo: un estudio de caso de física (PDF) . Prensa de la Universidad de Oxford.
• Ochs, Karlheinz (2011). "Una solución analítica integral del péndulo no lineal". Revista europea de física . 32 (2): 479–490. Código Bibliográfico : 2011EJPh ... 32..479O . doi : 10.1088 / 0143-0807 / 32/2/019 .
• Sala, Kenneth L. (1989). "Transformaciones de la función de amplitud jacobiana y su cálculo mediante la media aritmético-geométrica". SIAM J. Math. Anal . 20 (6): 1514-1528. doi : 10.1137 / 0520100 .

enlaces externos

• Artículo de Mathworld sobre la función Mathieu