Huesos de Napier - Napier's bones
| Dispositivos informáticos en |
| Rabdología |
|---|
| Huesos de Napier |
| Promptuary |
| Aritmética de ubicación |
Los huesos de Napier son un dispositivo de cálculo operado manualmente creado por John Napier de Merchiston , Escocia para el cálculo de productos y cocientes de números. El método se basaba en la multiplicación reticular y también se llamaba "rabdología", palabra inventada por Napier. Napier publicó su versión en 1617. impresa en Edimburgo , dedicada a su mecenas Alexander Seton .
Usando las tablas de multiplicar incrustadas en las varillas, la multiplicación se puede reducir a operaciones de suma y la división a restas. El uso avanzado de las varillas puede extraer raíces cuadradas . Los huesos de Napier no son lo mismo que los logaritmos , con los que también está asociado el nombre de Napier, sino que se basan en tablas de multiplicar diseccionadas.
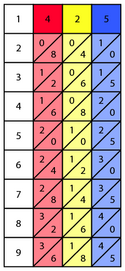
El dispositivo completo generalmente incluye una placa base con un borde; el usuario coloca las varillas de Napier dentro del borde para realizar la multiplicación o división. El borde izquierdo del tablero está dividido en nueve cuadrados, con los números del 1 al 9. En el diseño original de Napier, las varillas están hechas de metal, madera o marfil y tienen una sección transversal cuadrada. Cada barra está grabada con una tabla de multiplicar en cada una de las cuatro caras. En algunos diseños posteriores, las varillas son planas y tienen dos mesas o solo una grabada en ellas, y están hechas de plástico o cartón pesado. Un juego de esos huesos podría estar encerrado en un estuche de transporte.
La cara de una barra está marcada con nueve cuadrados. Cada cuadrado, excepto el superior, está dividido en dos mitades por una línea diagonal desde la esquina inferior izquierda hasta la esquina superior derecha. Los cuadrados contienen una tabla de multiplicar simple. El primero tiene un solo dígito, que Napier llamó el "sencillo". Los otros contienen los múltiplos del sencillo, es decir, dos veces el sencillo, tres veces el sencillo y así sucesivamente hasta el noveno cuadrado que contiene nueve veces el número en el cuadrado superior. Los números de un solo dígito se escriben en el triángulo inferior derecho dejando el otro triángulo en blanco, mientras que los números de dos dígitos se escriben con un dígito a cada lado de la diagonal.
Si las tablas se mantienen en barras de un solo lado, se necesitan 40 barras para multiplicar números de 4 dígitos; dado que los números pueden tener dígitos repetidos, se necesitan cuatro copias de la tabla de multiplicar para cada uno de los dígitos del 0 al 9. Si se utilizan barras cuadradas, las 40 tablas de multiplicar se pueden inscribir en 10 barras. Napier dio detalles de un esquema para organizar las mesas de modo que ninguna barra tenga dos copias de la misma tabla, permitiendo que cada número posible de cuatro dígitos sea representado por 4 de las 10 barras. Un conjunto de 20 barras, que consta de dos copias idénticas de las 10 barras de Napier, permite el cálculo con números de hasta ocho dígitos, y se puede utilizar un conjunto de 30 barras para números de 12 dígitos.
Multiplicación
El tipo de multiplicación más simple, un número de varios dígitos por un número de un solo dígito, se realiza colocando barras que representan el número de varios dígitos en el marco contra el borde izquierdo. La respuesta se lee en la fila correspondiente al número de un solo dígito que está marcado a la izquierda del cuadro, con una pequeña cantidad de adición requerida, como se explica en los ejemplos a continuación.
Al multiplicar un número de varios dígitos por otro número de varios dígitos, el número más grande se configura en las varillas del marco. El dispositivo produce un resultado intermedio para la multiplicación por cada uno de los dígitos del número menor. Estos se anotan y el resultado final se calcula con lápiz y papel.
Para demostrar cómo usar los huesos de Napier para la multiplicación, a continuación se explican tres ejemplos de dificultad creciente.
Ejemplo 1: multiplicación por un número pequeño de un solo dígito
El primer ejemplo calcula 425 × 6 .
Los huesos de Napier para 4, 2 y 5 se colocan en el tablero. Se multiplican los huesos del número mayor. Como ejemplo de los valores que se derivan de las tablas de multiplicar, los valores de la séptima fila del hueso 4 serían 2 ⁄ 8 , derivado de 7 × 4 = 28 . En el siguiente ejemplo para 425 × 6 , los huesos se representan en rojo, amarillo y azul, respectivamente.
La columna más a la izquierda antes de cualquiera de los huesos podría representarse como el hueso 1, que tendría un espacio en blanco o cero en la parte superior izquierda separada por una línea diagonal, ya que 1 × 1 = 01 , 1 × 2 = 02 , 1 x 3 = 03 , etc. Se elige un número pequeño, generalmente del 2 al 9, por el cual multiplicar el número grande. En este ejemplo, el número pequeño que se multiplica por es 6. La fila en la que se encuentra este número es la única fila necesaria para realizar los cálculos restantes y, por lo tanto, generalmente se aísla del resto del tablero para mayor claridad.
El cálculo se puede iniciar desde cualquier extremo. Los valores separados por líneas verticales se suman para formar los dígitos de los productos. El último número encontrado en esa fila horizontal de huesos nunca requerirá suma, ya que siempre está aislado por la última línea. Siempre se encontrará en el "lugar de uno" del producto. Para los otros dígitos, se suman los dos números de huesos adyacentes separados por líneas verticales. En este ejemplo, hay cuatro dígitos, ya que hay cuatro grupos de valores óseos separados por líneas. Los dígitos del producto van en el mismo orden en que se calculan. Además del último (o primer) dígito, los dígitos del producto serán la suma de dos valores tomados de dos huesos diferentes.
Los valores óseos se suman para obtener los dígitos del producto. El tercer dígito de producto de los huesos amarillo y azul tiene sus valores relevantes de color verde. Cada suma está escrita en el espacio a continuación. Los resultados de las sumas de izquierda a derecha producen la respuesta final de 2550. Por lo tanto, la solución para multiplicar 425 por 6 es 2550.
Ejemplo 2: multiplicación por un número más grande de un solo dígito
Al multiplicar por dígitos individuales más grandes, es común que al agregar una columna diagonal, la suma de los números resulte en un número de 10 o más.
El segundo ejemplo calcula 6785 × 8 .
Como en el ejemplo 1, los huesos correspondientes al número más grande se colocan en el tablero. Para este ejemplo, los huesos 6, 7, 8 y 5 se colocaron en el orden correcto como se muestra a continuación.
En la primera columna, se encuentra el número por el que se multiplica el número más grande. En este ejemplo, el número era 8. Solo la fila 8 se usará para los cálculos restantes, por lo que el resto del tablero se ha limpiado para aclarar la explicación de los pasos restantes.
Al igual que antes, se evalúa cada columna diagonal, comenzando por el lado derecho. Si la suma de una columna diagonal es igual a 10 o más, el lugar de las "decenas" de esta suma debe transferirse y sumarse junto con los números en la columna izquierda adyacente como se muestra a continuación.
Después de evaluar cada columna diagonal, los números calculados se leen de izquierda a derecha para producir una respuesta final; en este ejemplo, se produjo 54280.
Por lo tanto: La solución para multiplicar 6785 por 8 es 54280.
Ejemplo 3: multiplicación por un número de varios dígitos
El tercer ejemplo calcula 825 × 913 .
Los huesos correspondientes al número principal se colocan en el tablero. Para este ejemplo, los huesos 8, 2 y 5 se colocaron en el orden correcto como se muestra a continuación.
Para multiplicar por un número de varios dígitos, se revisan varias filas. Para este ejemplo, las filas para 9, 1 y 3 se han eliminado del tablero para mayor claridad.
Cada fila se evalúa individualmente y cada columna diagonal se agrega como se explica en los ejemplos anteriores. Las sumas se leen de izquierda a derecha, produciendo los números necesarios para los siguientes cálculos de suma a mano. Para este ejemplo, la fila 9, la fila 1 y la fila 3 se evaluaron por separado para producir los resultados que se muestran a continuación.
Comenzando con el dígito más a la derecha del segundo número, las sumas se colocan desde las filas en orden secuencial como se ve de derecha a izquierda una debajo de la otra mientras se utiliza un 0 como marcador de posición.
2475 8250 742500
Las filas y los marcadores de posición se suman para producir una respuesta final.
2475
8250
+ 742500
753225
En este ejemplo, la respuesta final fue 753225. Por lo tanto: La solución para multiplicar 825 por 913 es 753225.
División
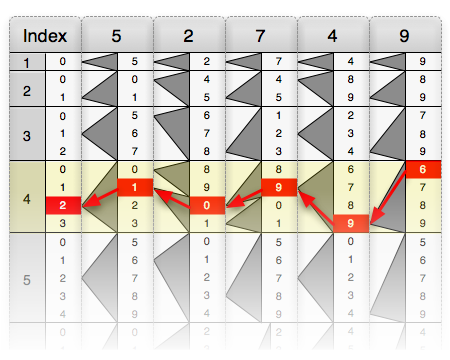
La división se realiza de manera similar. Para dividir 46785399 por 96431, las barras del divisor (96431) se colocan en el tablero, como se muestra en el gráfico siguiente. Usando el ábaco, todos los productos del divisor del 1 al 9 se encuentran leyendo los números mostrados. Tenga en cuenta que el dividendo tiene ocho dígitos, mientras que los productos parciales (excepto el primero) tienen seis. Por lo tanto, los dos últimos dígitos de 46785399, es decir, el '99', se ignoran temporalmente, dejando el número 467853. Luego, se encuentra el mayor producto parcial que es menor que el dividendo truncado. En este caso, 385724. Se deben marcar dos cosas, como se ve en el diagrama: dado que 385724 está en la fila '4' del ábaco, un '4' se marca como el dígito más a la izquierda del cociente; también se escribe el producto parcial, alineado a la izquierda, debajo del dividendo original. Se restan los dos términos, lo que deja 8212999. Se repiten los mismos pasos: el número se trunca a seis dígitos, se elige el producto parcial inmediatamente menor que el número truncado, el número de fila se escribe como el siguiente dígito del cociente, y el producto parcial se resta de la diferencia encontrada en la primera repetición. El proceso se muestra en el diagrama. El ciclo se repite hasta que el resultado de la resta sea menor que el divisor. El número que queda es el resto.
Entonces, en este ejemplo, lo que queda es un cociente de 485 con un resto de 16364. El proceso generalmente se detiene aquí y la respuesta usa la forma fraccionaria 485+16364/96431.
Para mayor precisión, el ciclo continúa para encontrar tantos lugares decimales necesarios. Se marca un punto decimal después del último dígito del cociente y se agrega un cero al resto que deja 163640. El ciclo continúa, cada vez que se agrega un cero al resultado después de la resta.
Extrayendo raíces cuadradas
Para extraer la raíz cuadrada se utiliza un hueso adicional que se diferencia de los demás por tener tres columnas. La primera columna tiene los primeros nueve números cuadrados, la segunda tiene los primeros nueve números pares y la última tiene los números del 1 al 9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | √ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 ⁄ 1 | 0 ⁄ 2 | 0 ⁄ 3 | 0 ⁄ 4 | 0 ⁄ 5 | 0 ⁄ 6 | 0 ⁄ 7 | 0 ⁄ 8 | 0 ⁄ 9 | 0 ⁄ 1 2 1 |
| 2 | 0 ⁄ 2 | 0 ⁄ 4 | 0 ⁄ 6 | 0 ⁄ 8 | 1 ⁄ 0 | 1 ⁄ 2 | 1 ⁄ 4 | 1 ⁄ 6 | 1 ⁄ 8 | 0 ⁄ 4 4 2 |
| 3 | 0 ⁄ 3 | 0 ⁄ 6 | 0 ⁄ 9 | 1 ⁄ 2 | 1 ⁄ 5 | 1 ⁄ 8 | 2 ⁄ 1 | 2 ⁄ 4 | 2 ⁄ 7 | 0 ⁄ 9 6 3 |
| 4 | 0 ⁄ 4 | 0 ⁄ 8 | 1 ⁄ 2 | 1 ⁄ 6 | 2 ⁄ 0 | 2 ⁄ 4 | 2 ⁄ 8 | 3 ⁄ 2 | 3 ⁄ 6 | 1 ⁄ 6 8 4 |
| 5 | 0 ⁄ 5 | 1 ⁄ 0 | 1 ⁄ 5 | 2 ⁄ 0 | 2 ⁄ 5 | 3 ⁄ 0 | 3 ⁄ 5 | 4 ⁄ 0 | 4 ⁄ 5 | 2 ⁄ 5 10 5 |
| 6 | 0 ⁄ 6 | 1 ⁄ 2 | 1 ⁄ 8 | 2 ⁄ 4 | 3 ⁄ 0 | 3 ⁄ 6 | 4 ⁄ 2 | 4 ⁄ 8 | 5 ⁄ 4 | 3 ⁄ 6 12 6 |
| 7 | 0 ⁄ 7 | 1 ⁄ 4 | 2 ⁄ 1 | 2 ⁄ 8 | 3 ⁄ 5 | 4 ⁄ 2 | 4 ⁄ 9 | 5 ⁄ 6 | 6 ⁄ 3 | 4 ⁄ 9 14 7 |
| 8 | 0 ⁄ 8 | 1 ⁄ 6 | 2 ⁄ 4 | 3 ⁄ 2 | 4 ⁄ 0 | 4 ⁄ 8 | 5 ⁄ 6 | 6 ⁄ 4 | 7 ⁄ 2 | 6 ⁄ 4 16 8 |
| 9 | 0 ⁄ 9 | 1 ⁄ 8 | 2 ⁄ 7 | 3 ⁄ 6 | 4 ⁄ 5 | 5 ⁄ 4 | 6 ⁄ 3 | 7 ⁄ 2 | 8 ⁄ 1 | 8 ⁄ 1 18 9 |
Para encontrar la raíz cuadrada de 46785399, sus dígitos se agrupan en dos, comenzando por la derecha, por lo que se ve así:
- 46 78 53 99
- Nota: Un número con un número impar de dígitos como 85399 se agruparía como 08 53 99
El grupo más a la izquierda se elige primero, en este caso 46. Se elige el cuadrado más grande en el hueso de la raíz cuadrada menor que 46, que es el 36 de la sexta fila. El primer dígito de la solución es 6, ya que se eligió la sexta fila.
Luego, el número en la segunda columna de la sexta fila en el hueso de la raíz cuadrada, 12, se coloca en el tablero.
El valor de la primera columna de la sexta fila, 36, se resta de 46, lo que deja 10.
El siguiente grupo de dígitos, 78, se agrega junto al 10; esto deja el resto 1078.
En esta etapa, el tablero y los cálculos intermedios deberían verse así:
|
√46 78 53 99 = 6
− 36
10 78
|
Los números en cada fila se "leen", ignorando la segunda y tercera columnas del hueso de la raíz cuadrada; estos se registran. (Por ejemplo, la sexta fila se lee como: 0 ⁄ 6 1 ⁄ 2 3 ⁄ 6 → 756 ).
Como en la multiplicación mostrada anteriormente, los números se leen de derecha a izquierda y suman los números diagonales de arriba a derecha a izquierda-abajo ( 6 + 0 = 6 ; 3 + 2 = 5 ; 1 + 6 = 7 ).
Se encuentra el número más grande menor que el resto actual, 1078 (de la octava fila).
|
√46 78 53 99 = 68
− 36
10 78
− 10 24
54
|
Como antes, se agrega 8 para obtener el siguiente dígito de la raíz cuadrada y el valor de la octava fila, 1024, se resta del resto actual, 1078, para obtener 54. La segunda columna de la octava fila en el hueso de la raíz cuadrada , 16, se lee y el número se establece en el tablero de la siguiente manera.
El número actual en el tablero es 12. El primer dígito de 16 se agrega al 12, y el segundo dígito de 16 se agrega al resultado. Por lo tanto, la placa debe configurarse para:
- 12 + 1 = 13 → añadir 6 → 136
- Nota: Si la segunda columna del hueso de la raíz cuadrada tiene solo un dígito, este se agrega al número actual en la pizarra.
El tablero y los cálculos intermedios ahora se ven así.
|
√46 78 53 99 = 68
− 36
10 78
− 10 24
54 53
|
Una vez más, se encuentra la fila con el valor más grande menor que el resto parcial actual, 5453. Esta vez, es la tercera fila con 4089.
|
√46 78 53 99 = 683
− 36
10 78
− 10 24
54 53
− 40 89
13 64
|
El siguiente dígito de la raíz cuadrada es 3. Se repiten los mismos pasos que antes y se resta 4089 del resto actual, 5453, para obtener 1364 como resto siguiente. Cuando se reorganiza el tablero, la segunda columna del hueso de la raíz cuadrada es 6, un solo dígito. Por lo tanto, se agrega 6 al número actual en el tablero, 136, para dejar 1366 en el tablero.
- 136 → añadir 6 → 1366
|
√46 78 53 99 = 683
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
|
El proceso se repite nuevamente. Ahora, el valor más grande en el tablero menor que el resto actual, 136499, es 123021 de la novena fila.
A menudo, no es necesario encontrar el valor de cada fila para obtener la respuesta. La fila que tiene la respuesta se puede adivinar mirando el número de los primeros huesos y comparándolo con los primeros dígitos del resto. Pero los diagramas muestran el valor de todas las filas para que sea comprensible.
Se agrega 9 al resultado y 123021 se resta del resto actual.
|
√46 78 53 99 = 6839
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
− 12 30 21
1 34 78
|
Si se han usado todos los dígitos y queda un resto, entonces la parte entera está resuelta, pero aún es necesario encontrar un bit fraccionario.
Si se resuelve la parte entera, el resultado actual al cuadrado ( 6839 2 = 46771921 ) debe ser el cuadrado perfecto más grande menor que 46785899.
Esta idea se usa más adelante para comprender cómo funciona la técnica, pero se pueden generar más dígitos.
Similar a encontrar la porción fraccionaria en la división larga , se agregan dos ceros al resto para obtener el nuevo resto 1347800. La segunda columna de la novena fila del hueso de la raíz cuadrada es 18 y el número actual en el tablero es 1366.
- 1366 + 1 → 1367 → anexar 8 → 13678
se calcula para establecer 13678 en la placa.
El tablero y los cálculos intermedios ahora se ven así.
|
√46 78 53 99.00 = 6839.
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
− 12 30 21
1 34 78 00
|
La novena fila con 1231101 es el valor más grande menor que el resto, por lo que el primer dígito de la parte fraccionaria de la raíz cuadrada es 9.
|
√46 78 53 99.00 = 6839.9
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
− 12 30 21
1 34 78 00
− 1 23 11 01
11 66 99
|
El valor de la novena fila se resta del resto y se agregan algunos ceros más para obtener el nuevo resto 11669900. La segunda columna de la novena fila es 18 con 13678 en el tablero, entonces
- 13678 + 1 → 13679 → anexar 8 → 136798
se calcula para establecer 136798 en la placa.
|
√46 78 53 99.00 00 = 6839.9
− 36
10 78
− 10 24
54 53
− 40 89
13 64 99
− 12 30 21
1 34 78 00
− 1 23 11 01
11 66 99 00
|
Los pasos se pueden continuar para encontrar tantos dígitos necesarios y si se logra la precisión necesaria. Si el resto se convierte en cero, esto significa que se encontró la raíz cuadrada exacta.
Redondeando
Habiendo encontrado el número deseado de dígitos, es fácil determinar si es necesario redondear o no; es decir, cambiando el último dígito. No es necesario encontrar otro dígito para ver si es igual o mayor que 5. Se agrega 25 a la raíz y se compara con el resto; si es menor o igual que el resto, entonces el siguiente dígito será al menos cinco y es necesario redondear hacia arriba. En el ejemplo anterior, 6839925 es menor que 11669900, por lo que la raíz debe redondearse a 6840.0.
Para encontrar la raíz cuadrada de un número que no es un número entero, digamos 54782.917, todo es igual, excepto que los dígitos a la izquierda y a la derecha del punto decimal se agrupan en dos.
Entonces 54782.917 se agruparía como
- 05 47 82,91 70
Luego, la raíz cuadrada se puede encontrar usando el proceso mencionado anteriormente.
Modificación diagonal
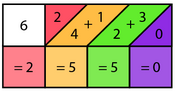
Durante el siglo XIX, los huesos de Napier se transformaron para facilitar su lectura. Las varillas se hicieron con un ángulo de unos 65 ° para que los triángulos que debían agregarse quedaran alineados. En este caso, en cada cuadrado de la varilla la unidad está a la derecha y el diez (o el cero) a la izquierda.
Las varillas se hicieron de manera que las líneas verticales y horizontales fueran más visibles que la línea donde se tocaban las varillas, haciendo que los dos componentes de cada dígito del resultado fueran más fáciles de leer. Por lo tanto, en la imagen queda inmediatamente claro que:
- 987654321 × 5 = 4938271605
Gobernantes de Genaille-Lucas
En 1891, Henri Genaille inventó una variante de los huesos de Napier que se conoció como gobernantes Genaille-Lucas . Al representar el acarreo gráficamente, los resultados de problemas simples de multiplicación se pueden leer directamente, sin cálculos mentales intermedios.
El siguiente ejemplo calcula 52749 × 4 = 210996 .