Mecánica del movimiento de partículas planar - Mechanics of planar particle motion

Parte de una serie sobre
Mecanica clasica
${\ Displaystyle {\ textbf {F}} = {\ frac {d} {dt}} (m {\ textbf {v}})}$ Segunda ley del movimiento
Historia Cronología Libros de texto
Sucursales
Fundamentos
Formulaciones
Temas centrales
Rotación
Científicos
Portal de física  Categoría
v t mi

Este artículo describe una partícula en movimiento plano cuando se observa desde sistemas de referencia no inerciales . Los ejemplos más famosos de movimiento plano están relacionados con el movimiento de dos esferas que se atraen gravitacionalmente entre sí, y la generalización de este problema al movimiento planetario . Vea la fuerza centrífuga , el problema de dos cuerpos , la órbita y las leyes del movimiento planetario de Kepler . Esos problemas caen en el campo general de la dinámica analítica , la determinación de órbitas a partir de leyes de fuerza dadas. Este artículo se centra más en las cuestiones cinemáticas que rodean el movimiento plano, es decir, la determinación de las fuerzas necesarias para dar como resultado una determinada trayectoria dada la trayectoria de la partícula. Los resultados generales presentados aquí en fuerzas ficticias se aplican a las observaciones de una partícula en movimiento como se ve desde varios marcos no inerciales específicos, por ejemplo, un marco local (uno vinculado a la partícula en movimiento para que parezca estacionaria) y un marco co-rotativo (uno con un eje fijo pero ubicado arbitrariamente y una tasa de rotación que hace que la partícula parezca tener solo movimiento radial y movimiento azimutal cero ). Se introduce el enfoque lagrangiano de las fuerzas ficticias.

A diferencia de las fuerzas reales , como las fuerzas electromagnéticas , las fuerzas ficticias no se originan a partir de interacciones físicas entre objetos.

Análisis usando fuerzas ficticias

La aparición de fuerzas ficticias normalmente se asocia con el uso de un marco de referencia no inercial y su ausencia con el uso de un marco de referencia inercial . La conexión entre marcos inerciales y fuerzas ficticias (también llamadas fuerzas inerciales o pseudo-fuerzas ), se expresa, por ejemplo, por Arnol'd:

Las ecuaciones de movimiento en un sistema no inercial se diferencian de las ecuaciones en un sistema inercial por términos adicionales llamados fuerzas inerciales. Esto nos permite detectar experimentalmente la naturaleza no inercial de un sistema.

-  VI Arnol'd: Métodos matemáticos de la mecánica clásica, segunda edición, p. 129

Iro proporciona un enfoque ligeramente diferente sobre el tema:

Una fuerza adicional debida al movimiento relativo no uniforme de dos marcos de referencia se denomina pseudofuerza .

-  H Iro en Un enfoque moderno de la mecánica clásica p. 180

Las fuerzas ficticias no aparecen en las ecuaciones de movimiento en un marco de referencia inercial : en un marco inercial, el movimiento de un objeto se explica por las fuerzas reales impresas. Sin embargo, en un marco no inercial como un marco giratorio, la primera y la segunda leyes de Newton todavía se pueden utilizar para realizar predicciones físicas precisas siempre que se incluyan fuerzas ficticias junto con las fuerzas reales. Para resolver problemas de mecánica en marcos de referencia no inerciales, el consejo que se da en los libros de texto es tratar las fuerzas ficticias como fuerzas reales y pretender que estás en un marco inercial.

Trate las fuerzas ficticias como fuerzas reales y finja que está en un marco inercial.

-  Louis N. Hand, Mecánica analítica de Janet D. Finch , pág. 267

Cabe mencionar que "tratar las fuerzas ficticias como fuerzas reales" significa, en particular, que las fuerzas ficticias como se ven en un marco no inercial particular se transforman como vectores bajo transformaciones coordinadas realizadas dentro de ese marco, es decir, como fuerzas reales.

Objetos en movimiento y marcos de referencia de observación

A continuación, se observa que las coordenadas que varían en el tiempo se utilizan en marcos de referencia inerciales y no inerciales, por lo que el uso de coordenadas que varían en el tiempo no debe confundirse con un cambio de observador, sino que es solo un cambio de la elección de descripción del observador. . A continuación se detalla este punto y se citan algunas citas sobre el tema.

Marco de referencia y sistema de coordenadas

El término marco de referencia se utiliza a menudo en un sentido muy amplio, pero para la presente discusión su significado se limita a referirse a de un observador estado de movimiento , es decir, ya sea a un sistema inercial de referencia o un marco no inercial de referencia .

El término sistema de coordenadas se usa para diferenciar entre diferentes opciones posibles para un conjunto de variables para describir el movimiento, opciones disponibles para cualquier observador, independientemente de su estado de movimiento. Algunos ejemplos son las coordenadas cartesianas , las coordenadas polares y (más generalmente) las coordenadas curvilíneas .

Aquí hay dos citas que relacionan "estado de movimiento" y "sistema de coordenadas":

Primero introducimos la noción de marco de referencia , en sí mismo relacionado con la idea de observador : el marco de referencia es, en cierto sentido, el "espacio euclidiano llevado por el observador". Démosle una definición más matemática: ... el marco de referencia es ... el conjunto de todos los puntos en el espacio euclidiano con el movimiento del cuerpo rígido del observador. El bastidor, indicado , se dice que mover con el observador. ... las posiciones espaciales de las partículas están etiquetados con relación a un marco mediante el establecimiento de un sistema de coordenadas R con origen O . Se puede considerar que el conjunto de ejes correspondiente, que comparte el movimiento rígido del cuerpo del marco , da una realización física de . En un marco , las coordenadas se cambian de R a R ' realizando, en cada instante de tiempo, la misma transformación de coordenadas sobre las componentes de los objetos intrínsecos (vectores y tensores) introducidos para representar cantidades físicas en este marco .${\ Displaystyle {\ mathfrak {R}}}$${\ Displaystyle {\ mathfrak {R}}}$ ${\ Displaystyle {\ mathfrak {R}}}$${\ Displaystyle {\ mathfrak {R}}}$${\ Displaystyle {\ mathfrak {R}}}$

-  Jean Salençon, Stephen Lyle. (2001). Manual de Mecánica Continua: Conceptos Generales, Termoelasticidad p. 9

En los desarrollos tradicionales de la relatividad especial y general se ha acostumbrado a no distinguir entre dos ideas completamente distintas. La primera es la noción de un sistema de coordenadas, entendido simplemente como la asignación suave e invertible de cuatro números a eventos en vecindarios del espacio-tiempo. El segundo, el marco de referencia, se refiere a un sistema idealizado utilizado para asignar tales números ... Para evitar restricciones innecesarias, podemos divorciar este arreglo de las nociones métricas. ... De especial importancia para nuestros propósitos es que cada marco de referencia tiene un estado definido de movimiento en cada evento del espacio-tiempo ... Dentro del contexto de la relatividad especial y siempre que nos limitemos a marcos de referencia en movimiento inercial, entonces poco de La importancia depende de la diferencia entre un marco de referencia inercial y el sistema de coordenadas inercial que induce. Esta cómoda circunstancia cesa inmediatamente una vez que comenzamos a considerar marcos de referencia en movimiento no uniforme incluso dentro de la relatividad especial ... la noción de marco de referencia ha reaparecido como una estructura distinta de un sistema de coordenadas.

-  John D. Norton: Covarianza general y los fundamentos de la relatividad general: ocho décadas de disputa , Rep. Prog. Phys. , 56 , págs. 835-7.

Sistemas de coordenadas variables en el tiempo

En un sistema de coordenadas general, los vectores base para las coordenadas pueden variar en el tiempo en posiciones fijas, o pueden variar con la posición en momentos fijos, o ambos. Cabe señalar que los sistemas de coordenadas adjuntos tanto a los marcos inerciales como a los marcos no inerciales pueden tener vectores base que varían en el tiempo, el espacio o ambos, por ejemplo, la descripción de una trayectoria en coordenadas polares como se ve desde un marco inercial. o como se ve desde un marco giratorio. Una descripción de las observaciones que depende del tiempo no cambia el marco de referencia en el que se realizan y registran las observaciones.

Fuerzas ficticias en un sistema de coordenadas local

Figura 1: Sistema de coordenadas local para movimiento plano en una curva. Dos posiciones diferentes se muestran para distancias s y s + ds a lo largo de la curva. En cada posición s , el vector unitario u _n apunta a lo largo de la normal hacia afuera a la curva y el vector unitario u _t es tangencial a la trayectoria. El radio de curvatura de la trayectoria es ρ calculado a partir de la tasa de rotación de la tangente a la curva con respecto a la longitud del arco, y es el radio del círculo osculante en la posición s . El círculo unitario de la izquierda muestra la rotación de los vectores unitarios con s .

Al hablar de una partícula que se mueve en una órbita circular, en un marco de referencia inercial se pueden identificar las fuerzas centrípeta y tangencial. Entonces parece que no hay problema para cambiar de sombrero, cambiar de perspectiva y hablar sobre las fuerzas ficticias comúnmente llamadas fuerza centrífuga y de Euler . Pero lo que subyace a este cambio en el vocabulario es un cambio del marco de referencia observacional desde el marco inercial donde comenzamos, donde las fuerzas centrípetas y tangenciales tienen sentido, a un marco de referencia giratorio donde la partícula parece inmóvil y ficticia centrífuga y las fuerzas de Euler tienen que ser puesto en juego. Ese cambio es inconsciente, pero real.

Supongamos que nos sentamos sobre una partícula en movimiento plano general (no solo una órbita circular). ¿Qué análisis subyace en un cambio de sombreros para introducir fuerzas centrífugas y de Euler ficticias?

Para explorar esa pregunta, comience en un marco de referencia inercial. Al utilizar un sistema de coordenadas comúnmente utilizado en el movimiento plano, el llamado sistema de coordenadas local , como se muestra en la Figura 1 , resulta fácil identificar fórmulas para la fuerza centrípeta hacia adentro normal a la trayectoria (en dirección opuesta a u _n en la Figura 1 ), y la fuerza tangencial paralela a la trayectoria (en la dirección u _t ), como se muestra a continuación.

Para introducir los vectores unitarios del sistema de coordenadas local que se muestra en la Figura 1 , un enfoque es comenzar en coordenadas cartesianas en un marco inercial y describir las coordenadas locales en términos de estas coordenadas cartesianas. En la Figura 1 , la longitud del arco s es la distancia que la partícula ha viajado a lo largo de su trayectoria en el tiempo t . La trayectoria r ( t ) con componentes x ( t ), y ( t ) en coordenadas cartesianas se describe usando la longitud del arco s ( t ) como:

${\ Displaystyle \ mathbf {r} (s) = \ left [x (s), \ y (s) \ right] \.}$

La longitud del arco s (t) mide la distancia a lo largo del rastro del skywriter. Imagen de NASA ASRS

Una forma de ver el uso de s es pensar en el camino de la partícula como si estuviera sentada en el espacio, como el rastro dejado por un escritor del cielo , independientemente del tiempo. Cualquier posición en este camino se describe indicando su distancia s desde algún punto de inicio en el camino. Entonces, un desplazamiento incremental a lo largo de la trayectoria ds se describe mediante:

${\ Displaystyle d \ mathbf {r} (s) = \ left [dx (s), \ dy (s) \ right] = \ left [x '(s), \ y' (s) \ right] ds \ ,}$

donde los números primos se introducen para denotar derivadas con respecto a s . La magnitud de este desplazamiento es ds , lo que muestra que:

${\ Displaystyle \ left [x '(s) ^ {2} + y' (s) ^ {2} \ right] = 1 \.}$    (Ecuación 1)

Este desplazamiento es necesariamente tangente a la curva en s , lo que muestra que el vector unitario tangente a la curva es:

${\ Displaystyle \ mathbf {u} _ {t} (s) = \ left [x '(s), \ y' (s) \ right] \,}$

mientras que el vector unitario exterior normal a la curva es

${\ Displaystyle \ mathbf {u} _ {n} (s) = \ left [y '(s), \ -x' (s) \ right] \,}$

La ortogonalidad se puede verificar mostrando que el producto escalar del vector es cero. La magnitud unitaria de estos vectores es una consecuencia de la ecuación. 1 .

Como acotación al margen, observe que el uso de vectores unitarios que no están alineados a lo largo de los ejes xy cartesianos no significa que ya no estamos en un marco inercial. Todo lo que significa es que estamos usando vectores unitarios que varían con s para describir la trayectoria, pero aún observamos el movimiento desde el marco inercial.

Usando el vector tangente, el ángulo de la tangente a la curva, digamos θ, viene dado por:

${\ Displaystyle \ sin \ theta = {\ frac {y '(s)} {\ sqrt {x' (s) ^ {2} + y '(s) ^ {2}}}} = y' (s) \;}$   y   ${\ Displaystyle \ cos \ theta = {\ frac {x '(s)} {\ sqrt {x' (s) ^ {2} + y '(s) ^ {2}}}} = x' (s) \.}$

El radio de curvatura se introduce de forma completamente formal (sin necesidad de interpretación geométrica) como:

${\ Displaystyle {\ frac {1} {\ rho}} = {\ frac {d \ theta} {ds}} \.}$

La derivada de θ se puede encontrar a partir de la de sin θ:

${\ Displaystyle {\ frac {d \ sin \ theta} {ds}} = \ cos \ theta {\ frac {d \ theta} {ds}} = {\ frac {1} {\ rho}} \ cos \ theta \}$

${\ Displaystyle = {\ frac {1} {\ rho}} x '(s) \.}$

Ahora:

${\ Displaystyle {\ frac {d \ sin \ theta} {ds}} = {\ frac {d} {ds}} {\ frac {y '(s)} {\ sqrt {x' (s) ^ {2 } + y '(s) ^ {2}}}}}$  ${\ Displaystyle = {\ frac {y '' (s) x '(s) ^ {2} -y' (s) x '(s) x' '(s)} {\ left (x' (s) ^ {2} + y '(s) ^ {2} \ right) ^ {3/2}}} \,}$

en el que el denominador es la unidad según Eq. 1 . Con esta fórmula para la derivada del seno, el radio de curvatura se convierte en:

${\ Displaystyle {\ frac {d \ theta} {ds}} = {\ frac {1} {\ rho}} = y '' (s) x '(s) -y' (s) x '' (s ) \}$ ${\ Displaystyle = {\ frac {y '' (s)} {x '(s)}} = - {\ frac {x' '(s)} {y' (s)}} \,}$

donde la equivalencia de las formas proviene de la diferenciación de Eq. 1 :

${\ Displaystyle x '(s) x' '(s) + y' (s) y '' (s) = 0 \.}$

Habiendo establecido la descripción de cualquier posición en la ruta en términos de su valor asociado para s , y habiendo encontrado las propiedades de la ruta en términos de esta descripción, el movimiento de la partícula se introduce indicando la posición de la partícula en cualquier momento t como el valor correspondiente s (t) .

Usando los resultados anteriores para las propiedades de la ruta en términos de s , la aceleración en el marco de referencia inercial como se describe en términos de los componentes normal y tangencial a la ruta de la partícula se puede encontrar en términos de la función s ( t ) y su Varias derivadas en el tiempo (como antes, los números primos indican diferenciación con respecto a s ):

${\ Displaystyle \ mathbf {a} (s) = {\ frac {d} {dt}} \ mathbf {v} (s)}$  ${\ Displaystyle = {\ frac {d} {dt}} \ left [{\ frac {ds} {dt}} \ left (x '(s), \ y' (s) \ right) \ right] \}$

${\ Displaystyle = \ left ({\ frac {d ^ {2} s} {dt ^ {2}}} \ right) \ mathbf {u} _ {t} (s) + \ left ({\ frac {ds } {dt}} \ right) ^ {2} \ left (x '' (s), \ y '' (s) \ right)}$

${\ displaystyle = \ left ({\ frac {d ^ {2} s} {dt ^ {2}}} \ right) \ mathbf {u} _ {t} (s) - \ left ({\ frac {ds } {dt}} \ right) ^ {2} {\ frac {1} {\ rho}} \ mathbf {u} _ {n} (s) \,}$

como se puede verificar tomando el producto escalar con los vectores unitarios u _t ( s ) y u _n ( s ). Este resultado para la aceleración es el mismo que para el movimiento circular basado en el radio ρ. Usando este sistema de coordenadas en el marco inercial, es fácil identificar la fuerza normal a la trayectoria como la fuerza centrípeta y la paralela a la trayectoria como la fuerza tangencial.

A continuación, cambiamos los marcos de observación. Sentados sobre la partícula, adoptamos un marco no inercial donde la partícula está en reposo (velocidad cero). Este marco tiene un origen que cambia continuamente, que en el momento t es el centro de curvatura (el centro del círculo osculante en la Figura 1 ) de la trayectoria en el momento t , y cuya tasa de rotación es la tasa angular de movimiento de la partícula alrededor de ese origen en el tiempo t . Este marco no inercial también emplea vectores unitarios normales a la trayectoria y paralelos a ella.

La velocidad angular de este marco es la velocidad angular de la partícula alrededor del centro de curvatura en el tiempo t . La fuerza centrípeta del marco inercial se interpreta en el marco no inercial donde el cuerpo está en reposo como una fuerza necesaria para vencer la fuerza centrífuga. Asimismo, la fuerza que causa cualquier aceleración de la velocidad a lo largo de la trayectoria vista en el marco inercial se convierte en la fuerza necesaria para superar la fuerza de Euler en el marco no inercial donde la partícula está en reposo. Hay una fuerza de Coriolis cero en el marco, porque la partícula tiene velocidad cero en este marco. Para un piloto de un avión, por ejemplo, estas fuerzas ficticias son una cuestión de experiencia directa. Sin embargo, estas fuerzas ficticias no pueden relacionarse con un marco de referencia de observación simple que no sea la propia partícula, a menos que se encuentre en una trayectoria particularmente simple, como un círculo.

Dicho esto, desde un punto de vista cualitativo, la trayectoria de un avión se puede aproximar mediante un arco de círculo durante un tiempo limitado, y durante el tiempo limitado se aplica un radio de curvatura particular, las fuerzas centrífugas y de Euler pueden analizarse sobre la base de de movimiento circular con ese radio. Vea el artículo sobre cómo girar un avión .

A continuación, se analizan con más detalle los marcos de referencia que giran alrededor de un eje fijo.

Fuerzas ficticias en coordenadas polares

La descripción del movimiento de partículas a menudo es más simple en sistemas de coordenadas no cartesianos, por ejemplo, coordenadas polares. Cuando las ecuaciones de movimiento se expresan en términos de cualquier sistema de coordenadas curvilíneas, aparecen términos adicionales que representan cómo cambian los vectores base a medida que cambian las coordenadas. Estos términos surgen automáticamente al transformarse en coordenadas polares (o cilíndricas) y, por lo tanto, no son fuerzas ficticias , sino que son simplemente términos agregados en la aceleración en coordenadas polares.

Dos terminologias

En un tratamiento puramente matemático, independientemente del marco con el que esté asociado el sistema de coordenadas (inercial o no inercial), aparecen términos adicionales en la aceleración de una partícula observada cuando se utilizan coordenadas curvilíneas. Por ejemplo, en coordenadas polares, la aceleración viene dada por (ver más abajo para más detalles):

${\ displaystyle {\ boldsymbol {a}} = {\ frac {d {\ boldsymbol {v}}} {dt}} = {\ frac {d ^ {2} \ mathbf {r}} {dt ^ {2} }} = ({\ ddot {r}} - r {\ dot {\ theta}} ^ {2}) {\ hat {\ boldsymbol {r}}} + (r {\ ddot {\ theta}} + 2 {\ dot {r}} {\ dot {\ theta}}) {\ hat {\ boldsymbol {\ theta}}} \,}$

que contiene no solo derivadas de tiempo doble de las coordenadas, sino términos agregados. Este ejemplo emplea coordenadas polares, pero más generalmente los términos agregados dependen del sistema de coordenadas que se elija (es decir, polar, elíptico o lo que sea). A veces, estos términos dependientes del sistema de coordenadas también se denominan "fuerzas ficticias", introduciendo un segundo significado para "fuerzas ficticias", a pesar de que estos términos no tienen las propiedades de transformación vectorial que se esperan de las fuerzas. Por ejemplo, consulte Shankar y Hildebrand. De acuerdo con esta terminología, las fuerzas ficticias están determinadas en parte por el propio sistema de coordenadas, independientemente del marco al que esté unido, es decir, independientemente de si el sistema de coordenadas está unido a un marco de referencia inercial o no inercial. Por el contrario, las fuerzas ficticias definidas en términos del estado de movimiento del observador se desvanecen en marcos de referencia inerciales. Para distinguir estas dos terminologías, las fuerzas ficticias que se desvanecen en un marco de referencia inercial, las fuerzas inerciales de la mecánica newtoniana, se denominan en este artículo las fuerzas ficticias del "estado de movimiento" y las que se originan en la interpretación de las derivadas del tiempo. en particular, los sistemas de coordenadas se denominan fuerzas ficticias "coordinadas".

Suponiendo que está claro que el "estado de movimiento" y el "sistema de coordenadas" son diferentes , se deduce que la dependencia de la fuerza centrífuga (como en este artículo) del "estado de movimiento" y su independencia del "sistema de coordenadas", que contrasta con la versión "coordinada" con exactamente las dependencias opuestas, indica que dos ideas diferentes son referidas por la terminología "fuerza ficticia". El presente artículo enfatiza una de estas dos ideas ("estado de movimiento"), aunque también se describe la otra.

A continuación, se introducen las coordenadas polares para su uso en (primero) un marco de referencia inercial y luego (segundo) en un marco de referencia giratorio. Se señalan los dos usos diferentes del término "fuerza ficticia". Primero, sin embargo, sigue una breve digresión para explicar con más detalle cómo ha surgido la terminología de "coordenadas" para la fuerza ficticia.

Enfoque lagrangiano

Para motivar la introducción de fuerzas de inercia "coordinadas" por algo más que una referencia a la "conveniencia matemática", lo que sigue es una digresión para mostrar que estas fuerzas corresponden a lo que algunos autores denominan fuerzas ficticias "generalizadas" o "fuerzas de inercia generalizadas". Estas fuerzas se introducen a través del enfoque de la mecánica de Lagrange a la mecánica basado en la descripción de un sistema mediante coordenadas generalizadas, generalmente denotadas como { q _k }. El único requisito de estas coordenadas es que sean necesarias y suficientes para caracterizar de forma única el estado del sistema: no necesitan ser (aunque podrían ser) las coordenadas de las partículas en el sistema. En cambio, podrían ser los ángulos y extensiones de enlaces en un brazo robótico, por ejemplo. Si un sistema mecánico consta de N partículas y hay m condiciones cinemáticas independientes impuestas, es posible caracterizar el sistema de manera única por n = 3 N - m coordenadas generalizadas independientes { q _k }.

En la mecánica clásica, la función de Lagrange se define como la energía cinética , , del sistema de menos su energía potencial , . En símbolos, ${\ Displaystyle T}$${\ Displaystyle U}$

${\ Displaystyle L = TU. \ quad}$

En las condiciones que se dan en la mecánica lagrangiana , si se conoce el lagrangiano de un sistema, entonces las ecuaciones de movimiento del sistema pueden obtenerse mediante una sustitución directa de la expresión del lagrangiano en la ecuación de Euler-Lagrange , una familia particular de ecuaciones diferenciales parciales .

Aquí hay algunas definiciones:

Definición :

${\ displaystyle L ({\ boldsymbol {q}}, \ {\ boldsymbol {\ dot {q}}}, \ t) = TU}$

es la función de Lagrange o lagrangiana , q _i son las coordenadas generalizadas , son velocidades generalizadas , ${\ Displaystyle {\ dot {q_ {i}}}}$

${\ Displaystyle \ L parcial / \ parcial {\ dot {q_ {i}}}}$   son momentos generalizados ,

${\ Displaystyle \ parcial L / \ parcial q_ {i}}$   son fuerzas generalizadas ,

${\ Displaystyle {\ frac {d} {dt}} {\ frac {\ parcial L} {\ parcial {\ punto {q_ {i}}}}} - {\ frac {\ parcial L} {\ parcial q_ { i}}} = 0}$   son las ecuaciones de Lagrange .

No es el propósito aquí esbozar cómo funciona la mecánica lagrangiana. El lector interesado puede consultar otros artículos que explican este enfoque. Por el momento, el objetivo es simplemente mostrar que el enfoque lagrangiano puede conducir a "fuerzas ficticias generalizadas" que no desaparecen en marcos inerciales . Lo que es pertinente aquí es que, en el caso de una sola partícula, el enfoque lagrangiano puede organizarse para capturar exactamente las fuerzas ficticias "coordinadas" que se acaban de introducir.

Para continuar, considere una sola partícula e introduzca las coordenadas generalizadas como { q _k } = ( r, θ ). Entonces Hildebrand muestra en coordenadas polares con q _k = (r, θ) los "momentos generalizados" son:

${\ Displaystyle p_ {r} = m {\ dot {r}} \, \ p _ {\ theta} = mr ^ {2} {\ dot {\ theta}} \,}$

conduciendo, por ejemplo, a la fuerza generalizada:

${\ Displaystyle {\ frac {d} {dt}} p_ {r} = Q_ {r} + mr {\ dot {\ theta}} ^ {2} \,}$

con Q _r la fuerza radial impresa. La conexión entre las "fuerzas generalizadas" y las fuerzas newtonianas varía con la elección de coordenadas. Esta formulación lagrangiana introduce exactamente la forma "coordinada" de fuerzas ficticias mencionadas anteriormente que permite fuerzas "ficticias" (generalizadas) en marcos inerciales, por ejemplo, el término Lectura cuidadosa de Hildebrand muestra que no discute el papel de "marcos inerciales de referencia ", y de hecho, dice" [La] presencia o ausencia [de fuerzas de inercia] depende, no del problema particular en cuestión, sino del sistema de coordenadas elegido ". Presumiblemente, por sistema de coordenadas se entiende la elección de { q _k }. Más adelante dice: "Si las aceleraciones asociadas con coordenadas generalizadas son de interés principal (como suele ser el caso), los términos [no acelerados] pueden transferirse convenientemente a la derecha ... y considerarse como fuerzas de inercia adicionales (generalizadas). Tales fuerzas de inercia a menudo se dice que son del tipo Coriolis ". ${\ Displaystyle mr {\ dot {\ theta}} ^ {2} \.}$

En resumen, el énfasis de algunos autores en las coordenadas y sus derivadas y su introducción de fuerzas ficticias (generalizadas) que no desaparecen en marcos de referencia inerciales es una consecuencia del uso de coordenadas generalizadas en la mecánica lagrangiana . Por ejemplo, consulte McQuarrie Hildebrand y von Schwerin. A continuación se muestra un ejemplo de este uso empleado en el diseño de manipuladores robóticos:

En las ecuaciones de [Lagrange-Euler] anteriores, hay tres tipos de términos. El primero involucra la segunda derivada de las coordenadas generalizadas. El segundo es cuadrático en el que los coeficientes pueden depender . Estos se clasifican además en dos tipos. Los términos que implican un producto del tipo se denominan fuerzas centrífugas, mientras que los que implican un producto del tipo para i ≠ j se denominan fuerzas de Coriolis . El tercer tipo son funciones de solo y se denominan fuerzas gravitacionales .${\ Displaystyle \ mathbf {\ dot {q}}}$${\ Displaystyle \ mathbf {q}}$${\ Displaystyle {{\ dot {q}} _ {i}} ^ {2}}$${\ Displaystyle {\ dot {q}} _ {i} {\ dot {q}} _ {j}}$${\ Displaystyle \ mathbf {q}}$

-  Shuzhi S. Ge, Tong Heng Lee y Christopher John Harris: Control adaptativo de la red neuronal de manipuladores robóticos , págs. 47-48

Para un robot manipulador, las ecuaciones se pueden escribir en una forma usando los símbolos de Christoffel Γ _ijk (discutidos más adelante) como:

${\ Displaystyle \ sum _ {j = 1} ^ {n} \ M_ {ij} ({\ boldsymbol {q}}) {\ ddot {q}} _ {j} + \ sum _ {j, k = 1 } ^ {n} \ Gamma _ {ijk} {\ dot {q}} _ {j} {\ dot {q}} _ {k} + {\ frac {\ parcial V} {\ parcial q_ {i}} } = \ Upsilon _ {i} \; i = 1, ..., n \,}$

donde M es la "matriz de inercia del manipulador" y V es la energía potencial debida a la gravedad (por ejemplo), y son las fuerzas generalizadas sobre la articulación i . Los términos que involucran símbolos de Christoffel, por lo tanto, determinan los términos "centrífugo generalizado" y "Coriolis generalizado". ${\ Displaystyle \ Upsilon _ {i}}$

La introducción de fuerzas ficticias generalizadas a menudo se realiza sin notificación y sin especificar la palabra "generalizado". Este uso descuidado de la terminología conduce a una confusión sin fin porque estas fuerzas ficticias generalizadas , a diferencia de las fuerzas ficticias estándar del "estado de movimiento", no desaparecen en marcos de referencia inerciales.

Coordenadas polares en un marco de referencia inercial

El vector de posición r , siempre apunta radialmente desde el origen.

Vector de velocidad v , siempre tangente a la trayectoria del movimiento.

Vector de aceleración a , no paralelo al movimiento radial pero compensado por las aceleraciones angular y de Coriolis, ni tangente a la trayectoria pero compensado por las aceleraciones centrípeta y radial.

Vectores cinemáticos en coordenadas polares planas. Observe que la configuración no está restringida al espacio 2d, sino a un plano en cualquier dimensión superior.

A continuación, la aceleración de una partícula se deriva como se ve en un marco inercial usando coordenadas polares. No hay fuerzas ficticias de "estado de movimiento" en un marco inercial, por definición. Después de esa presentación, la terminología contrastante de fuerzas ficticias "coordinadas" se presenta y critica sobre la base del comportamiento de transformación no vectorial de estas "fuerzas".

En un marco inercial, sea ​​el vector de posición de una partícula en movimiento. Sus componentes cartesianos ( x , y ) son: ${\ Displaystyle \ mathbf {r}}$

${\ Displaystyle \ mathbf {r} = (r \ cos \ theta, \ r \ sin \ theta) \,}$

con coordenadas polares r y θ dependiendo del tiempo t .

Los vectores unitarios se definen en la dirección radialmente hacia afuera : ${\ Displaystyle \ mathbf {r}}$

${\ displaystyle {\ hat {\ boldsymbol {r}}} = {\ frac {\ parcial \ mathbf {r}} {\ parcial r}} = (\ cos \ theta, \ \ sin \ theta)}$

y en la dirección perpendicular a : ${\ Displaystyle \ mathbf {r}}$

${\ Displaystyle {\ hat {\ boldsymbol {\ theta}}} = {\ frac {\ parcial ^ {2} {\ mathbf {r}}} {\ parcial r \, \ parcial \ theta}} = (- \ pecado \ theta \, \ cos \ theta) \.}$

Estos vectores unitarios varían en dirección con el tiempo:

${\ Displaystyle {\ frac {d} {dt}} {\ hat {\ boldsymbol {r}}} = (- \ sin \ theta, \ \ cos \ theta) {\ frac {d \ theta} {dt}} = {\ frac {d \ theta} {dt}} {\ hat {\ boldsymbol {\ theta}}},}$

y:

${\ Displaystyle {\ frac {d} {dt}} {\ hat {\ boldsymbol {\ theta}}} = (- \ cos \ theta, \ - \ sin \ theta) {\ frac {d \ theta} {dt }} = - {\ frac {d \ theta} {dt}} {\ hat {\ boldsymbol {r}}}.}$

Usando estas derivadas, la primera y segunda derivadas de posición son:

${\ displaystyle {\ boldsymbol {v}} = {\ frac {d \ mathbf {r}} {dt}} = {\ dot {r}} {\ hat {\ boldsymbol {r}}} + r {\ dot {\ theta}} {\ hat {\ boldsymbol {\ theta}}},}$

${\ displaystyle {\ boldsymbol {a}} = {\ frac {d {\ boldsymbol {v}}} {dt}} = {\ frac {d ^ {2} \ mathbf {r}} {dt ^ {2} }} = ({\ ddot {r}} - r {\ dot {\ theta}} ^ {2}) {\ hat {\ boldsymbol {r}}} + (r {\ ddot {\ theta}} + 2 {\ dot {r}} {\ dot {\ theta}}) {\ hat {\ boldsymbol {\ theta}}} \,}$

donde los puntos sobremarcados indican diferenciación de tiempo. Con esta forma para la aceleración , en un marco de referencia inercial, la segunda ley de Newton expresada en coordenadas polares es: ${\ displaystyle {\ boldsymbol {a}}}$

${\ displaystyle {\ boldsymbol {F}} = m {\ boldsymbol {a}} = m ({\ ddot {r}} - r {\ dot {\ theta}} ^ {2}) {\ hat {\ boldsymbol {r}}} + m (r {\ ddot {\ theta}} + 2 {\ dot {r}} {\ dot {\ theta}}) {\ hat {\ boldsymbol {\ theta}}} \,}$

donde F es la fuerza real neta sobre la partícula. No aparecen fuerzas ficticias porque todas las fuerzas ficticias son cero por definición en un marco inercial.

Sin embargo, desde un punto de vista matemático, a veces es útil colocar solo las derivadas de segundo orden en el lado derecho de esta ecuación; es decir, escribimos la ecuación anterior reordenando los términos como:

${\ Displaystyle {\ boldsymbol {F}} + mr {\ dot {\ theta}} ^ {2} {\ hat {\ mathbf {r}}} - m2 {\ dot {r}} {\ dot {\ theta }} {\ hat {\ boldsymbol {\ theta}}} = m {\ tilde {\ boldsymbol {a}}} = m {\ ddot {r}} {\ hat {\ boldsymbol {r}}} + mr { \ ddot {\ theta}} {\ hat {\ boldsymbol {\ theta}}} \,}$

donde se introduce una versión de "coordenadas" de la "aceleración":

${\ displaystyle {\ tilde {\ boldsymbol {a}}} = {\ ddot {r}} {\ hat {\ boldsymbol {r}}} + r {\ ddot {\ theta}} {\ hat {\ boldsymbol { \ theta}}} \,}$

que consta únicamente de derivadas temporales de segundo orden de las coordenadas r y θ. Los términos trasladados al lado de la fuerza de la ecuación ahora se tratan como "fuerzas ficticias" adicionales y, de manera confusa, las fuerzas resultantes también se denominan fuerza "centrífuga" y "Coriolis".

Estas "fuerzas" recién definidas son distintas de cero en un marco inercial , por lo que ciertamente no son las mismas que las fuerzas ficticias previamente identificadas que son cero en un marco inercial y diferentes de cero solo en un marco no inercial. En este artículo, estas fuerzas recién definidas se denominan fuerza centrífuga "coordinada" y fuerza de Coriolis "coordinada" para separarlas de las fuerzas del "estado de movimiento".

Figura 2: Dos sistemas de coordenadas que se diferencian por un desplazamiento de origen. El movimiento radial con velocidad constante v en un cuadro no es radial en el otro cuadro. Tasa angular , pero ${\ Displaystyle {\ dot {\ theta}} = 0}$${\ Displaystyle {\ dot {\ theta}} '\ neq 0 \.}$

Cambio de origen

Aquí hay una ilustración que muestra que el llamado "término centrífugo" no se transforma como una fuerza verdadera, poniendo cualquier referencia a este término no solo como un "término", sino como una fuerza centrífuga , bajo una luz dudosa. Suponga que en el marco S una partícula se aleja radialmente del origen a una velocidad constante. Vea la Figura 2. La fuerza sobre la partícula es cero según la primera ley de Newton. Ahora miramos lo mismo del cuadro S ' , que es el mismo, pero desplazado en origen. En S ', la partícula todavía está en movimiento en línea recta a velocidad constante, por lo que nuevamente la fuerza es cero. ${\ Displaystyle r {\ dot {\ theta}} ^ {2}}$

¿Qué pasa si usamos coordenadas polares en los dos cuadros? En el cuadro S, el movimiento radial es constante y no hay movimiento angular. Por tanto, la aceleración es:

${\ displaystyle {\ boldsymbol {a}} = \ left ({\ ddot {r}} - r {\ dot {\ theta}} ^ {2} \ right) {\ hat {\ boldsymbol {r}}} + \ left (r {\ ddot {\ theta}} + 2 {\ dot {r}} {\ dot {\ theta}} \ right) {\ hat {\ boldsymbol {\ theta}}} = 0 \,}$

y cada término individualmente es cero porque y . No hay fuerza, incluyendo sin "fuerza" en el marco S . En el cuadro S ' , sin embargo, tenemos: ${\ displaystyle {\ dot {\ theta}} = 0, \ {\ ddot {\ theta}} = 0}$${\ Displaystyle {\ ddot {r}} = 0 \}$${\ Displaystyle r {\ dot {\ theta}} ^ {2}}$

${\ displaystyle {\ boldsymbol {a}} '= \ left ({\ ddot {r}}' - r '{\ dot {\ theta}}' ^ {2} \ right) {\ hat {\ boldsymbol {r }}} '+ \ left (r' {\ ddot {\ theta}} '+ 2 {\ dot {r}}' {\ dot {\ theta}} '\ right) {\ hat {\ boldsymbol {\ theta }}} '\}$

En este caso, el término azimutal es cero, siendo la tasa de cambio del momento angular. Sin embargo, para obtener una aceleración cero en la dirección radial, necesitamos:

${\ Displaystyle {\ ddot {r}} '= r' {\ dot {\ theta}} '^ {2} \.}$

El lado derecho es distinto de cero, en la medida en que ni ni es cero. Es decir, no podemos obtener fuerza cero (cero ) si solo la retenemos como aceleración; necesitamos ambos términos. ${\ Displaystyle r '\}$${\ Displaystyle {\ dot {\ theta}} '}$${\ displaystyle {\ boldsymbol {a}} '\}$${\ Displaystyle {\ ddot {r}} '}$

A pesar de los hechos anteriores, supongamos que adoptamos coordenadas polares y deseamos decir que es "fuerza centrífuga", y reinterpretarlo como "aceleración" (sin detenernos en ninguna posible justificación). ¿Cómo le va a esta decisión cuando consideramos que una formulación adecuada de la física es independiente de la geometría y las coordenadas? Consulte el artículo sobre covarianza general . Para intentar formar una expresión covariante, esta llamada "fuerza" centrífuga se puede poner en notación vectorial como: ${\ Displaystyle r {\ dot {\ theta}} ^ {2}}$${\ Displaystyle {\ ddot {r}}}$

${\ displaystyle {\ boldsymbol {F _ {\ dot {\ theta}}}} = - {\ boldsymbol {\ omega \ times}} \ left ({\ boldsymbol {\ omega \ times r}} \ right) \,}$

con:

${\ displaystyle {\ boldsymbol {\ omega}} = {\ dot {\ theta}} {\ boldsymbol {\ hat {k}}} \,}$

y un vector unitario normal al plano de movimiento. Desafortunadamente, aunque esta expresión se ve formalmente como un vector, cuando un observador cambia de origen, el valor de los cambios (ver Figura 2), por lo que los observadores en el mismo marco de referencia parados en diferentes esquinas de las calles ven diferentes "fuerzas" a pesar de que los eventos reales los testigos son idénticos. ¿Cómo puede una fuerza física (ya sea ficticia o real) ser cero en un cuadro S , pero no cero en otro cuadro S ' idéntico, pero a unos pocos pies de distancia? Incluso para exactamente el mismo comportamiento de partículas, la expresión es diferente en cada marco de referencia, incluso para distinciones muy triviales entre marcos. En resumen, si lo tomamos como "fuerza centrífuga", no tiene un significado universal: no es físico . ${\ displaystyle {\ boldsymbol {\ hat {k}}}}$${\ Displaystyle {\ dot {\ theta}}}$${\ Displaystyle r {\ dot {\ theta}} ^ {2}}$${\ Displaystyle r {\ dot {\ theta}} ^ {2}}$

Más allá de este problema, la fuerza neta real impresa es cero. (No hay una fuerza real impresa en un movimiento en línea recta a velocidad constante). Si adoptamos coordenadas polares, y deseamos decir que es "fuerza centrífuga", y reinterpretarlo como "aceleración", la rareza resulta en el cuadro S ' que el movimiento en línea recta a velocidad constante requiere una fuerza neta en coordenadas polares, pero no en Coordenadas cartesianas. Por otra parte, esta perplejidad se aplica en el marco S ' , pero no en el marco S . ${\ Displaystyle r {\ dot {\ theta}} ^ {2}}$${\ Displaystyle {\ ddot {r}}}$

Lo absurdo del comportamiento de indica que hay que decir que no es fuerza centrífuga , sino simplemente uno de los dos términos de la aceleración. Esta visión, de que la aceleración se compone de dos términos, es independiente del marco: no hay fuerza centrífuga en todos y cada uno de los marcos inerciales. También es independiente del sistema de coordenadas: podemos usar cartesiano, polar o cualquier otro sistema curvilíneo: todos producen cero. ${\ Displaystyle r {\ dot {\ theta}} ^ {2}}$${\ Displaystyle r {\ dot {\ theta}} ^ {2}}$

Aparte de los argumentos físicos anteriores, por supuesto, la derivación anterior, basada en la aplicación de las reglas matemáticas de diferenciación, muestra que la aceleración radial de hecho consta de los dos términos . ${\ Displaystyle {\ ddot {r}} - r {\ dot {\ theta}} ^ {2}}$

Dicho esto, la siguiente subsección muestra que existe una conexión entre estos términos centrífugos y de Coriolis y las fuerzas ficticias que pertenecen a un marco de referencia giratorio particular (a diferencia de un marco inercial).

Figura 3: sistema de referencia inercial S y no inercial instantáneo de rotación conjunta marco de referencia S' . El marco de co-rotación gira a una tasa angular Ω igual a la tasa de rotación de la partícula alrededor del origen de S ' en el momento particular t . La partícula está ubicada en la posición del vector r (t) y los vectores unitarios se muestran en la dirección radial a la partícula desde el origen, y también en la dirección del ángulo creciente θ normal a la dirección radial. Estos vectores unitarios no necesitan estar relacionados con la tangente y la normal a la trayectoria. Además, la distancia radial r no necesita estar relacionada con el radio de curvatura del camino.

Marco co-giratorio

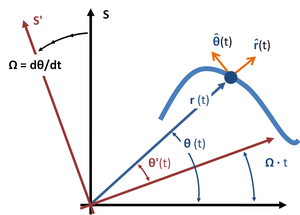
En el caso del movimiento plano de una partícula, los términos de "coordenada" centrífuga y de aceleración de Coriolis que se encuentran arriba como distintos de cero en un marco inercial pueden demostrarse que son los negativos de los términos de "estado de movimiento" centrífugo y de Coriolis. que aparecen en un marco co-rotativo no inercial muy particular (ver siguiente subsección). Ver figura 3 . Para definir un marco de co-rotación, primero se selecciona un origen a partir del cual se define la distancia r (t) a la partícula. Se establece un eje de rotación perpendicular al plano de movimiento de la partícula y que pasa por este origen. Luego, en el momento t seleccionado , se hace que la tasa de rotación del marco co-rotativo Ω coincida con la tasa de rotación de la partícula alrededor de este eje, dθ / dt . El marco de co-rotación se aplica solo por un momento y debe ser re-seleccionado continuamente a medida que la partícula se mueve. Para obtener más detalles, consulte Coordenadas polares, términos centrífugos y Coriolis .

Coordenadas polares en un marco de referencia giratorio

A continuación, se utiliza el mismo enfoque para encontrar las fuerzas ficticias de un marco giratorio (no inercial). Por ejemplo, si se adopta un sistema de coordenadas polares giratorias para su uso en un marco de observación giratorio, ambos girando a la misma velocidad constante en sentido antihorario Ω, encontramos las ecuaciones de movimiento en este marco de la siguiente manera: la coordenada radial en el marco giratorio es tomado como r , pero el ángulo θ 'en el marco giratorio cambia con el tiempo:

${\ Displaystyle \ theta '= \ theta - \ Omega t \.}$

Como consecuencia,

${\ Displaystyle {\ dot {\ theta}} '= {\ dot {\ theta}} - \ Omega \.}$

Conectando este resultado a la aceleración usando los vectores unitarios de la sección anterior:

${\ Displaystyle {\ frac {d ^ {2} \ mathbf {r}} {dt ^ {2}}} = \ left [{\ ddot {r}} - r \ left ({\ dot {\ theta}} '+ \ Omega \ right) ^ {2} \ right] {\ hat {\ mathbf {r}}} + \ left [r {\ ddot {\ theta}}' + 2 {\ dot {r}} \ left ({\ dot {\ theta}} '+ \ Omega \ right) \ right] {\ hat {\ boldsymbol {\ theta}}}}$

${\ Displaystyle = ({\ ddot {r}} - r {\ dot {\ theta}} '^ {2}) {\ hat {\ mathbf {r}}} + (r {\ ddot {\ theta}} '+2 {\ dot {r}} {\ dot {\ theta}}') {\ hat {\ boldsymbol {\ theta}}} - \ left (2r \ Omega {\ dot {\ theta}} '+ r \ Omega ^ {2} \ right) {\ hat {\ mathbf {r}}} + \ left (2 {\ dot {r}} \ Omega \ right) {\ hat {\ boldsymbol {\ theta}}} \ .}$

Los dos términos iniciales tienen la misma forma que los del marco inercial, y son los únicos términos si el marco no gira, es decir, si Ω = 0. Sin embargo, en este marco giratorio tenemos los términos adicionales:

${\ Displaystyle - \ left (2r \ Omega {\ dot {\ theta}} '+ r \ Omega ^ {2} \ right) {\ hat {\ mathbf {r}}} + \ left (2 {\ dot { r}} \ Omega \ right) {\ hat {\ boldsymbol {\ theta}}}}$

El término radial Ω ² r es la fuerza centrífuga por unidad de masa debido a la rotación del sistema a una tasa Ω y el término radial es la componente radial de la fuerza de Coriolis por unidad de masa, donde es la componente tangencial de la velocidad de la partícula como se ve en la marco giratorio. El término es el llamado componente azimutal de la fuerza de Coriolis por unidad de masa. De hecho, estos términos adicionales se pueden usar para medir Ω y proporcionar una prueba para ver si el marco está girando o no, tal como se explica en el ejemplo de esferas idénticas en rotación . Si el observador puede describir el movimiento de la partícula utilizando las leyes del movimiento de Newton sin estos términos dependientes de Ω, el observador se encuentra en un marco de referencia inercial donde Ω = 0. ${\ Displaystyle 2r \ Omega {\ dot {\ theta}} '}$${\ Displaystyle r {\ dot {\ theta}} '}$${\ Displaystyle - \ left (2 {\ dot {r}} \ Omega \ right) {\ hat {\ boldsymbol {\ theta}}}}$

Estos "términos adicionales" en la aceleración de la partícula son las fuerzas ficticias del "estado de movimiento" para este marco giratorio, las fuerzas introducidas por la rotación del marco a una tasa angular Ω.

En este marco giratorio, ¿cuáles son las fuerzas ficticias "coordinadas"? Como antes, suponga que elegimos poner solo las derivadas de tiempo de segundo orden en el lado derecho de la ley de Newton:

${\ Displaystyle {\ boldsymbol {F}} + mr {\ dot {\ theta}} '^ {2} {\ hat {\ mathbf {r}}} - m2 {\ dot {r}} {\ dot {\ theta}} '{\ hat {\ boldsymbol {\ theta}}} + m \ left (2r \ Omega {\ dot {\ theta}}' + r \ Omega ^ {2} \ right) {\ hat {\ mathbf {r}}} - m \ left (2 {\ dot {r}} \ Omega \ right) {\ hat {\ boldsymbol {\ theta}}}}$ ${\ displaystyle = m {\ ddot {r}} {\ hat {\ mathbf {r}}} + mr {\ ddot {\ theta}} '\ {\ hat {\ boldsymbol {\ theta}}}}$ ${\ displaystyle = m {\ tilde {\ boldsymbol {a}}}}$

Si elegimos por conveniencia tratar como una de las llamadas "aceleraciones", entonces los términos se agregan a la llamada "fuerza ficticia", que no son fuerzas ficticias en "estado de movimiento", sino que en realidad son componentes de la fuerza. que persisten incluso cuando Ω = 0, es decir, persisten incluso en un marco de referencia inercial. Debido a que se agregan estos términos adicionales, la fuerza ficticia "coordinada" no es lo mismo que la fuerza ficticia del "estado de movimiento". Debido a estos términos adicionales, la fuerza ficticia "coordinada" no es cero incluso en un marco de referencia inercial. ${\ Displaystyle {\ tilde {\ boldsymbol {a}}}}$${\ Displaystyle (mr {\ dot {\ theta}} '^ {2} {\ hat {\ mathbf {r}}} - m2 {\ dot {r}} {\ dot {\ theta}}' {\ hat {\ boldsymbol {\ theta}}})}$

Más sobre el marco co-rotativo

Observe, sin embargo, el caso de un marco giratorio que tiene la misma tasa angular que la partícula, de modo que Ω = dθ / dt en algún momento particular (es decir, las coordenadas polares se establecen en la coordenada instantánea, no inercial). -marco giratorio de la Figura 3 ). En este caso, en este momento, dθ '/ dt = 0 . En este marco no inercial co-rotante en este momento las fuerzas ficticias "coordinadas" son solo las debidas al movimiento del marco, es decir, son las mismas que las fuerzas ficticias del "estado de movimiento", como se discutió en las observaciones sobre el marco co-rotativo de la Figura 3 en la sección anterior.

Fuerzas ficticias en coordenadas curvilíneas

Figura 4: Superficies de coordenadas, líneas de coordenadas y ejes de coordenadas de coordenadas curvilíneas generales.

Para citar a Bullo y Lewis: "Sólo en circunstancias excepcionales se puede describir la configuración del sistema lagrangiano mediante un vector en un espacio vectorial. En el entorno matemático natural, el espacio de configuración del sistema se describe vagamente como un espacio curvo, o más exactamente como un colector diferenciable ".

En lugar de coordenadas cartesianas , cuando las ecuaciones de movimiento se expresan en un sistema de coordenadas curvilíneas , los símbolos de Christoffel aparecen en la aceleración de una partícula expresada en este sistema de coordenadas, como se describe a continuación con más detalle. Considere la descripción del movimiento de una partícula desde el punto de vista de un marco de referencia inercial en coordenadas curvilíneas. Supongamos que la posición de un punto P en coordenadas cartesianas es ( x , y , z ) y en coordenadas curvilíneas es ( q ₁ , q ₂ . Q ₃ ). Entonces existen funciones que relacionan estas descripciones:

${\ Displaystyle x = x (q_ {1}, \ q_ {2}, \ q_ {3}) \;}$ ${\ Displaystyle \ q_ {1} = q_ {1} (x, \ y, \ z) \,}$

Etcétera. (El número de dimensiones puede ser mayor que tres). Un aspecto importante de tales sistemas de coordenadas es el elemento de la longitud del arco que permite determinar las distancias. Si las coordenadas curvilíneas forman un sistema de coordenadas ortogonales , el elemento de longitud de arco ds se expresa como:

${\ Displaystyle ds ^ {2} = \ sum _ {k = 1} ^ {d} \ left (h_ {k} \ right) ^ {2} \ left (dq_ {k} \ right) ^ {2} \ ,}$

donde las cantidades h _k se denominan factores de escala . Un cambio dq _k en q _k provoca un desplazamiento h _k dq _{k a lo} largo de la línea de coordenadas para q _k . En un punto P , colocamos los vectores unitarios e _k cada tangente a una línea de coordenadas de una variable q _k . Entonces, cualquier vector puede expresarse en términos de estos vectores base, por ejemplo, a partir de un marco de referencia inercial, el vector de posición de una partícula en movimiento r ubicada en el tiempo t en la posición P se convierte en:

${\ displaystyle {\ boldsymbol {r}} = \ sum _ {k = 1} ^ {d} q_ {k} \ {\ boldsymbol {e_ {k}}} \,}$

donde q _k es el vector de producto de punto de r y e _k . La velocidad v de una partícula en P , se puede expresar en P como:

${\ displaystyle {\ boldsymbol {v}} = \ sum _ {k = 1} ^ {d} v_ {k} \ {\ boldsymbol {e_ {k}}} \,}$

${\ displaystyle = {\ frac {d} {dt}} {\ boldsymbol {r}} = \ sum _ {k = 1} ^ {d} {\ dot {q}} _ {k} \ {\ boldsymbol { e_ {k}}} + \ sum _ {k = 1} ^ {d} q_ {k} \ {\ dot {\ boldsymbol {e_ {k}}}} \,}$

donde v _k es el producto escalar del vector de v y e _k , y los puntos superiores indican diferenciación en el tiempo. Las derivadas de tiempo de los vectores base se pueden expresar en términos de los factores de escala introducidos anteriormente. por ejemplo:

${\ displaystyle {\ frac {\ parcial} {\ parcial q_ {2}}} {\ boldsymbol {e_ {1}}} = - {\ boldsymbol {e}} _ {2} {\ frac {1} {h_ {2}}} {\ frac {\ parcial h_ {1}} {\ parcial q_ {2}}} - {\ boldsymbol {e}} _ {3} {\ frac {1} {h_ {3}}} {\ frac {\ parcial h_ {1}} {\ parcial q_ {3}}} \,}$  o, en general ${\ Displaystyle {\ frac {\ parcial {\ boldsymbol {e_ {j}}}} {\ parcial q_ {k}}} = \ sum _ {n = 1} ^ {d} {\ Gamma ^ {n}} _ {kj} {\ boldsymbol {e_ {n}}} \,}$

en el que los coeficientes de los vectores unitarios son los símbolos de Christoffel para el sistema de coordenadas. La notación general y las fórmulas para los símbolos de Christoffel son:

${\ Displaystyle {\ Gamma ^ {i}} _ {ii} = {\ begin {Bmatrix} \, i \, \\ i \, \, i \ end {Bmatrix}} = {\ frac {1} {h_ {i}}} {\ frac {\ parcial h_ {i}} {\ parcial q_ {i}}} \! \; \}$ ${\ Displaystyle {\ Gamma ^ {i}} _ {ij} = \ {\ begin {Bmatrix} \, i \, \\ i \, \, j \ end {Bmatrix}} = {\ frac {1} { h_ {i}}} {\ frac {\ parcial h_ {i}} {\ parcial q_ {j}}} = {\ begin {Bmatrix} \, i \, \\ j \, \, i \ end {Bmatrix }} \! \; \}$ ${\ Displaystyle {\ Gamma ^ {j}} _ {ii} = {\ begin {Bmatrix} \, j \, \\ i \, \, i \ end {Bmatrix}} = - {\ frac {h_ {i }} {{h_ {j}} ^ {2}}} {\ frac {\ parcial h_ {i}} {\ parcial q_ {j}}} \,}$

y el símbolo es cero cuando todos los índices son diferentes. A pesar de las apariencias en contrario, los símbolos de Christoffel no forman los componentes de un tensor . Por ejemplo, son cero en coordenadas cartesianas, pero no en coordenadas polares.

Usando relaciones como esta,

${\ Displaystyle {\ dot {\ boldsymbol {e_ {j}}}} = \ sum _ {k = 1} ^ {d} {\ frac {\ parcial} {\ parcial q_ {k}}} {\ boldsymbol { e_ {j}}} {\ dot {q}} _ {k} \}$

${\ Displaystyle = \ sum _ {k = 1} ^ {d} \ sum _ {i = 1} ^ {d} {\ Gamma ^ {k}} _ {ij} {\ dot {q}} _ {i } {\ boldsymbol {e_ {k}}} \,}$

lo que permite evaluar todas las derivadas de tiempo. Por ejemplo, para la velocidad:

${\ displaystyle {\ boldsymbol {v}} = {\ frac {d} {dt}} {\ boldsymbol {r}} = \ sum _ {k = 1} ^ {d} {\ dot {q}} _ { k} \ {\ boldsymbol {e_ {k}}} + \ sum _ {k = 1} ^ {d} q_ {k} \ {\ dot {\ boldsymbol {e_ {k}}}}}$

${\ Displaystyle = \ sum _ {k = 1} ^ {d} {\ dot {q}} _ {k} \ {\ boldsymbol {e_ {k}}} + \ sum _ {j = 1} ^ {d } q_ {j} \ {\ dot {\ boldsymbol {e_ {j}}}},}$

${\ Displaystyle = \ sum _ {k = 1} ^ {d} {\ dot {q}} _ {k} \ {\ boldsymbol {e_ {k}}} + \ sum _ {k = 1} ^ {d } \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} q_ {j} \ {\ Gamma ^ {k}} _ {ij} {\ boldsymbol {e_ {k} }} {\ dot {q}} _ {i} \}$

${\ Displaystyle = \ sum _ {k = 1} ^ {d} \ left ({\ dot {q}} _ {k} \ + \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} q_ {j} \ {\ Gamma ^ {k}} _ {ij} {\ dot {q}} _ {i} \ right) {\ boldsymbol {e_ {k}}} \,}$

con la notación Γ para los símbolos de Christoffel reemplazando la notación de corchetes. Usando el mismo enfoque, la aceleración es entonces

${\ displaystyle {\ boldsymbol {a}} = {\ frac {d} {dt}} {\ boldsymbol {v}} = \ sum _ {k = 1} ^ {d} {\ dot {v}} _ { k} \ {\ boldsymbol {e_ {k}}} + \ sum _ {k = 1} ^ {d} v_ {k} \ {\ dot {\ boldsymbol {e_ {k}}}} \.}$

${\ Displaystyle = \ sum _ {k = 1} ^ {d} \ left ({\ dot {v}} _ {k} \ + \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} v_ {j} {\ Gamma ^ {k}} _ {ij} {\ dot {q}} _ {i} \ right) {\ boldsymbol {e_ {k}}} \.}$

Al observar la relación de aceleración, la primera suma contiene las derivadas de la velocidad en el tiempo, que se asociarían con la aceleración si fueran coordenadas cartesianas, y la segunda suma (la que tiene los símbolos de Christoffel) contiene términos relacionados con la forma en que cambian los vectores unitarios con tiempo.

Fuerzas ficticias de "estado de movimiento" versus "coordinadas"

Anteriormente en este artículo se introdujo una distinción entre dos terminologías, las fuerzas ficticias que se desvanecen en un marco de referencia inercial se denominan en este artículo fuerzas ficticias de "estado de movimiento" y las que se originan a partir de la diferenciación en un sistema de coordenadas particular son llamadas fuerzas ficticias "coordinadas". Usando la expresión para la aceleración anterior, la ley de movimiento de Newton en el marco de referencia inercial se convierte en:

${\ Displaystyle {\ boldsymbol {F}} = m {\ boldsymbol {a}} = m \ sum _ {k = 1} ^ {d} \ left ({\ dot {v}} _ {k} \ + \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} v_ {j} {\ Gamma ^ {k}} _ {ij} {\ dot {q}} _ {i} \ right) {\ boldsymbol {e_ {k}}} \,}$

donde F es la fuerza real neta sobre la partícula. No hay fuerzas ficticias de "estado de movimiento" porque el marco es inercial, y las fuerzas ficticias del "estado de movimiento" son cero en un marco inercial, por definición.

El enfoque de "coordenadas" de la ley de Newton anterior es retener las derivadas temporales de segundo orden de las coordenadas { q _k } como los únicos términos en el lado derecho de esta ecuación, motivados más por la conveniencia matemática que por la física. Con ese fin, la ley de la fuerza se puede reescribir, tomando la segunda suma del lado de la fuerza de la ecuación como:

${\ Displaystyle {\ boldsymbol {F}} - m \ sum _ {j = 1} ^ {d} \ sum _ {i = 1} ^ {d} v_ {j} {\ Gamma ^ {k}} _ { ij} {\ dot {q}} _ {i} {\ boldsymbol {e_ {k}}} = m {\ tilde {\ boldsymbol {a}}} \,}$

con la convención de que la "aceleración" es ahora: ${\ Displaystyle {\ tilde {\ boldsymbol {a}}}}$

${\ Displaystyle {\ tilde {\ boldsymbol {a}}} = \ sum _ {k = 1} ^ {d} {\ dot {v}} _ {k} {\ boldsymbol {e_ {k}}} \. }$

En la expresión anterior, la suma agregada al lado de la fuerza de la ecuación ahora se trata como si estuvieran presentes "fuerzas" agregadas. Estos términos de suma se denominan habitualmente fuerzas ficticias dentro de este enfoque de "coordenadas", aunque en este marco de referencia inercial todas las fuerzas ficticias del "estado de movimiento" son idénticamente cero. Además, estas "fuerzas" no se transforman en transformaciones de coordenadas como vectores . Así, la designación de los términos de la suma como "fuerzas ficticias" usa esta terminología para contribuciones que son completamente diferentes de cualquier fuerza real y de las fuerzas ficticias del "estado de movimiento". Lo que se suma a esta confusión es que estas fuerzas ficticias "coordinadas" se dividen en dos grupos y reciben los mismos nombres que las fuerzas ficticias de "estado de movimiento", es decir, se dividen en términos "centrífugos" y "Coriolis". , a pesar de su inclusión de términos que no son los términos centrífugos y de Coriolis de "estado de movimiento". Por ejemplo, estos términos centrífugos y de Coriolis de "coordenadas" pueden ser distintos de cero incluso en un marco de referencia inercial donde la fuerza centrífuga del "estado de movimiento" (el tema de este artículo) y la fuerza de Coriolis siempre son cero.

Si el marco no es inercial, por ejemplo, en un marco de referencia giratorio, las fuerzas ficticias del "estado de movimiento" se incluyen en la expresión de fuerza ficticia "coordinada" anterior. Además, si la "aceleración" expresada en términos de derivadas de tiempo de primer orden de la velocidad resulta en términos que no son simplemente derivadas de segundo orden de las coordenadas { q _k } en el tiempo, entonces estos términos que no son de segundo orden. El orden también se lleva al lado de la fuerza de la ecuación y se incluye con las fuerzas ficticias. Desde el punto de vista de una formulación lagrangiana, pueden denominarse fuerzas ficticias generalizadas . Véase Hildebrand, por ejemplo.

La formulación de la dinámica en términos de símbolos de Christoffel y la versión "coordinada" de fuerzas ficticias se utiliza a menudo en el diseño de robots en relación con una formulación lagrangiana de las ecuaciones de movimiento.

notas y referencias

Otras lecturas

• La descripción de Newton en Principia
• Fuerza de reacción centrífuga - Columbia electronic encyclopedia
• M. Alonso y EJ Finn, Física universitaria fundamental , Addison-Wesley
• Fuerza centrípeta frente a fuerza centrífuga : de un tutorial de física en línea del examen Regents del distrito escolar de la ciudad de Oswego
• La fuerza centrífuga actúa hacia adentro cerca de un agujero negro.
• Fuerza centrífuga en el sitio de conceptos de HyperPhysics
• Una lista de enlaces interesantes
• Kenneth Franklin Riley; Michael Paul Hobson; Stephen John Bence (2002). "Derivadas de vectores base y símbolos de Christoffel" . Métodos matemáticos para la física y la ingeniería: una guía completa (2 ed.). Prensa de la Universidad de Cambridge. págs. 814 y sigs . ISBN 0-521-89067-5.

enlaces externos

• Movimiento sobre una superficie plana de Java Physlet por Brian Fiedler (de la Escuela de Meteorología de la Universidad de Oklahoma) que ilustra fuerzas ficticias. El fislet muestra tanto la perspectiva vista desde un punto de vista giratorio como no giratorio.
• Movimiento sobre una superficie parabólica de Java physlet por Brian Fiedler (de la Escuela de Meteorología de la Universidad de Oklahoma) que ilustra fuerzas ficticias. El fislet muestra tanto la perspectiva vista desde un punto de vista giratorio como desde un punto de vista no giratorio.
• Clip de animación que muestra escenas vistas desde un marco inercial y un marco de referencia giratorio, visualizando el Coriolis y las fuerzas centrífugas.
• Fuerzas centrípetas y centrífugas en MathPages
• Fuerza centrífuga en h2g2
• John Baez: ¿La fuerza centrífuga sostiene a la Luna?

Ver también