Funciones hiperbolasticas - Hyperbolastic functions

Gráfico que describe la función Hiperbolastica Tipo I con valores de parámetros variables.

Gráfico que describe la función Hiperbolastica Tipo I con valores de parámetros variables.

Gráfico que describe la función Hiperbolastica Tipo II con valores de parámetros variables.

Gráfico que describe la función Hiperbolastica Tipo II con valores de parámetros variables.

Gráfico que describe la función Hiperbolastica Tipo III con valores de parámetros variables.

Gráfico que describe la función de distribución acumulativa hiperbolastica de tipo III con valores variables de los parámetros.

Gráfico que describe la función de densidad de probabilidad hiperbolastica de tipo III con valores de parámetros variables.

Las funciones hipérbolasticas , también conocidas como modelos de crecimiento hipérbolásticas , son funciones matemáticas que se utilizan en el modelado estadístico médico . Estos modelos se desarrollaron originalmente para capturar la dinámica de crecimiento de las esferas de tumores multicelulares y fueron introducidos en 2005 por Mohammad Tabatabai, David Williams y Zoran Bursac. La precisión de las funciones hipérbolasticas en el modelado de problemas del mundo real se debe en parte a su flexibilidad en su punto de inflexión. Estas funciones pueden usarse en una amplia variedad de problemas de modelado tales como crecimiento tumoral, proliferación de células madre , cinética farmacéutica, crecimiento del cáncer, función de activación sigmoidea en redes neuronales y progresión o regresión de enfermedades epidemiológicas.

Las funciones hipérbolasticas pueden modelar tanto las curvas de crecimiento como las de desintegración hasta que alcanza la capacidad de carga . Debido a su flexibilidad, estos modelos tienen diversas aplicaciones en el campo médico, con la capacidad de capturar la progresión de la enfermedad con un tratamiento intermedio. Como indican las figuras, las funciones hipérbolasticas pueden ajustarse a una curva sigmoidea que indica que la tasa más lenta ocurre en las etapas temprana y tardía. Además de presentar formas sigmoideas, también puede adaptarse a situaciones bifásicas en las que las intervenciones médicas ralentizan o revierten la progresión de la enfermedad; pero, cuando el efecto del tratamiento se desvanece, la enfermedad iniciará la segunda fase de su progresión hasta alcanzar su asíntota horizontal.

Una de las principales características que tienen estas funciones es que no solo pueden ajustarse a formas sigmoideas, sino que también pueden modelar patrones de crecimiento bifásico que otras curvas sigmoideas clásicas no pueden modelar adecuadamente. Esta característica distintiva tiene aplicaciones ventajosas en varios campos que incluyen medicina, biología, economía, ingeniería, agronomía y teoría de sistemas asistidos por computadora.

Función H1

La ecuación de velocidad hipérbolastica de tipo I , denominada H1, viene dada por:

$${\ Displaystyle {\ frac {dP (x)} {dx}} = {\ frac {P (x)} {M}} \ left (MP \ left (x \ right) \ right) \ left (\ delta + {\ frac {\ theta} {\ sqrt {1 + x ^ {2}}}} \ right),}$$

donde es cualquier número real y es el tamaño de la población en . El parámetro representa la capacidad de carga y los parámetros y conjuntamente representan la tasa de crecimiento. El parámetro da la distancia desde una curva sigmoidea simétrica. Resolver la ecuación de tasa hipérbolastica de tipo I para da: ${\ Displaystyle x}$${\ Displaystyle P \ left (x \ right)}$${\ Displaystyle x}$${\ Displaystyle M}$${\ Displaystyle \ delta}$${\ Displaystyle \ theta}$${\ Displaystyle \ theta}$${\ Displaystyle P \ left (x \ right)}$

$${\ Displaystyle P (x) = {\ frac {M} {1+ \ alpha e ^ {- \ delta x- \ theta \ operatorname {arsinh} (x)}}},}$$

donde es la función del seno hiperbólico inverso . Si uno desea usar la condición inicial , entonces se puede expresar como: ${\ Displaystyle \ operatorname {arsinh}}$${\ Displaystyle P \ left (x_ {0} \ right) = P_ {0}}$${\ Displaystyle \ alpha}$

${\ Displaystyle \ alpha = {\ frac {M-P_ {0}} {P_ {0}}} e ^ {\ delta x_ {0} + \ theta \ operatorname {arsinh} (x_ {0})}}$.

Si , entonces se reduce a: ${\ Displaystyle x_ {0} = 0}$${\ Displaystyle \ alpha}$

${\ Displaystyle \ alpha = {\ frac {M-P_ {0}} {P_ {0}}}}$.

La función hipérbolastica de tipo I generaliza la función logística . Si los parámetros , entonces se convertiría en una función logística. Esta función es una función de tipo I hyperbolastic . La función hipérbolastica estándar del tipo I es ${\ Displaystyle \ theta = 0}$${\ Displaystyle P (x)}$

${\ Displaystyle P (x) = {\ frac {1} {1 + e ^ {- x- \ operatorname {arsinh} (x)}}}}$.

Función H2

La ecuación de tasa hipérbolastica de tipo II , denotada por H2, se define como:

${\ Displaystyle {\ frac {dP (x)} {dx}} = {\ frac {\ alpha \ delta \ gamma P ^ {2} (x) x ^ {\ gamma -1}} {M}} \ tanh \ left ({\ frac {MP (x)} {\ alpha P (x)}} \ right),}$

donde es la tangente hiperbólica función, es la capacidad de carga, y ambos y determinar conjuntamente la tasa de crecimiento. Además, el parámetro representa la aceleración en el transcurso del tiempo. Resolviendo la función de tasa hipérbolastica de tipo II para da: ${\ Displaystyle \ tanh}$${\ Displaystyle M}$${\ Displaystyle \ delta}$${\ Displaystyle \ gamma> 0}$${\ Displaystyle \ gamma}$${\ Displaystyle P \ left (x \ right)}$

${\ Displaystyle P (x) = {\ frac {M} {1+ \ alpha \ operatorname {arsinh} \ left (e ^ {- \ delta x ^ {\ gamma}} \ right)}}}$.

Si se desea utilizar la condición inicial, se puede expresar como: ${\ Displaystyle P (x_ {0}) = P_ {0},}$${\ Displaystyle \ alpha}$

${\ displaystyle \ alpha = {\ frac {M-P_ {0}} {P_ {0} \ operatorname {arsinh} \ left (e ^ {- \ delta x_ {0} ^ {\ gamma}} \ right)} }}$.

Si , entonces se reduce a: ${\ Displaystyle x_ {0} = 0}$${\ Displaystyle \ alpha}$

${\ Displaystyle \ alpha = {\ frac {M-P_ {0}} {P_ {0} \ operatorname {arsinh} (1)}}}$.

La función hipérbolastica estándar del tipo II se define como:

${\ Displaystyle P (x) = {\ frac {1} {1+ \ operatorname {arsinh} \ left (e ^ {- x} \ right)}}}$.

Función H3

La ecuación de tasa hipérbolastica de tipo III se denota por H3 y tiene la forma:

${\ Displaystyle {\ frac {dP (t)} {dt}} = \ left (MP \ left (t \ right) \ right) \ left (\ delta \ gamma t ^ {\ gamma -1} + {\ frac {\ theta} {\ sqrt {1+ \ theta ^ {2} t ^ {2}}}} \ right)}$,

donde > 0. El parámetro representa la capacidad de carga, y los parámetros y determinar conjuntamente la tasa de crecimiento. El parámetro representa la aceleración de la escala de tiempo, mientras que el tamaño de representa la distancia desde una curva sigmoidea simétrica. La solución a la ecuación diferencial de tipo III es: ${\ Displaystyle t}$${\ Displaystyle M}$${\ Displaystyle \ delta,}$ ${\ Displaystyle \ gamma,}$${\ Displaystyle \ theta}$${\ Displaystyle \ gamma,}$${\ Displaystyle \ theta}$

${\ Displaystyle P (t) = M- \ alpha e ^ {- \ delta t ^ {\ gamma} - \ operatorname {arsinh} (\ theta t)}}$,

con la condición inicial podemos expresar como: ${\ Displaystyle P \ left (t_ {0} \ right) = P_ {0}}$${\ Displaystyle \ alpha}$

${\ Displaystyle \ alpha = \ left (M-P_ {0} \ right) e ^ {\ delta t_ {0} ^ {\ gamma} + \ operatorname {arsinh} (\ theta t_ {0})}}$.

La distribución hipérbolastica de tipo III es una familia de tres parámetros de distribuciones de probabilidad continuas con parámetros de escala > 0 y ≥ 0 y parámetro como parámetro de forma . Cuando el parámetro = 0, la distribución hipérbolastica del tipo III se reduce a la distribución de Weibull . La función de distribución acumulativa hipérbolastica del tipo III viene dada por: ${\ Displaystyle \ delta}$${\ Displaystyle \ theta}$${\ Displaystyle \ gamma}$${\ Displaystyle \ theta}$

${\ displaystyle F (x; \ delta, \ gamma, \ theta) = {\ begin {cases} 1-e ^ {- \ delta x ^ {\ gamma} - \ operatorname {arsinh} (\ theta x)} & x \ geq 0, \\ 0 & x <0 \ end {cases}}}$,

y su función de densidad de probabilidad correspondiente es:

${\ displaystyle f (x; \ delta, \ gamma, \ theta) = {\ begin {cases} e ^ {- \ delta x ^ {\ gamma} - \ operatorname {arsinh} (\ theta x)} \ left ( \ delta \ gamma x ^ {\ gamma -1} + {\ frac {\ theta} {\ sqrt {1+ \ theta ^ {2} x ^ {2}}}} \ right) & x \ geq 0, \\ 0 & x <0 \ end {cases}}}$.

La función de peligro (o tasa de falla) viene dada por: ${\ Displaystyle h}$

${\ Displaystyle h \ left (x; \ delta, \ gamma, \ theta \ right) = \ delta \ gamma x ^ {\ gamma -1} + {\ frac {\ theta} {\ sqrt {1 + x ^ { 2} \ theta ^ {2}}}}.}$

La función de supervivencia viene dada por: ${\ Displaystyle S}$

${\ Displaystyle S (x; \ delta, \ gamma, \ theta) = e ^ {- \ delta x ^ {\ gamma} - \ operatorname {arsinh} (\ theta x)}.}$

La función de distribución acumulativa hiperbolastica estándar del tipo III se define como:

${\ Displaystyle F \ left (x \ right) = 1-e ^ {- x- \ operatorname {arsinh} (x)}}$,

y su función de densidad de probabilidad correspondiente es:

${\ Displaystyle f (x) = e ^ {- x- \ operatorname {arsinh} (x)} \ left (1 + {\ frac {1} {\ sqrt {1 + x ^ {2}}}} \ right )}$.

Propiedades

Si se desea calcular el punto donde la población alcanza un porcentaje de su capacidad de carga , entonces se puede resolver la ecuación: ${\ Displaystyle x}$${\ Displaystyle M}$

${\ Displaystyle P (x) = kM}$

para , donde . Por ejemplo, el medio punto se puede encontrar configurando . ${\ Displaystyle x}$${\ Displaystyle 0 <k <1}$${\ Displaystyle k = {\ frac {1} {2}}}$

Aplicaciones

Gráfico hiperbolastico 3D de la biomasa de fitoplancton en función de la concentración de nutrientes y el tiempo

Según los investigadores de células madre del Instituto McGowan de Medicina Regenerativa de la Universidad de Pittsburgh, "un modelo más nuevo [llamado hipérbolastic tipo III o] H3 es una ecuación diferencial que también describe el crecimiento celular. Este modelo permite mucha más variación y tiene se ha demostrado que predice mejor el crecimiento ".

Los modelos de crecimiento hiperbólico H1, H2 y H3 se han aplicado para analizar el crecimiento del carcinoma de Ehrlich sólido utilizando una variedad de tratamientos.

En ciencia animal, las funciones hipérbolasticas se han utilizado para modelar el crecimiento de pollos de engorde. Se utilizó el modelo hipérbolastico de tipo III para determinar el tamaño de la herida en recuperación.

En el área de la cicatrización de heridas, los modelos hipérbolasticos representan con precisión el curso temporal de la cicatrización. Estas funciones se han utilizado para investigar variaciones en la velocidad de curación entre diferentes tipos de heridas y en diferentes etapas del proceso de curación, teniendo en cuenta las áreas de oligoelementos, factores de crecimiento, heridas diabéticas y nutrición.

Otra aplicación de las funciones hipérbolasticas se encuentra en el área del proceso de difusión estocástica , cuya función media es una curva hipérbolastica. Se estudian las principales características del proceso y se considera la estimación de máxima verosimilitud para los parámetros del proceso. Con este fin, el algoritmo de optimización metaheurística de luciérnaga se aplica después de delimitar el espacio paramétrico mediante un procedimiento por etapas. Algunos ejemplos basados ​​en rutas de muestra simuladas y datos reales ilustran este desarrollo. Una ruta de muestra de un proceso de difusión modela la trayectoria de una partícula incrustada en un fluido que fluye y sometida a desplazamientos aleatorios debido a colisiones con otras partículas, lo que se denomina movimiento browniano . La función hipérbolastica del tipo III se utilizó para modelar la proliferación de células madre embrionarias y mesenquimales adultas ; y el modelo mixto hipérbolastico de tipo II se ha utilizado para modelar los datos del cáncer de cuello uterino . Las curvas hiperbolasticas pueden ser una herramienta importante en el análisis del crecimiento celular, el ajuste de curvas biológicas y el crecimiento del fitoplancton .

En ecología y manejo forestal , los modelos hipérbolasticos se han aplicado para modelar la relación entre DAP y altura.

El modelo hipérbolastico multivariable tipo III se ha utilizado para analizar la dinámica de crecimiento del fitoplancton teniendo en cuenta la concentración de nutrientes.

Regresiones hiperbolasticas

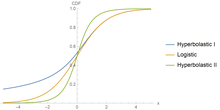
Función de distribución acumulativa de tipo hiperbolastico I, logístico e hiperbolastico tipo II

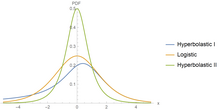
PDF de H1, Logística y H2

Las regresiones hipérbolasticas son modelos estadísticos que utilizan funciones hipérbolasticas estándar para modelar una variable de resultado dicotómica o multinomial . El propósito de la regresión hipérbolastica es predecir un resultado usando un conjunto de variables explicativas (independientes). Estos tipos de regresiones se utilizan de forma rutinaria en muchas áreas, incluidas las ciencias médicas, de salud pública, dentales, biomédicas, así como sociales, del comportamiento y de la ingeniería. Por ejemplo, el análisis de regresión binaria se ha utilizado para predecir lesiones endoscópicas en la anemia por deficiencia de hierro . Además, se aplicó regresión binaria para diferenciar entre masa anexial maligna y benigna antes de la cirugía.

La regresión hipérbolastica binaria de tipo I

Sea una variable de resultado binaria que puede asumir uno de dos valores mutuamente excluyentes, éxito o fracaso. Si codificamos el éxito como y el fracaso como , entonces la probabilidad de éxito hipérbolastica del tipo I con una muestra de tamaño en función del vector de parámetros dado un vector dimensional de variables explicativas se define como , donde , viene dada por: ${\ Displaystyle Y}$${\ Displaystyle Y = 1}$${\ Displaystyle Y = 0}$${\ Displaystyle n}$${\ displaystyle {\ boldsymbol {\ beta}} = (\ beta _ {0}, \ beta _ {1}, \ ldots, \ beta _ {p})}$${\ Displaystyle p}$${\ Displaystyle \ mathbf {x} _ {i} = (x_ {i1}, \ x_ {i2}, \ ldots, \ x_ {ip}) ^ {T}}$${\ Displaystyle i = 1,2, \ ldots, n}$

${\ Displaystyle \ pi (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = P (y_ {i} = 1 | \ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = {\ frac {1} {1 + e ^ {- (\ beta _ {0} + \ sum _ {s = 1} ^ {p} {\ beta _ {s} x_ {is}} ) - \ operatorname {arsinh} (\ beta _ {0} + \ sum _ {s = 1} ^ {p} {\ beta _ {s} x_ {is}})}}}}$.

Las probabilidades de éxito son la relación entre la probabilidad de éxito y la probabilidad de fracaso. Para la regresión hipérbolastica binaria de tipo I, las probabilidades de éxito se denotan y se expresan mediante la ecuación: ${\ Displaystyle Odds_ {H1}}$

${\ Displaystyle Odds_ {H1} = e ^ {\ beta _ {0} + \ sum _ {s = 1} ^ {p} {\ beta _ {s} x_ {is}} + \ operatorname {arsinh} (\ beta _ {0} + \ sum _ {s = 1} ^ {p} {\ beta _ {s} x_ {is}})}}$.

El logaritmo de se llama logit de regresión hipérbolastica binaria de tipo I. La transformación logit se denota y se puede escribir como: ${\ Displaystyle Odds_ {H1}}$${\ Displaystyle L_ {H1}}$

${\ Displaystyle L_ {H1} = \ beta _ {0} + \ sum _ {s = 1} ^ {p} {\ beta _ {s} x_ {is}} + \ operatorname {arsinh} [\ beta _ { 0} + \ sum _ {s = 1} ^ {p} {\ beta _ {s} x_ {is}}]}$.

La regresión hipérbolastica binaria del tipo II

La regresión hipérbolastica de tipo II es un método alternativo para el análisis de datos binarios con propiedades robustas. Para la variable de resultado binaria , la probabilidad de éxito hipérbolastica del tipo II es una función de un vector dimensional de la variable explicativa es: ${\ Displaystyle Y}$${\ Displaystyle p}$${\ Displaystyle \ mathbf {x} _ {i}}$

${\ Displaystyle \ pi (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = P (y_ {i} = 1 | \ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = {\ frac {1} {1+ \ operatorname {arsinh} [e ^ {- (\ beta _ {0} + \ sum _ {s = 1} ^ {p} {\ beta _ {s " } x_ {es}})}]}}}$ ,

Para la regresión hipérbolastica binaria de tipo II, las probabilidades de éxito se denotan y se definen como: ${\ Displaystyle Odds_ {H2}}$

${\ Displaystyle Odds_ {H2} = {\ frac {1} {\ operatorname {arsinh} [e ^ {- (\ beta _ {0} + \ sum _ {s = 1} ^ {p} {\ beta _ { s} x_ {is}})}]}}.}$

La transformación logit viene dada por: ${\ Displaystyle L_ {H2}}$

${\ Displaystyle L_ {H2} = - \ log {(\ operatorname {arsinh} [e ^ {- (\ beta _ {0} + \ sum _ {s = 1} ^ {p} {\ beta _ {s} ") x_ {is}})}])}}$

Estimación de parámetros para la regresión hipérbolastica binaria de tipo I y II

La estimación del vector de parámetros se puede obtener maximizando la función de verosimilitud logarítmica: ${\ displaystyle {\ boldsymbol {\ beta}}}$

${\ displaystyle {\ hat {\ beta}} = {\ underset {\ boldsymbol {\ beta}} {\ operatorname {argmax}}} {\ sum _ {i = 1} ^ {n} [y_ {i} ln (\ pi (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})) + (1-y_ {i}) ln (1- \ pi (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}))]}}$

donde se define de acuerdo con uno de los dos tipos de funciones hiberbolásticas utilizadas. ${\ Displaystyle \ pi (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})}$

La regresión hipérbolastica multinomial de tipo I y II

La generalización de la regresión hipérbolastica binaria a la regresión hipérbolastica multinomial tiene una variable de respuesta para el individuo con categorías (es decir ). Cuando , este modelo se reduce a una regresión hipérbolastica binaria. Para cada uno , formamos variables indicadoras donde ${\ Displaystyle y_ {i}}$${\ Displaystyle i}$${\ Displaystyle k}$${\ Displaystyle y_ {i} \ in \ {1,2, \ ldots, k \}}$${\ Displaystyle k = 2}$${\ Displaystyle i = 1,2, \ ldots, n}$${\ Displaystyle k-1}$${\ Displaystyle y_ {ij}}$

${\ displaystyle y_ {ij} = {\ begin {cases} 1 & {\ text {if}} y_ {i} = j, \\ 0 & {\ text {if}} y_ {i} \ neq j \ end {cases }}}$,

lo que significa que siempre que la respuesta sea de categoría y de otro tipo. ${\ Displaystyle y_ {ij} = 1}$${\ Displaystyle i ^ {th}}$${\ Displaystyle j}$${\ Displaystyle 0}$

Defina el vector de parámetros con , un vector cero en un espacio euclidiano -dimensional y . ${\ Displaystyle {\ boldsymbol {\ beta}} _ {j} = (\ beta _ {j0}, \ beta _ {j1}, \ ldots, \ beta _ {jp})}$${\ Displaystyle \ beta _ {0}}$${\ Displaystyle p + 1}$${\ displaystyle {\ boldsymbol {\ beta}} = ({\ boldsymbol {\ beta}} _ {1}, \ ldots, {\ boldsymbol {\ beta}} _ {k-1}) ^ {T}}$

Utilizando la categoría 1 como referencia y como su función de probabilidad correspondiente, la regresión hipérbolastica multinomial de probabilidades de tipo I se define como: ${\ Displaystyle \ pi _ {1} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})}$

${\ Displaystyle \ pi _ {1} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = P (y_ {i} = 1 | \ mathbf {x} _ {i}; { \ boldsymbol {\ beta}}) = {\ frac {1} {1+ \ sum _ {s = 1} ^ {k-1} e ^ {- \ eta _ {s} (\ mathbf {x} _ { i}; {\ boldsymbol {\ beta}}) - arsinh [\ eta _ {s} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})]}}}}$

y para , ${\ Displaystyle j = 2, \ ldots, k-1}$

${\ Displaystyle \ pi _ {j} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = P (y_ {i} = j | \ mathbf {x} _ {i}; { \ boldsymbol {\ beta}}) = {\ frac {e ^ {- \ eta _ {j} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) - arsinh [\ eta _ { j} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})]}} {1+ \ sum _ {s = 1} ^ {k-1} e ^ {- \ eta _ { s} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) - arsinh [\ eta _ {s} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}} )]}}}}$

De manera similar, para la regresión hipérbolastica multinomial de tipo II tenemos:

${\ Displaystyle \ pi _ {1} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = P (y_ {i} = 1 | \ mathbf {x} _ {i}; { \ boldsymbol {\ beta}}) = {\ frac {1} {1+ \ sum _ {s = 1} ^ {k-1} arsinh [e ^ {- \ eta _ {s} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})}]}}}$

y para , ${\ Displaystyle j = 2, \ ldots, k-1}$

${\ Displaystyle \ pi _ {j} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = P (y_ {i} = j | \ mathbf {x} _ {i}; { \ boldsymbol {\ beta}}) = {\ frac {arsinh [e ^ {- \ eta _ {j} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})}]} {1 + \ sum _ {s = 1} ^ {k-1} arsinh [e ^ {- \ eta _ {s} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})}]} }}$

Para cada uno en la regresión hipérbolastica multinomial de tipo I y II, ${\ Displaystyle i}$

${\ Displaystyle \ pi _ {k} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = 1- \ sum _ {j = 1} ^ {k-1} \ pi _ { j} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})}$

El log-odds de pertenencia a la categoría frente a la categoría de referencia 1, denotado por , es igual a ${\ Displaystyle j}$${\ Displaystyle \ eta _ {j} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})}$

${\ Displaystyle \ eta _ {j} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}}) = ln [{\ frac {\ pi _ {j} (\ mathbf {x} _ { i}; {\ boldsymbol {\ beta}})} {\ pi _ {1} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})}}] = \ beta _ {j0} + \ beta _ {j1} x_ {i1} + \ ldots + \ beta _ {jp} x_ {ip}}$

donde y . La matriz de parámetros estimada de la regresión hipérbolastica multinomial se obtiene maximizando la función logarítmica de verosimilitud. Las estimaciones de máxima verosimilitud de la matriz de parámetros es ${\ Displaystyle j = 1, \ ldots, k-1}$${\ Displaystyle i = 1, \ ldots, n}$${\ Displaystyle {\ hat {\ boldsymbol {\ beta}}}}$${\ displaystyle {\ boldsymbol {\ beta}}}$

${\ displaystyle {\ boldsymbol {\ hat {\ beta}}} = {\ underset {\ boldsymbol {\ beta}} {\ operatorname {argmax}}} {\ sum _ {i = 1} ^ {n} (y_ {i1} ln [\ pi _ {1} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta}})] + y_ {i2} ln [\ pi _ {2} (\ mathbf {x } _ {i}; {\ boldsymbol {\ beta}})] + \ ldots + y_ {ik} ln [\ pi _ {k} (\ mathbf {x} _ {i}; {\ boldsymbol {\ beta} })])}}$

Referencias