La "integración gaussiana" vuelve a dirigir aquí. Para la integral de una función gaussiana, vea
integral gaussiana .
En el análisis numérico , una regla de cuadratura es una aproximación de la integral definida de una función , generalmente expresada como una suma ponderada de valores de función en puntos específicos dentro del dominio de integración. (Ver integración numérica para más información sobre las reglas de cuadratura ). Una regla de cuadratura gaussiana de n puntos , llamada así por Carl Friedrich Gauss , es una regla de cuadratura construida para producir un resultado exacto para polinomios de grado 2 n - 1 o menos mediante una elección adecuada de los nodos x i y pesos w i para i = 1, ..., n . La formulación moderna que utiliza polinomios ortogonales fue desarrollada por Carl Gustav Jacobi en 1826. El dominio de integración más común para tal regla se toma como [−1, 1] , por lo que la regla se establece como

que es exacta para polinomios de grado 2 n - 1 o menos. Esta regla exacta se conoce como regla de cuadratura de Gauss-Legendre. La regla de la cuadratura solo será una aproximación precisa a la integral anterior si f ( x ) está bien aproximada por un polinomio de grado 2 n - 1 o menos en [−1, 1] .
La regla de cuadratura de Gauss- Legendre no se usa típicamente para funciones integrables con singularidades de punto final . En cambio, si el integrando se puede escribir como

donde g ( x ) está bien aproximado por un polinomio de bajo grado, entonces los nodos y pesos alternativos normalmente darán reglas de cuadratura más precisas. Estas se conocen como reglas de cuadratura de Gauss-Jacobi , es decir,



Los pesos comunes incluyen ( Chebyshev-Gauss ) y . También se puede querer integrar sobre intervalos semi-infinitos ( cuadratura de Gauss-Laguerre ) e infinitos ( cuadratura de Gauss-Hermite ).


Se puede demostrar (ver Press, et al., O Stoer y Bulirsch) que los nodos en cuadratura x i son las raíces de un polinomio que pertenece a una clase de polinomios ortogonales (la clase ortogonal con respecto a un producto interno ponderado). Ésta es una observación clave para calcular los nodos y pesos en cuadratura de Gauss.
Cuadratura de Gauss-Legendre
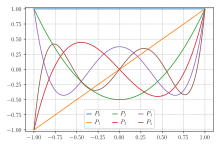
Gráficas de polinomios de Legendre (hasta
n = 5)
Para el problema de integración más simple mencionado anteriormente, es decir, f ( x ) está bien aproximado por polinomios en , los polinomios ortogonales asociados son polinomios de Legendre , denotados por P n ( x ) . Con el n -ésimo polinomio normalizado para dar P n (1) = 1 , el i -ésimo nodo de Gauss, x i , es la i -ésima raíz de P n y los pesos están dados por la fórmula ( Abramowitz y Stegun 1972 , pág.887)![[-1, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) error de harv: sin destino: CITEREFAbramowitzStegun1972 ( ayuda )
error de harv: sin destino: CITEREFAbramowitzStegun1972 ( ayuda )
![{\ Displaystyle w_ {i} = {\ frac {2} {\ left (1-x_ {i} ^ {2} \ right) \ left [P '_ {n} (x_ {i}) \ right] ^ {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a5533b3b5d42f1c60c3c5e6e5d62c37c2878a3)
Algunas reglas de cuadratura de orden inferior se tabulan a continuación (en el intervalo [−1, 1] , consulte la sección siguiente para conocer otros intervalos).
| Número de puntos, n
|
Puntos, x i
|
Pesos, w i
|
| 1
|
0
|
2
|
| 2
|
 |
± 0,57735 ...
|
1
|
| 3
|
0
|
 |
0,888889 ...
|
 |
± 0,774597 ...
|
 |
0,555556 ...
|
| 4
|
 |
± 0,339981 ...
|
 |
0,652145 ...
|
 |
± 0,861136 ...
|
 |
0,347855 ...
|
| 5
|
0
|
 |
0,568889 ...
|
 |
± 0,538469 ...
|
 |
0,478629 ...
|
 |
± 0,90618 ...
|
 |
0,236927 ...
|
Cambio de intervalo
Una integral sobre [ a , b ] debe cambiarse a una integral sobre [−1, 1] antes de aplicar la regla de cuadratura gaussiana. Este cambio de intervalo se puede realizar de la siguiente manera:

con 
La aplicación de la regla de cuadratura de Gauss de puntos da como resultado la siguiente aproximación:



Ejemplo de regla de cuadratura de Gauss de dos puntos
Use la regla de cuadratura de Gauss de dos puntos para aproximar la distancia en metros cubierta por un cohete de a como lo indica



Cambie los límites para poder usar los pesos y las abscisas que se dan en la Tabla 1. Además, encuentre el error verdadero relativo absoluto. El valor real se da como 11061,34 m
Solución
Primero, cambie los límites de integración de a da



A continuación, obtenga los factores de ponderación y los valores de los argumentos de la función de la Tabla 1 para la regla de dos puntos,




Ahora podemos usar la fórmula de cuadratura de Gauss

ya que


Dado que el valor verdadero es 11061.34m, el error verdadero relativo absoluto es


Otras formas
El problema de integración se puede expresar de una manera un poco más general introduciendo una función de ponderación positiva ω en el integrando y permitiendo un intervalo distinto de [−1, 1] . Es decir, el problema es calcular

para algunas opciones de una , b , y ω . Para a = −1 , b = 1 y ω ( x ) = 1 , el problema es el mismo que se consideró anteriormente. Otras opciones conducen a otras reglas de integración. Algunos de estos se tabulan a continuación. Los números de ecuación se dan para Abramowitz y Stegun (A & S).
| Intervalo
|
ω ( x )
|
Polinomios ortogonales
|
COMO
|
Para más información, ver ...
|
| [−1, 1] |
1 |
Polinomios de Legendre |
25.4.29 |
§ Cuadratura de Gauss-Legendre
|
| (−1, 1) |
 |
Polinomios de Jacobi |
25.4.33 ( β = 0 ) |
Cuadratura de Gauss-Jacobi
|
| (−1, 1) |
 |
Polinomios de Chebyshev (primer tipo) |
25.4.38 |
Cuadratura de Chebyshev-Gauss
|
| [−1, 1] |
 |
Polinomios de Chebyshev (segundo tipo) |
25.4.40 |
Cuadratura de Chebyshev-Gauss
|
| [0, ∞) |
 |
Polinomios de Laguerre |
25.4.45 |
Cuadratura de Gauss-Laguerre
|
| [0, ∞) |
 |
Polinomios de Laguerre generalizados
|
|
Cuadratura de Gauss-Laguerre
|
| (−∞, ∞) |
 |
Polinomios de Hermite |
25.4.46 |
Cuadratura de Gauss-Hermite
|
Teorema fundamental
Sea p n un polinomio no trivial de grado n tal que

Si elegimos los n nodos x i para que sean los ceros de p n , entonces existen n pesos w i que hacen que la integral calculada en cuadratura de Gauss sea exacta para todos los polinomios h ( x ) de grado 2 n - 1 o menos. Además, todos estos nodos x i estarán en el intervalo abierto ( a , b ) ( Stoer y Bulirsch 2002 , pp. 172-175).
Se dice que el polinomio p n es un polinomio ortogonal de grado n asociado a la función de ponderación ω ( x ) . Es único hasta un factor de normalización constante. La idea subyacente a la prueba es que, debido a su grado suficientemente bajo, h ( x ) se puede dividir por para producir un cociente q ( x ) de grado estrictamente menor que n , y un resto r ( x ) de grado aún menor, de modo que ambos serán ortogonales a , por la propiedad definitoria de . Por lo tanto




Debido a la elección de los nodos x i , la relación correspondiente

sostiene también. La exactitud de la integral calculada para entonces se sigue de exactitud correspondiente para polinomios de grado solamente n o menos (como es ).


Fórmula general para los pesos
Los pesos se pueden expresar como
-
 |
|
( 1 )
|
donde es el coeficiente de en . Para probar esto, tenga en cuenta que utilizando la interpolación de Lagrange se puede expresar r ( x ) en términos de como





porque r ( x ) tiene un grado menor que n y, por lo tanto, está fijado por los valores que alcanza en n puntos diferentes. Multiplicando ambos lados por ω ( x ) e integrando de a a b da como resultado

Por tanto, los pesos w i vienen dados por

Esta expresión integral para se puede expresar en términos de polinomios ortogonales y de la siguiente manera.



Podemos escribir

donde es el coeficiente de en . Tomando el límite de x a los rendimientos usando la regla de L'Hôpital





Por tanto, podemos escribir la expresión integral para los pesos como
-
 |
|
( 2 )
|
En el integrando, escribiendo

rendimientos

siempre , porque


es un polinomio de grado k - 1 que es ortogonal a . Entonces, si q ( x ) es un polinomio de como máximo n-ésimo grado, tenemos


Podemos evaluar la integral del lado derecho de la siguiente manera. Como es un polinomio de grado n - 1 , tenemos



donde s ( x ) es un polinomio de grado . Como s ( x ) es ortogonal a tenemos



Entonces podemos escribir

El término entre paréntesis es un polinomio de grado , que por lo tanto es ortogonal a . Por tanto, la integral se puede escribir como



De acuerdo con la ecuación ( 2 ), los pesos se obtienen dividiendo esto por y eso da como resultado la expresión en la ecuación ( 1 ).

 también se puede expresar en términos de polinomios ortogonales y ahora . En la relación de recurrencia de 3 términos, el término con desaparece, por lo que en la Ec. (1) se puede reemplazar por .
también se puede expresar en términos de polinomios ortogonales y ahora . En la relación de recurrencia de 3 términos, el término con desaparece, por lo que en la Ec. (1) se puede reemplazar por .






Prueba de que los pesos son positivos
Considere el siguiente polinomio de grado 

donde, como arriba, x j son las raíces del polinomio . Claramente . Dado que el grado de es menor que , se aplica la fórmula de cuadratura gaussiana que involucra los pesos y nodos obtenidos de . Dado que para j no es igual a i, tenemos







Dado que ambos y son funciones no negativas, se deduce que .



Cálculo de las reglas de cuadratura de Gauss
Existen muchos algoritmos para calcular los nodos x i y los pesos w i de las reglas de cuadratura de Gauss. Los más populares son el algoritmo de Golub-Welsch que requiere operaciones O ( n 2 ) , el método de Newton para resolver utilizando la recurrencia de tres términos para la evaluación que requiere operaciones O ( n 2 ) y las fórmulas asintóticas para n grandes que requieren operaciones O ( n ) .

Relación de recurrencia
Los polinomios ortogonales con for para un producto escalar , grado y coeficiente principal uno (es decir, polinomios ortogonales monicos ) satisfacen la relación de recurrencia






y producto escalar definido

porque donde n es el grado máximo que puede tomarse como infinito, y donde . En primer lugar, los polinomios definidos por la relación de recurrencia que comienza con tienen un coeficiente principal uno y un grado correcto. Dado el punto de partida por , la ortogonalidad de puede mostrarse por inducción. Porque uno tiene







Ahora bien, si son ortogonales, entonces también , porque en



todos los productos escalares se desvanecen excepto el primero y el que se encuentra con el mismo polinomio ortogonal. Por lo tanto,


Sin embargo, si el producto escalar satisface (que es el caso de la cuadratura gaussiana), la relación de recurrencia se reduce a una relación de recurrencia de tres términos: For es un polinomio de grado menor o igual a r - 1 . Por otro lado, es ortogonal a todo polinomio de grado menor o igual a r - 1 . Por lo tanto, se tiene y para s < r - 1 . La relación de recurrencia luego se simplifica a






o

(con la convención ) donde


(el último debido a , ya que difiere de en un grado menor que r ).



El algoritmo de Golub-Welsch
La relación de recurrencia de tres términos se puede escribir en forma de matriz donde , es el vector base estándar, es decir ,, y J es la llamada matriz de Jacobi:






Los ceros de los polinomios hasta el grado n , que se utilizan como nodos para la cuadratura gaussiana, se pueden encontrar calculando los valores propios de esta matriz tridiagonal . Este procedimiento se conoce como algoritmo de Golub-Welsch .

Para calcular los pesos y los nodos, es preferible considerar la matriz tridiagonal simétrica con elementos


J yson matrices similares y, por lo tanto, tienen los mismos valores propios (los nodos). Los pesos se pueden calcular a partir de los autovectores correspondientes: Sies un autovector normalizado (es decir, un autovector con norma euclidiana igual a uno) asociado al autovalor x j , el peso correspondiente se puede calcular a partir del primer componente de este autovector, a saber:



donde es la integral de la función de peso


Ver, por ejemplo, ( Gil, Segura & Temme 2007 ) para más detalles.
Estimaciones de error
El error de una regla de cuadratura gaussiana se puede establecer de la siguiente manera ( Stoer & Bulirsch 2002 , Thm 3.6.24). Para un integrando que tiene 2 n derivadas continuas,

para algunos ξ en ( a , b ) , donde p n es el polinomio ortogonal mónico (es decir, el coeficiente principal es 1 ) de grado n y donde

En el caso especial importante de ω ( x ) = 1 , tenemos la estimación del error ( Kahaner, Moler & Nash 1989 , §5.2)
![{\ Displaystyle {\ frac {\ left (ba \ right) ^ {2n + 1} \ left (n! \ right) ^ {4}} {(2n + 1) \ left [\ left (2n \ right)! \ right] ^ {3}}} f ^ {(2n)} (\ xi), \ qquad a <\ xi <b.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55978744de6e75175beed299cc41fd11d8cdddc9)
Stoer y Bulirsch comentan que esta estimación de error es inconveniente en la práctica, ya que puede ser difícil estimar la derivada de orden 2 n y, además, el error real puede ser mucho menor que un límite establecido por la derivada. Otro enfoque consiste en utilizar dos reglas de cuadratura gaussianas de diferentes órdenes y estimar el error como la diferencia entre los dos resultados. Para este propósito, las reglas de cuadratura de Gauss-Kronrod pueden ser útiles.
Reglas de Gauss-Kronrod
Si se subdivide el intervalo [ a , b ] , los puntos de evaluación de Gauss de los nuevos subintervalos nunca coinciden con los puntos de evaluación anteriores (excepto en cero para los números impares), por lo que el integrando debe evaluarse en todos los puntos. Las reglas de Gauss-Kronrod son extensiones de las reglas de cuadratura de Gauss generadas al sumar n + 1 puntos a una regla de n puntos de tal manera que la regla resultante es de orden 2 n + 1 . Esto permite calcular estimaciones de orden superior mientras se reutilizan los valores de función de una estimación de orden inferior. La diferencia entre una regla de cuadratura de Gauss y su extensión de Kronrod se usa a menudo como una estimación del error de aproximación.
Reglas de Gauss-Lobatto
También conocida como cuadratura de Lobatto ( Abramowitz & Stegun 1972 , p. 888) , llamada así por el matemático holandés Rehuel Lobatto . Es similar a la cuadratura gaussiana con las siguientes diferencias:
error de harv: sin destino: CITEREFAbramowitzStegun1972 ( ayuda )
- Los puntos de integración incluyen los puntos finales del intervalo de integración.
- Es preciso para polinomios hasta grado 2 n - 3 , donde n es el número de puntos de integración ( Quarteroni, Sacco & Saleri 2000 ).
Cuadratura de Lobatto de la función f ( x ) en el intervalo [−1, 1] :
![{\ Displaystyle \ int _ {- 1} ^ {1} {f (x) \, dx} = {\ frac {2} {n (n-1)}} [f (1) + f (-1) ] + \ sum _ {i = 2} ^ {n-1} {w_ {i} f (x_ {i})} + R_ {n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/debe72ac248f8ae18af6b8814511b7068487ba24)
Abscisas: x i es el primer cero de , aquí denota el polinomio estándar de Legendre de m-ésimo grado y el guión denota la derivada.



Pesos:
![{\ Displaystyle w_ {i} = {\ frac {2} {n (n-1) \ left [P_ {n-1} \ left (x_ {i} \ right) \ right] ^ {2}}}, \ qquad x_ {i} \ neq \ pm 1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef48203f09833d6a365e378e786320cbca4938f7)
Recordatorio:
![{\ Displaystyle R_ {n} = {\ frac {-n \ left (n-1 \ right) ^ {3} 2 ^ {2n-1} \ left [\ left (n-2 \ right)! \ right] ^ {4}} {(2n-1) \ left [\ left (2n-2 \ right)! \ Right] ^ {3}}} f ^ {(2n-2)} (\ xi), \ qquad - 1 <\ xi <1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3958e99104629c7d8c85c193a735f2ddea4652db)
Algunos de los pesos son:
| Número de puntos, n
|
Puntos, x i
|
Pesos, w i
|

|
 |

|
 |

|

|
 |

|
 |

|

|
 |

|
 |

|
 |

|

|
 |

|
 |

|
 |

|

|
 |

|
 |

|
 |

|
 |

|
Una variante adaptativa de este algoritmo con 2 nodos interiores se encuentra en GNU Octave y MATLAB como quadly integrate.
Referencias
- Implementación de una solución precisa en cuadratura gaussiana generalizada para encontrar el campo elástico en un medio anisotrópico homogéneo
-
Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [junio de 1964]. "Capítulo 25.4, Integración". Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas . Serie de Matemáticas Aplicadas. 55 (Novena reimpresión con correcciones adicionales de la décima impresión original con correcciones (diciembre de 1972); primera ed.). Washington DC; Nueva York: Departamento de Comercio de los Estados Unidos, Oficina Nacional de Normas; Publicaciones de Dover. ISBN 978-0-486-61272-0. LCCN 64-60036 . Señor 0167642 . LCCN 65-12253 .
-
Anderson, Donald G. (1965). "Fórmulas de cuadratura gaussiana para "
 . Matemáticas. Comp . 19 (91): 477–481. doi : 10.1090 / s0025-5718-1965-0178569-1 .
. Matemáticas. Comp . 19 (91): 477–481. doi : 10.1090 / s0025-5718-1965-0178569-1 .
-
Golub, Gene H .; Welsch, John H. (1969), "Cálculo de las reglas de cuadratura de Gauss", Matemáticas de la computación , 23 (106): 221-230, doi : 10.1090 / S0025-5718-69-99647-1 , JSTOR 2004418
-
Gautschi, Walter (1968). "Construcción de fórmulas de cuadratura de Gauss-Christoffel". Matemáticas. Comp . 22 (102). págs. 251-270. doi : 10.1090 / S0025-5718-1968-0228171-0 . Señor 0228171 .
-
Gautschi, Walter (1970). "Sobre la construcción de reglas de cuadratura gaussianas a partir de momentos modificados". Matemáticas. Comp . 24 . págs. 245-260. doi : 10.1090 / S0025-5718-1970-0285117-6 . Señor 0285177 .
-
Piessens, R. (1971). "Fórmulas de cuadratura gaussiana para la integración numérica de la integral de Bromwich y la inversión de la transformada de Laplace". J. Eng. Matemáticas . 5 (1). págs. 1–9. Código bibliográfico : 1971JEnMa ... 5 .... 1P . doi : 10.1007 / BF01535429 .
-
Danloy, Bernard (1973). "Construcción numérica de fórmulas de cuadratura gaussiana para y ". Matemáticas. Comp . 27 (124). págs. 861–869. doi : 10.1090 / S0025-5718-1973-0331730-X . Señor 0331730 .


-
Kahaner, David; Moler, Cleve ; Nash, Stephen (1989), métodos numéricos y software , Prentice-Hall , ISBN 978-0-13-627258-8
-
Sagar, Robin P. (1991). "Una cuadratura gaussiana para el cálculo de integrales de Fermi-Dirac generalizadas". Computación. Phys. Comun . 66 (2-3): 271-275. Código bibliográfico : 1991CoPhC..66..271S . doi : 10.1016 / 0010-4655 (91) 90076-W .
-
Yakimiw, E. (1996). "Cálculo exacto de pesos en reglas clásicas de cuadratura de Gauss-Christoffel". J. Comput. Phys . 129 (2): 406–430. Código Bibliográfico : 1996JCoPh.129..406Y . doi : 10.1006 / jcph.1996.0258 .
-
Laurie, Dirk P. (1999), "Recuperación precisa de coeficientes de recursividad a partir de fórmulas de cuadratura gaussianas", J. Comput. Apl. Matemáticas. , 112 (1–2): 165–180, doi : 10.1016 / S0377-0427 (99) 00228-9
-
Laurie, Dirk P. (2001). "Cálculo de fórmulas de cuadratura tipo Gauss" . J. Comput. Apl. Matemáticas . 127 (1–2): 201–217. Código Bibliográfico : 2001JCoAM.127..201L . doi : 10.1016 / S0377-0427 (00) 00506-9 .
-
Riener, Cordian; Schweighofer, Markus (2018). "Aproximaciones de optimización a la cuadratura: Nuevas caracterizaciones de la cuadratura gaussiana en la línea y en cuadratura con pocos nodos en curvas algebraicas planas, en el plano y en dimensiones superiores". Revista de complejidad . 45 : 22–54. arXiv : 1607.08404 . doi : 10.1016 / j.jco.2017.10.002 .
-
Stoer, Josef; Bulirsch, Roland (2002), Introducción al análisis numérico (3.a ed.), Springer , ISBN 978-0-387-95452-3.
-
Temme, Nico M. (2010), "§3.5 (v): Cuadratura de Gauss" , en Olver, Frank WJ ; Lozier, Daniel M .; Boisvert, Ronald F .; Clark, Charles W. (eds.), Manual de funciones matemáticas del NIST , Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
-
Presione, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Sección 4.6. Cuadraturas gaussianas y polinomios ortogonales" , Recetas numéricas: El arte de la informática científica (3ª ed.), Nueva York: Cambridge University Press, ISBN 978-0-521-88068-8
-
Gil, Amparo; Segura, Javier; Temme, Nico M. (2007), "§5.3: Cuadratura de Gauss", Métodos numéricos para funciones especiales , SIAM, ISBN 978-0-89871-634-4
-
Quarteroni, Alfio; Sacco, Riccardo; Saleri, Fausto (2000). Matemáticas numéricas . Nueva York: Springer-Verlag . págs. 422 , 425. ISBN 0-387-98959-5.
- Walter Gautschi: "Un repositorio de software para cuadraturas gaussianas y funciones de Christoffel", SIAM, ISBN 978-1-611976-34-2 (2020).
- Específico
-
^ Methodus nova integralium valores por aproximationem inveniendi. En: Com. Soc. Sci. Göttingen Math. Band 3, 1815, S. 29–76, Gallica , datiert 1814, auch in Werke, Band 3, 1876, S. 163–196.
-
^ CGJ Jacobi : Ueber Gauß 'neue Methode, die Werthe der Integrale näherungsweise zu finden. En: Journal für Reine und Angewandte Mathematik. Band 1, 1826, S. 301-308, (en línea) , und Werke, Band 6.
-
^ Gander, Walter; Gautschi, Walter (2000). "Cuadratura adaptativa - revisada" . BIT Matemáticas numéricas . 40 (1): 84–101. doi : 10.1023 / A: 1022318402393 .
-
^ "Integración numérica - integral de MATLAB" .
-
^ "Funciones de una variable (octava GNU)" . Consultado el 28 de septiembre de 2018 .
enlaces externos
-
"Fórmula de cuadratura de Gauss" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
-
ALGLIB contiene una colección de algoritmos para la integración numérica (en C # / C ++ / Delphi / Visual Basic / etc.)
-
Biblioteca científica GNU : incluye la versión C de los algoritmos QUADPACK (consulte también Biblioteca científica GNU )
- De la cuadratura de Lobatto a la constante de Euler e
-
Regla de integración de cuadratura gaussiana: notas, PPT, Matlab, Mathematica, Maple, Mathcad en el Instituto de métodos numéricos holísticos
- Weisstein, Eric W. "Cuadratura Legendre-Gauss" . MathWorld .
-
Cuadratura gaussiana por Chris Maes y Anton Antonov, Wolfram Demonstrations Project .
-
Pesos tabulados y abscisas con código fuente de Mathematica , alta precisión (16 y 256 decimales) Pesos en cuadratura y abscisas de Legendre-Gauss, para n = 2 a n = 64, con código fuente Mathematica.
-
Código fuente de Mathematica distribuido bajo GNU LGPL para abscisas y generación de pesos para funciones de ponderación arbitrarias W (x), dominios de integración y precisiones.
- Cuadratura gaussiana en Boost.Math, para precisión arbitraria y orden de aproximación
- Cuadratura Gauss-Kronrod en Boost.Math
- Nodos y pesos de la cuadratura gaussiana













![[-1, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
![{\ Displaystyle w_ {i} = {\ frac {2} {\ left (1-x_ {i} ^ {2} \ right) \ left [P '_ {n} (x_ {i}) \ right] ^ {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92a5533b3b5d42f1c60c3c5e6e5d62c37c2878a3)



































































































































![{\ Displaystyle {\ frac {\ left (ba \ right) ^ {2n + 1} \ left (n! \ right) ^ {4}} {(2n + 1) \ left [\ left (2n \ right)! \ right] ^ {3}}} f ^ {(2n)} (\ xi), \ qquad a <\ xi <b.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55978744de6e75175beed299cc41fd11d8cdddc9)
![{\ Displaystyle \ int _ {- 1} ^ {1} {f (x) \, dx} = {\ frac {2} {n (n-1)}} [f (1) + f (-1) ] + \ sum _ {i = 2} ^ {n-1} {w_ {i} f (x_ {i})} + R_ {n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/debe72ac248f8ae18af6b8814511b7068487ba24)



![{\ Displaystyle w_ {i} = {\ frac {2} {n (n-1) \ left [P_ {n-1} \ left (x_ {i} \ right) \ right] ^ {2}}}, \ qquad x_ {i} \ neq \ pm 1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef48203f09833d6a365e378e786320cbca4938f7)
![{\ Displaystyle R_ {n} = {\ frac {-n \ left (n-1 \ right) ^ {3} 2 ^ {2n-1} \ left [\ left (n-2 \ right)! \ right] ^ {4}} {(2n-1) \ left [\ left (2n-2 \ right)! \ Right] ^ {3}}} f ^ {(2n-2)} (\ xi), \ qquad - 1 <\ xi <1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3958e99104629c7d8c85c193a735f2ddea4652db)





























