Prueba de razón - Ratio test

En matemáticas , la prueba de razón es una prueba (o "criterio") para la convergencia de una serie.

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} a_ {n},}$

donde cada término es un número real o complejo y una _n es distinta de cero cuando n es grande. La prueba fue publicada por primera vez por Jean le Rond d'Alembert y a veces se la conoce como prueba de proporción de d'Alembert o prueba de proporción de Cauchy .

La prueba

Diagrama de decisión para la prueba de razón

La forma habitual de la prueba hace uso del límite

${\ Displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |.}$

( 1 )

La prueba de razón establece que:

• si L <1 entonces la serie converge absolutamente ;
• si L > 1 entonces la serie es divergente ;
• si L = 1 o el límite no existe, entonces la prueba no es concluyente, porque existen series convergentes y divergentes que satisfacen este caso.

Es posible hacer que la prueba de relación sea aplicable a ciertos casos en los que el límite L no existe, si se utilizan límite superior y límite inferior . Los criterios de la prueba también se pueden refinar para que la prueba sea a veces concluyente incluso cuando L = 1. Más específicamente, sea

${\ Displaystyle R = \ lim \ sup \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$

${\ Displaystyle r = \ lim \ inf \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$.

Entonces la prueba de razón establece que:

• si R <1, la serie converge absolutamente;
• si r > 1, la serie diverge;
• si para todo n grande (independientemente del valor de r ), la serie también diverge; esto se debe a que es distinto de cero y creciente y, por lo tanto, una _n no se acerca a cero;${\ Displaystyle \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | \ geq 1}$${\ Displaystyle | a_ {n} |}$
• de lo contrario, la prueba no es concluyente.

Si existe el límite L en ( 1 ), debemos tener L = R = r . Entonces, la prueba de relación original es una versión más débil de la refinada.

Ejemplos de

Convergente porque L <1

Considere la serie

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {n} {e ^ {n}}}}$

Aplicando la prueba de razón, se calcula el límite

${\ Displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | = \ lim _ {n \ to \ infty} \ left | {\ frac {\ frac {n + 1} {e ^ {n + 1}}} {\ frac {n} {e ^ {n}}}} \ right | = {\ frac {1} { e}} <1.}$

Dado que este límite es menor que 1, la serie converge.

Divergente porque L > 1

Considere la serie

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {e ^ {n}} {n}}.}$

Poniendo esto en la prueba de proporción:

${\ Displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | = \ lim _ {n \ to \ infty} \ left | {\ frac {\ frac {e ^ {n + 1}} {n + 1}} {\ frac {e ^ {n}} {n}}} \ right | = e> 1.}$

Por tanto, la serie diverge.

No concluyente porque L = 1

Considere las tres series

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} 1,}$

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {n ^ {2}}},}$

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {(-1) ^ {n + 1}} {n}}.}$

La primera serie ( 1 + 1 + 1 + 1 + ⋯ ) diverge, la segunda (la central del problema de Basilea ) converge absolutamente y la tercera (la serie armónica alterna ) converge condicionalmente. Sin embargo, las razones de magnitud término por término de las tres series son respectivamente    y    . Entonces, en los tres casos, se tiene que el límite es igual a 1. Esto ilustra que cuando L = 1, la serie puede converger o divergir y, por lo tanto, la prueba de razón original no es concluyente. En tales casos, se requieren pruebas más refinadas para determinar la convergencia o divergencia. ${\ Displaystyle \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$${\ Displaystyle 1,}$   ${\ Displaystyle {\ frac {n ^ {2}} {(n + 1) ^ {2}}}}$${\ Displaystyle {\ frac {n} {n + 1}}}$${\ Displaystyle \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right |}$

Prueba

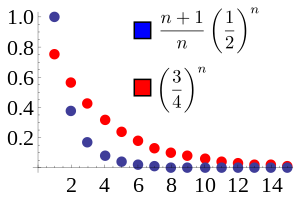
En este ejemplo, la proporción de términos adyacentes en la secuencia azul converge a L = 1/2. Elegimos r  = (L + 1) / 2 = 3/4. Entonces, la secuencia azul está dominada por la secuencia roja r ^k para todo n ≥ 2. La secuencia roja converge, por lo que la secuencia azul también lo hace.

A continuación se muestra una prueba de la validez de la prueba de relación original.

Supongamos eso . Entonces podemos mostrar que la serie converge absolutamente al mostrar que sus términos eventualmente serán menores que los de una cierta serie geométrica convergente . Para hacer esto, considere un número real r tal que . Esto implica que para n suficientemente grande ; decir, para todos n mayor que N . Por tanto, para cada n > N e i > 0, y así ${\ Displaystyle L = \ lim _ {n \ to \ infty} \ left | {\ frac {a_ {n + 1}} {a_ {n}}} \ right | <1}$ ${\ Displaystyle L <r <1}$${\ Displaystyle | a_ {n + 1} | <r | a_ {n} |}$${\ Displaystyle | a_ {n + i} | <r ^ {i} | a_ {n} |}$

${\ Displaystyle \ sum _ {i = N + 1} ^ {\ infty} | a_ {i} | = \ sum _ {i = 1} ^ {\ infty} \ left | a_ {N + i} \ right | <\ sum _ {i = 1} ^ {\ infty} r ^ {i} | a_ {N} | = | a_ {N} | \ sum _ {i = 1} ^ {\ infty} r ^ {i} = | a_ {N} | {\ frac {r} {1-r}} <\ infty.}$

Es decir, la serie converge absolutamente.

Por otro lado, si L > 1, entonces para n suficientemente grande , de modo que el límite de los sumandos sea distinto de cero. Por tanto, la serie diverge. ${\ Displaystyle | a_ {n + 1} |> | a_ {n} |}$

Extensiones para L = 1

Como se vio en el ejemplo anterior, la prueba de razón puede no ser concluyente cuando el límite de la razón es 1. Sin embargo, las extensiones a la prueba de razón permiten a veces lidiar con este caso.

En todas las pruebas siguientes, se supone que Σ a _n es una suma con a _n positivo . Estas pruebas también se pueden aplicar a cualquier serie con un número finito de términos negativos. Cualquiera de estas series puede escribirse como:

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} a_ {n} = \ sum _ {n = 1} ^ {N} a_ {n} + \ sum _ {n = N + 1} ^ { \ infty} a_ {n}}$

donde una _N es el término negativo con el índice más alto. La primera expresión de la derecha es una suma parcial que será finita, por lo que la convergencia de toda la serie estará determinada por las propiedades de convergencia de la segunda expresión de la derecha, que puede volver a indexarse ​​para formar una serie de todos términos positivos que comienzan en n = 1.

Cada prueba define un parámetro de prueba (ρ _n ) que especifica el comportamiento de ese parámetro necesario para establecer convergencia o divergencia. Para cada prueba, existe una forma más débil de la prueba que, en cambio, impondrá restricciones sobre lim _{n-> ∞} ρ _n .

Todas las pruebas tienen regiones en las que no describen las propiedades de convergencia de Σa _n . De hecho, ninguna prueba de convergencia puede describir completamente las propiedades de convergencia de la serie. Esto se debe a que si Σa _n es convergente, se puede encontrar una segunda serie convergente Σb _n que converge más lentamente: es decir, tiene la propiedad de que lim _{n-> ∞} (b _n / a _n ) = ∞. Además, si Σa _n es divergente, se puede encontrar una segunda serie divergente Σb _n que diverge más lentamente: es decir, tiene la propiedad de que lim _{n-> ∞} (b _n / a _n ) = 0. Las pruebas de convergencia utilizan esencialmente la comparación prueba en alguna familia particular de _n , y falla en secuencias que convergen o divergen más lentamente.

Jerarquía de De Morgan

Augustus De Morgan propuso una jerarquía de pruebas de tipo proporcional

Los parámetros de la prueba de relación ( ) a continuación generalmente involucran todos los términos del formulario . Este término se puede multiplicar por para ceder . Este término puede reemplazar al término anterior en la definición de los parámetros de prueba y las conclusiones extraídas seguirán siendo las mismas. Por consiguiente, no se hará ninguna distinción entre las referencias que utilizan una u otra forma del parámetro de prueba. ${\ Displaystyle \ rho _ {n}}$${\ Displaystyle D_ {n} a_ {n} / a_ {n + 1} -D_ {n + 1}}$${\ Displaystyle a_ {n + 1} / a_ {n}}$${\ Displaystyle D_ {n} -D_ {n + 1} a_ {n + 1} / a_ {n}}$

1. Prueba de la relación de d'Alembert

La primera prueba en la jerarquía de De Morgan es la prueba de razón como se describe arriba.

2. Prueba de Raabe

Esta extensión se debe a Joseph Ludwig Raabe . Definir:

${\ Displaystyle \ rho _ {n} \ equiv n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right)}$

(y algunos términos adicionales, consulte Ali, Blackburn, Feld, Duris (ninguno), Duris2)

La serie:

• Converge cuando existe un c> 1 de tal manera que para todos n> N .${\ Displaystyle \ rho _ {n} \ geq c}$
• Diverge cuando para todos n> N .${\ Displaystyle \ rho _ {n} \ leq 1}$
• De lo contrario, la prueba no es concluyente.

Para la versión límite, la serie:

• Converge si (esto incluye el caso ρ = ∞)${\ Displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}> 1}$
• Diverge si .${\ Displaystyle \ lim _ {n \ to \ infty} \ rho _ {n} <1}$
• Si ρ = 1, la prueba no es concluyente.

Cuando el límite anterior no existe, es posible utilizar límites superiores e inferiores. La serie:

• Converger si ${\ Displaystyle \ liminf _ {n \ to \ infty} \ rho _ {n}> 1}$
• Diverge si ${\ Displaystyle \ limsup _ {n \ rightarrow \ infty} \ rho _ {n} <1}$
• De lo contrario, la prueba no es concluyente.

Prueba de la prueba de Raabe

Definiendo , no necesitamos asumir que el límite existe; si , entonces diverge, mientras que si la suma converge. ${\ Displaystyle \ rho _ {n} \ equiv n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right)}$${\ Displaystyle \ limsup \ rho _ {n} <1}$${\ Displaystyle \ sum a_ {n}}$${\ Displaystyle \ liminf \ rho _ {n}> 1}$

La prueba procede esencialmente por comparación con . Supongamos primero eso . Por supuesto, si entonces es grande , entonces la suma diverge; asume entonces eso . Existe tal que para todos , es decir . Por lo tanto , lo que implica que para ; ya que esto demuestra que diverge. ${\ Displaystyle \ sum 1 / n ^ {R}}$${\ Displaystyle \ limsup \ rho _ {n} <1}$${\ Displaystyle \ limsup \ rho _ {n} <0}$${\ Displaystyle a_ {n + 1} \ geq a_ {n}}$${\ Displaystyle n}$${\ Displaystyle 0 \ leq \ limsup \ rho _ {n} <1}$${\ Displaystyle R <1}$${\ Displaystyle \ rho _ {n} \ leq R}$${\ Displaystyle n \ geq N}$${\ Displaystyle a_ {n} / a_ {n + 1} \ leq \ left (1 + {\ frac {R} {n}} \ right) \ leq e ^ {R / n}}$${\ Displaystyle a_ {n + 1} \ geq a_ {n} e ^ {- R / n}}$${\ Displaystyle a_ {n + 1} \ geq a_ {N} e ^ {- R (1 / N + \ dots + 1 / n)} \ geq ca_ {N} e ^ {- R \ log (n)} = ca_ {N} / n ^ {R}}$${\ Displaystyle n \ geq N}$${\ Displaystyle R <1}$${\ Displaystyle \ sum a_ {n}}$

La prueba de la otra mitad es completamente análoga, con la mayoría de las desigualdades simplemente invertidas. Necesitamos una desigualdad preliminar para usar en lugar de la simple que se usó anteriormente: Fix y . Tenga en cuenta eso . Entonces ; de ahí . ${\ Displaystyle 1 + t <e ^ {t}}$${\ Displaystyle R}$${\ Displaystyle N}$${\ Displaystyle \ log \ left (1 + {\ frac {R} {n}} \ right) = {\ frac {R} {n}} + O \ left ({\ frac {1} {n ^ {2 }}}\Derecha)}$${\ Displaystyle \ log \ left (\ left (1 + {\ frac {R} {N}} \ right) \ dots \ left (1 + {\ frac {R} {n}} \ right) \ right) = R \ left ({\ frac {1} {N}} + \ dots + {\ frac {1} {n}} \ right) + O (1) = R \ log (n) + O (1)}$${\ Displaystyle \ left (1 + {\ frac {R} {N}} \ right) \ dots \ left (1 + {\ frac {R} {n}} \ right) \ geq cn ^ {R}}$

Supongamos ahora eso . Argumentando como en el primer párrafo, utilizando la desigualdad establecida en el párrafo anterior, vemos que existe tal que para ; ya que esto demuestra que converge. ${\ Displaystyle \ liminf \ rho _ {n}> 1}$${\ Displaystyle R> 1}$${\ Displaystyle a_ {n + 1} \ leq ca_ {N} n ^ {- R}}$${\ Displaystyle n \ geq N}$${\ Displaystyle R> 1}$${\ Displaystyle \ sum a_ {n}}$

3. Prueba de Bertrand

Esta extensión se debe a Joseph Bertrand y Augustus De Morgan .

Definiendo:

${\ Displaystyle \ rho _ {n} \ equiv n \ ln n \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) - \ ln n}$

La prueba de Bertrand afirma que la serie:

• Converge cuando existe un c> 1 de tal manera que para todos n> N .${\ Displaystyle \ rho _ {n} \ geq c}$
• Diverge cuando para todos n> N .${\ Displaystyle \ rho _ {n} \ leq 1}$
• De lo contrario, la prueba no es concluyente.

Para la versión límite, la serie:

• Converge si (esto incluye el caso ρ = ∞)${\ Displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}> 1}$
• Diverge si .${\ Displaystyle \ lim _ {n \ to \ infty} \ rho _ {n} <1}$
• Si ρ = 1, la prueba no es concluyente.

Cuando el límite anterior no existe, es posible utilizar límites superiores e inferiores. La serie:

• Converger si ${\ Displaystyle \ liminf \ rho _ {n}> 1}$
• Diverge si ${\ Displaystyle \ limsup \ rho _ {n} <1}$
• De lo contrario, la prueba no es concluyente.

4. Prueba de Bertrand ampliada

Esta extensión probablemente apareció por primera vez por Margaret Martin en. Se proporciona una prueba breve basada en la prueba de Kummer y sin supuestos técnicos (como la existencia de los límites, por ejemplo).

Dejado ser un número entero, y dejar que denotan la ésimo iterate de logaritmo natural , es decir, y para cualquier , . ${\ Displaystyle K \ geq 1}$${\ Displaystyle \ ln _ {(K)} (x)}$${\ Displaystyle K}$${\ Displaystyle \ ln _ {(1)} (x) = \ ln (x)}$${\ Displaystyle 2 \ leq k \ leq K}$${\ Displaystyle \ ln _ {(k)} (x) = \ ln _ {(k-1)} (\ ln (x))}$

Suponga que la razón , cuando es grande, se puede presentar en la forma ${\ Displaystyle a_ {n} / a_ {n + 1}}$${\ Displaystyle n}$

${\ Displaystyle {\ frac {a_ {n}} {a_ {n + 1}}} = 1 + {\ frac {1} {n}} + {\ frac {1} {n}} \ sum _ {i = 1} ^ {K-1} {\ frac {1} {\ prod _ {k = 1} ^ {i} \ ln _ {(k)} (n)}} + {\ frac {\ rho _ { n}} {n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n)}}, \ quad K \ geq 1.}$

(Se supone que la suma vacía es 0. Con , la prueba se reduce a la prueba de Bertrand). ${\ Displaystyle K = 1}$

El valor se puede presentar explícitamente en la forma ${\ Displaystyle \ rho _ {n}}$

${\ Displaystyle \ rho _ {n} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) \ left ({\ frac {a_ {n}} {a_ {n +1}}} - 1 \ derecha) - \ sum _ {j = 1} ^ {K} \ prod _ {k = 1} ^ {j} \ ln _ {(K-k + 1)} (n) .}$

La prueba extendida de Bertrand afirma que la serie

• Convergen cuando existe tal que para todos .${\ Displaystyle c> 1}$${\ Displaystyle \ rho _ {n} \ geq c}$${\ Displaystyle n> N}$
• Diverge cuando para todos .${\ Displaystyle \ rho _ {n} \ leq 1}$${\ Displaystyle n> N}$
• De lo contrario, la prueba no es concluyente.

Para la versión límite, la serie

• Converge si (esto incluye el caso )${\ Displaystyle \ rho = \ lim _ {n \ to \ infty} \ rho _ {n}> 1}$${\ Displaystyle \ rho = \ infty}$
• Diverge si .${\ Displaystyle \ lim _ {n \ to \ infty} \ rho _ {n} <1}$
• Si , la prueba no es concluyente.${\ Displaystyle \ rho = 1}$

Cuando el límite anterior no existe, es posible utilizar límites superiores e inferiores. Las series

• Converger si ${\ Displaystyle \ liminf \ rho _ {n}> 1}$
• Diverge si ${\ Displaystyle \ limsup \ rho _ {n} <1}$
• De lo contrario, la prueba no es concluyente.

Para conocer las aplicaciones de la prueba de Bertrand ampliada, consulte el proceso de nacimiento-muerte .

5. Prueba de Gauss

Esta ampliación se debe a Carl Friedrich Gauss .

Suponiendo que a _n > 0 y r> 1 , si se puede encontrar una secuencia acotada C _n tal que para todo n :

${\ Displaystyle {\ frac {a_ {n}} {a_ {n + 1}}} = 1 + {\ frac {\ rho} {n}} + {\ frac {C_ {n}} {n ^ {r }}}}$

entonces la serie:

• Converger si ${\ Displaystyle \ rho> 1}$
• Diverge si ${\ Displaystyle \ rho \ leq 1}$

6. Prueba de Kummer

Esta extensión se debe a Ernst Kummer .

Sea ζ _n una secuencia auxiliar de constantes positivas. Definir

${\ Displaystyle \ rho _ {n} \ equiv \ left (\ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1} \ right) }$

La prueba de Kummer establece que la serie:

• Converge si existe tal que para todo n> N. (Tenga en cuenta que esto no es lo mismo que decir )${\ Displaystyle c> 0}$${\ Displaystyle \ rho _ {n} \ geq c}$${\ Displaystyle \ rho _ {n}> 0}$
• Diverge si para todo n> N y diverge.${\ Displaystyle \ rho _ {n} \ leq 0}$${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} 1 / \ zeta _ {n}}$

Para la versión límite, la serie:

• Converge si (esto incluye el caso ρ = ∞)${\ Displaystyle \ lim _ {n \ to \ infty} \ rho _ {n}> 0}$
• Diverge si y diverge.${\ Displaystyle \ lim _ {n \ to \ infty} \ rho _ {n} <0}$${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} 1 / \ zeta _ {n}}$
• De lo contrario, la prueba no es concluyente.

Cuando el límite anterior no existe, es posible utilizar límites superiores e inferiores. La serie

• Converger si ${\ Displaystyle \ liminf _ {n \ to \ infty} \ rho _ {n}> 0}$
• Diverge si y diverge.${\ Displaystyle \ limsup _ {n \ to \ infty} \ rho _ {n} <0}$${\ Displaystyle \ sum 1 / \ zeta _ {n}}$

Casos especiales

Todas las pruebas en la jerarquía de De Morgan, excepto la prueba de Gauss, pueden verse fácilmente como casos especiales de la prueba de Kummer:

• Para la prueba de razón, sea ζ _n = 1. Luego:

${\ Displaystyle \ rho _ {Kummer} = \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) = 1 / \ rho _ {Ratio} -1}$

• Para la prueba de Raabe, sea ζ _n = n. Luego:

${\ Displaystyle \ rho _ {Kummer} = \ left (n {\ frac {a_ {n}} {a_ {n + 1}}} - (n + 1) \ right) = \ rho _ {Raabe} -1 }$

• Para la prueba de Bertrand, sea ζ _n = n ln (n). Luego:

${\ Displaystyle \ rho _ {Kummer} = n \ ln (n) \ left ({\ frac {a_ {n}} {a_ {n + 1}}} \ right) - (n + 1) \ ln (n +1)}$

El uso y la aproximación para n grande , que es insignificante en comparación con los otros términos, se puede escribir: ${\ Displaystyle \ ln (n + 1) = \ ln (n) + \ ln (1 + 1 / n)}$ ${\ Displaystyle \ ln (1 + 1 / n) \ rightarrow 1 / n}$${\ Displaystyle \ rho _ {Kummer}}$

${\ Displaystyle \ rho _ {Kummer} = n \ ln (n) \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) - \ ln (n) -1 = \ rho _ {Bertrand} -1}$

• Para la prueba de Bertrand extendida, supongamos que De la expansión de la serie de Taylor para grandes llegamos a la aproximación${\ Displaystyle \ zeta _ {n} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n).}$${\ Displaystyle n}$

${\ Displaystyle \ ln _ {(k)} (n + 1) = \ ln _ {(k)} (n) + {\ frac {1} {n \ prod _ {j = 1} ^ {k-1 } \ ln _ {(j)} (n)}} + O \ left ({\ frac {1} {n ^ {2}}} \ right),}$

donde se supone que el producto vacío es 1. Entonces,

${\ Displaystyle \ rho _ {Kummer} = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) {\ frac {a_ {n}} {a_ {n + 1} }} - (n + 1) \ left [\ prod _ {k = 1} ^ {K} \ left (\ ln _ {(k)} (n) + {\ frac {1} {n \ prod _ { j = 1} ^ {k-1} \ ln _ {(j)} (n)}} \ derecha) \ derecha] + o (1) = n \ prod _ {k = 1} ^ {K} \ ln _ {(k)} (n) \ left ({\ frac {a_ {n}} {a_ {n + 1}}} - 1 \ right) - \ sum _ {j = 1} ^ {K} \ prod _ {k = 1} ^ {j} \ ln _ {(K-k + 1)} (n) -1 + o (1).}$

Por eso,

${\ Displaystyle \ rho _ {Kummer} = \ rho _ {ExtendedBertrand} -1.}$

Tenga en cuenta que para estas cuatro pruebas, cuanto más alto están en la jerarquía de De Morgan, más lentamente diverge la serie. ${\ Displaystyle 1 / \ zeta _ {n}}$

Prueba de la prueba de Kummer

Si entonces fija un número positivo . Existe un número natural tal que para cada${\ Displaystyle \ rho _ {n}> 0}$${\ Displaystyle 0 <\ delta <\ rho _ {n}}$${\ Displaystyle N}$${\ Displaystyle n> N,}$

${\ Displaystyle \ delta \ leq \ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1}.}$

Ya que , para cada${\ Displaystyle a_ {n + 1}> 0}$${\ Displaystyle n> N,}$

${\ Displaystyle 0 \ leq \ delta a_ {n + 1} \ leq \ zeta _ {n} a_ {n} - \ zeta _ {n + 1} a_ {n + 1}.}$

En particular para todos, lo que significa que a partir del índice la secuencia es monótonamente decreciente y positiva, lo que en particular implica que está delimitada por debajo de 0. Por lo tanto, el límite ${\ Displaystyle \ zeta _ {n + 1} a_ {n + 1} \ leq \ zeta _ {n} a_ {n}}$${\ Displaystyle n \ geq N}$${\ Displaystyle N}$${\ Displaystyle \ zeta _ {n} a_ {n}> 0}$

${\ Displaystyle \ lim _ {n \ to \ infty} \ zeta _ {n} a_ {n} = L}$ existe.

Esto implica que la serie telescópica positiva

${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} \ left (\ zeta _ {n} a_ {n} - \ zeta _ {n + 1} a_ {n + 1} \ right)}$ es convergente,

y ya que para todos ${\ Displaystyle n> N,}$

${\ Displaystyle \ delta a_ {n + 1} \ leq \ zeta _ {n} a_ {n} - \ zeta _ {n + 1} a_ {n + 1}}$

según la prueba de comparación directa para series positivas, la serie es convergente. ${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} \ delta a_ {n + 1}}$

Por otro lado, si , entonces hay un N tal que aumenta para . En particular, existe un para el cual para todos y, por lo tanto, difiere en comparación con . ${\ Displaystyle \ rho <0}$${\ Displaystyle \ zeta _ {n} a_ {n}}$${\ Displaystyle n> N}$${\ Displaystyle \ epsilon> 0}$${\ Displaystyle \ zeta _ {n} a_ {n}> \ epsilon}$${\ Displaystyle n> N}$${\ Displaystyle \ sum _ {n} a_ {n} = \ sum _ {n} {\ frac {a_ {n} \ zeta _ {n}} {\ zeta _ {n}}}}$${\ Displaystyle \ sum _ {n} {\ frac {\ epsilon} {\ zeta _ {n}}}}$

Modificación de Tong de la prueba de Kummer

Tong estableció una nueva versión de la prueba de Kummer. Consulte también para más discusiones y nuevas pruebas. La modificación proporcionada del teorema de Kummer caracteriza todas las series positivas, y la convergencia o divergencia se puede formular en forma de dos condiciones necesarias y suficientes, una para la convergencia y otra para la divergencia.

• La serie converge si y sólo si existe una secuencia positiva , de tal manera que${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} a_ {n}}$${\ Displaystyle \ zeta _ {n}}$${\ Displaystyle n = 1,2, \ dots}$${\ Displaystyle \ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1} \ geq c> 0.}$

• La serie diverge si y sólo si existe una secuencia positiva , de tal manera que y${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} a_ {n}}$${\ Displaystyle \ zeta _ {n}}$${\ Displaystyle n = 1,2, \ dots}$${\ Displaystyle \ zeta _ {n} {\ frac {a_ {n}} {a_ {n + 1}}} - \ zeta _ {n + 1} \ leq 0,}$${\ Displaystyle \ sum _ {n = 1} ^ {\ infty} {\ frac {1} {\ zeta _ {n}}} = \ infty.}$

Segunda prueba de relación de Ali

Una prueba de razón más refinada es la segunda prueba de razón: Para definir: ${\ Displaystyle a_ {n}> 0}$

${\ Displaystyle L_ {0} \ equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}}}}$

${\ Displaystyle L_ {1} \ equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$

${\ Displaystyle L \ equiv \ max (L_ {0}, L_ {1})}$

Según la segunda prueba de proporción, la serie:

• Converger si ${\ Displaystyle L <{\ frac {1} {2}}}$
• Diverge si ${\ Displaystyle L> {\ frac {1} {2}}}$
• Si entonces la prueba no es concluyente.${\ Displaystyle L = {\ frac {1} {2}}}$

Si los límites anteriores no existen, es posible utilizar los límites superior e inferior. Definir:

${\ Displaystyle L_ {0} \ equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}}}}$		${\ Displaystyle L_ {1} \ equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$
${\ Displaystyle \ ell _ {0} \ equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n}} {a_ {n}}}}$		${\ Displaystyle \ ell _ {1} \ equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {2n + 1}} {a_ {n}}}}$
${\ Displaystyle L \ equiv \ max (L_ {0}, L_ {1})}$		${\ Displaystyle \ ell \ equiv \ min (\ ell _ {0}, \ ell _ {1})}$

Entonces la serie:

• Converger si ${\ Displaystyle L <{\ frac {1} {2}}}$
• Diverge si ${\ Displaystyle \ ell> {\ frac {1} {2}}}$
• Si entonces la prueba no es concluyente.${\ Displaystyle \ ell \ leq {\ frac {1} {2}} \ leq L}$

Prueba de la relación de Ali${\ Displaystyle m}$

Esta prueba es una extensión directa de la segunda prueba de razón. Para una definición positiva : ${\ Displaystyle 0 \ leq k \ leq m-1,}$${\ Displaystyle a_ {n}}$

${\ Displaystyle L_ {k} \ equiv \ lim _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$

${\ Displaystyle L \ equiv \ max (L_ {0}, L_ {1}, \ ldots, L_ {m-1})}$

Según la prueba de relación, la serie: ${\ Displaystyle m}$

• Converger si ${\ Displaystyle L <{\ frac {1} {m}}}$
• Diverge si ${\ Displaystyle L> {\ frac {1} {m}}}$
• Si entonces la prueba no es concluyente.${\ Displaystyle L = {\ frac {1} {m}}}$

Si los límites anteriores no existen, es posible utilizar los límites superior e inferior. Para definir: ${\ Displaystyle 0 \ leq k \ leq m-1}$

${\ Displaystyle L_ {k} \ equiv \ limsup _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$
${\ Displaystyle \ ell _ {k} \ equiv \ liminf _ {n \ rightarrow \ infty} {\ frac {a_ {mn + k}} {a_ {n}}}}$
${\ Displaystyle L \ equiv \ max (L_ {0}, L_ {1}, \ ldots, L_ {m-1})}$		${\ Displaystyle \ ell \ equiv \ min (\ ell _ {0}, \ ell _ {1}, \ ldots, \ ell _ {m-1})}$

Entonces la serie:

• Converger si ${\ Displaystyle L <{\ frac {1} {m}}}$
• Diverge si ${\ Displaystyle \ ell> {\ frac {1} {m}}}$
• Si , entonces la prueba no es concluyente.${\ Displaystyle \ ell \ leq {\ frac {1} {m}} \ leq L}$

Prueba de relación de Ali-Deutsche Cohen${\ Displaystyle \ varphi}$

Esta prueba es una extensión de la prueba de relación. ${\ Displaystyle m}$

Suponga que la secuencia es una secuencia decreciente positiva. ${\ Displaystyle a_ {n}}$

Sea tal que exista. Denotar y asumir . ${\ Displaystyle \ varphi: \ mathbb {Z} ^ {+} \ to \ mathbb {Z} ^ {+}}$${\ Displaystyle \ lim _ {n \ to \ infty} {\ frac {n} {\ varphi (n)}}}$${\ Displaystyle \ alpha = \ lim _ {n \ to \ infty} {\ frac {n} {\ varphi (n)}}}$${\ Displaystyle 0 <\ alpha <1}$

Suponga también que ${\ Displaystyle \ lim _ {n \ to \ infty} {\ frac {a _ {\ varphi (n)}} {a_ {n}}} = L.}$

Entonces la serie:

• Converger si ${\ Displaystyle L <\ alpha}$
• Diverge si ${\ Displaystyle \ ell> \ alpha}$
• Si , entonces la prueba no es concluyente.${\ Displaystyle L = \ alpha}$

Ver también

• Prueba de raíz
• Radio de convergencia

Notas al pie

Referencias

• d'Alembert, J. (1768), Opuscules , V , págs. 171-183.
• Apostol, Tom M. (1974), Análisis matemático (2a ed.), Addison-Wesley , ISBN 978-0-201-00288-1: §8.14.
• Knopp, Konrad (1956), Infinite Sequences and Series , Nueva York: Dover Publications, Bibcode : 1956iss..book ..... K , ISBN 978-0-486-60153-3: §3.3, 5.4.
• Rudin, Walter (1976), Principios del análisis matemático (3.a ed.), Nueva York: McGraw-Hill, Inc., ISBN 978-0-07-054235-8: §3.34.
• "Criterio de Bertrand" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• "Criterio de Gauss" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• "Criterio de Kummer" , Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Watson, GN; Whittaker, ET (1963), Un curso de análisis moderno (4a ed.), Cambridge University Press, ISBN 978-0-521-58807-2: §2.36, 2.37.