Mecánica de contacto - Contact mechanics

Parte de una serie sobre
Mecánica de Medios Continuos
:${\ Displaystyle J = -D {\ frac {d \ varphi} {dx}}}$ Leyes de difusión de Fick
Leyes Conservaciones Masa Impulso Energía Desigualdades Clausius – Duhem (entropía)
Mecánica de sólidos Deformación Elasticidad lineal Plasticidad ley de Hooke Estrés Deformación finita Tensión infinitesimal Compatibilidad Doblado Mecánicos de contacto friccional Teoría de fallas materiales Mecánica de fracturas
Mecánica de fluidos Fluidos Estática  · Dinámica Principio de Arquímedes  · Principio de Bernoulli Ecuaciones de Navier-Stokes Ecuación de Poiseuille  · Ley de Pascal Viscosidad ( Newtoniano  · no newtoniano ) Flotabilidad  · Mezcla  · Presión Liquidos Tensión superficial Acción capilar Gases Atmósfera Ley de Boyle Ley de Charles Ley combinada de los gases Ley de Fick Ley de Gay-Lussac Ley de graham Plasma
Reología Viscoelasticidad Reometría Reómetro Fluidos inteligentes Electrorreológico Magnetorreológico Ferrofluidos
Científicos Bernoulli Boyle Cauchy Charles Euler Fick Gay-Lussac Graham Hooke Newton Navier Noll Pascal Stokes Truesdell
v t mi

La mecánica de contacto es el estudio de la deformación de sólidos que se tocan entre sí en uno o más puntos. Una distinción central en la mecánica de contacto es entre las tensiones que actúan perpendicularmente a las superficies de los cuerpos en contacto (conocidas como la dirección normal ) y las tensiones de fricción que actúan tangencialmente entre las superficies. Esta página se centra principalmente en la dirección normal, es decir, en la mecánica de contacto sin fricción. La mecánica de contacto por fricción se analiza por separado. Las tensiones normales son causadas por fuerzas aplicadas y por la adherencia presente en superficies en estrecho contacto, incluso si están limpias y secas.

La mecánica de contactos es parte de la ingeniería mecánica . La formulación física y matemática de la asignatura se basa en la mecánica de los materiales y la mecánica del continuo y se centra en cálculos que involucran cuerpos elásticos , viscoelásticos y plásticos en contacto estático o dinámico . La mecánica de contactos proporciona la información necesaria para el diseño seguro y energéticamente eficiente de sistemas técnicos y para el estudio de tribología , rigidez de contacto , resistencia de contacto eléctrico y dureza de indentación . Principios de la mecánica de contacto se implementan hacia aplicaciones tales como locomotora contacto rueda-carril, que acoplan los dispositivos, de frenado sistemas, neumáticos , rodamientos , motores de combustión , conexiones mecánicas , la junta sellos, trabajo de los metales , conformado de metales, soldadura ultrasónica , contactos eléctricos , y muchos otros. Los desafíos actuales que se enfrentan en el campo pueden incluir el análisis de tensión de los miembros de contacto y acoplamiento y la influencia de la lubricación y el diseño del material en la fricción y el desgaste . Las aplicaciones de la mecánica de contacto se extienden aún más al ámbito de la micro y la nanotecnología .

El trabajo original en mecánica de contacto se remonta a 1881 con la publicación del artículo "Sobre el contacto de sólidos elásticos" ( "Ueber die Berührung fester elastischer Körper" ) de Heinrich Hertz . Hertz estaba intentando comprender cómo las propiedades ópticas de múltiples lentes apiladas podrían cambiar con la fuerza que las mantenía juntas. La tensión de contacto hertziana se refiere a las tensiones localizadas que se desarrollan cuando dos superficies curvas entran en contacto y se deforman ligeramente bajo las cargas impuestas. Esta cantidad de deformación depende del módulo de elasticidad del material en contacto. Da la tensión de contacto en función de la fuerza de contacto normal, los radios de curvatura de ambos cuerpos y el módulo de elasticidad de ambos cuerpos. La tensión de contacto hertziana forma la base de las ecuaciones para la capacidad de carga y la vida útil a la fatiga en cojinetes, engranajes y cualquier otro cuerpo donde dos superficies estén en contacto.

Historia

La mecánica de contacto clásica se asocia más notablemente con Heinrich Hertz. En 1882, Hertz resolvió el problema de contacto de dos cuerpos elásticos con superficies curvas. Esta solución clásica todavía relevante proporciona una base para los problemas modernos en la mecánica de contactos. Por ejemplo, en ingeniería mecánica y tribología , la tensión de contacto hertziana es una descripción de la tensión dentro de las piezas acopladas. La tensión de contacto hertziana generalmente se refiere a la tensión cercana al área de contacto entre dos esferas de diferentes radios.

No fue hasta casi cien años después que Johnson , Kendall y Roberts encontraron una solución similar para el caso del contacto adhesivo . Esta teoría fue rechazada por Boris Derjaguin y sus colaboradores, quienes propusieron una teoría diferente de la adhesión en la década de 1970. El modelo Derjaguin llegó a ser conocido como modelo DMT (después de Derjaguin, Muller y Toporov), y Johnson et al. El modelo llegó a ser conocido como el modelo JKR (después de Johnson, Kendall y Roberts) para el contacto elástico adhesivo. Este rechazo resultó ser fundamental en el desarrollo de los parámetros Tabor y posteriores de Maugis que cuantifican qué modelo de contacto (de los modelos JKR y DMT) representan mejor el contacto adhesivo para materiales específicos.

Un mayor avance en el campo de la mecánica de contacto a mediados del siglo XX puede atribuirse a nombres como Bowden y Tabor . Bowden y Tabor fueron los primeros en enfatizar la importancia de la rugosidad superficial de los cuerpos en contacto. A través de la investigación de la rugosidad de la superficie, se encuentra que el área de contacto real entre los socios de fricción es menor que el área de contacto aparente. Esta comprensión también cambió drásticamente la dirección de las empresas en tribología. Los trabajos de Bowden y Tabor arrojaron varias teorías en la mecánica de contacto de superficies rugosas.

Las contribuciones de Archard (1957) también deben mencionarse en la discusión de trabajos pioneros en este campo. Archard concluyó que, incluso para superficies elásticas rugosas, el área de contacto es aproximadamente proporcional a la fuerza normal . Greenwood y Williamson (1966), Bush (1975) y Persson (2002) proporcionaron más información importante en este sentido. Los principales hallazgos de estos trabajos fueron que la verdadera superficie de contacto en materiales rugosos es generalmente proporcional a la fuerza normal, mientras que los parámetros de los microcontactos individuales (es decir, la presión, el tamaño del microcontacto) solo dependen débilmente de la carga. .

Soluciones clásicas para contacto elástico no adhesivo

La teoría del contacto entre cuerpos elásticos se puede utilizar para encontrar áreas de contacto y profundidades de indentación para geometrías simples. Algunas soluciones de uso común se enumeran a continuación. La teoría utilizada para calcular estas soluciones se analiza más adelante en este artículo. En

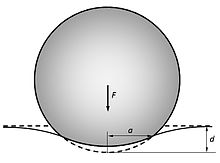
Contacto entre una esfera y un medio espacio.

Una esfera elástica de radio sangra un semiespacio elástico donde se encuentra la deformación total , lo que provoca un área de contacto de radio. ${\ Displaystyle R}$${\ Displaystyle d}$

${\ Displaystyle a = {\ sqrt {Rd}}}$

La fuerza aplicada está relacionada con el desplazamiento por ${\ Displaystyle F}$${\ Displaystyle d}$

${\ Displaystyle F = {\ frac {4} {3}} E ^ {*} R ^ {\ frac {1} {2}} d ^ {\ frac {3} {2}}}$

donde

${\ Displaystyle {\ frac {1} {E ^ {*}}} = {\ frac {1- \ nu _ {1} ^ {2}} {E_ {1}}} + {\ frac {1- \ nu _ {2} ^ {2}} {E_ {2}}}}$

y , son los módulos de elasticidad y , las relaciones de Poisson asociados a cada cuerpo. ${\ Displaystyle E_ {1}}$${\ Displaystyle E_ {2}}$${\ Displaystyle \ nu _ {1}}$${\ Displaystyle \ nu _ {2}}$

La distribución de la presión normal en el área de contacto en función de la distancia desde el centro del círculo es

${\ Displaystyle p (r) = p_ {0} \ left (1 - {\ frac {r ^ {2}} {a ^ {2}}} \ right) ^ {\ frac {1} {2}}}$

donde es la presión de contacto máxima dada por ${\ Displaystyle p_ {0}}$

${\ displaystyle p_ {0} = {\ frac {3F} {2 \ pi a ^ {2}}} = {\ frac {1} {\ pi}} \ left ({\ frac {6F {E ^ {* }} ^ {2}} {R ^ {2}}} \ right) ^ {\ frac {1} {3}}}$

El radio del círculo está relacionado con la carga aplicada por la ecuación ${\ Displaystyle F}$

${\ Displaystyle a ^ {3} = {\ cfrac {3FR} {4E ^ {*}}}}$

La deformación total está relacionada con la presión máxima de contacto por ${\ Displaystyle d}$

${\ Displaystyle d = {\ frac {a ^ {2}} {R}} = \ left ({\ frac {9F ^ {2}} {16 {E ^ {*}} ^ {2} R}} \ derecha) ^ {\ frac {1} {3}}}$

El esfuerzo cortante máximo se produce en el interior en para . ${\ Displaystyle z \ approx 0.49a}$${\ Displaystyle \ nu = 0.33}$

Contacto entre dos esferas

Para el contacto entre dos esferas de radio y , el área de contacto es un círculo de radio . Las ecuaciones son las mismas que para una esfera en contacto con un semiplano excepto que el radio efectivo se define como ${\ Displaystyle R_ {1}}$${\ Displaystyle R_ {2}}$${\ Displaystyle a}$${\ Displaystyle R}$

${\ Displaystyle {\ frac {1} {R}} = {\ frac {1} {R_ {1}}} + {\ frac {1} {R_ {2}}}}$

Contacto entre dos cilindros cruzados de igual radio ${\ Displaystyle R}$

Esto es equivalente al contacto entre una esfera de radio y un plano . ${\ Displaystyle R}$

Contacto entre un cilindro rígido con extremo plano y un semiespacio elástico

Si un cilindro rígido se presiona en un semiespacio elástico, crea una distribución de presión descrita por

${\ Displaystyle p (r) = p_ {0} \ left (1 - {\ frac {r ^ {2}} {R ^ {2}}} \ right) ^ {- {\ frac {1} {2} }}}$

donde es el radio del cilindro y ${\ Displaystyle R}$

${\ displaystyle p_ {0} = {\ frac {1} {\ pi}} E ^ {*} {\ frac {d} {R}}}$

La relación entre la profundidad de la hendidura y la fuerza normal viene dada por

${\ displaystyle F = 2RE ^ {*} d}$

Contacto entre un penetrador cónico rígido y un semiespacio elástico

En el caso de la indentación de un semiespacio elástico del módulo de Young utilizando un indentador cónico rígido , la profundidad de la región de contacto y el radio de contacto están relacionados por ${\ Displaystyle E}$${\ Displaystyle \ epsilon}$${\ Displaystyle a}$

${\ Displaystyle \ epsilon = a \ tan (\ theta)}$

con definido como el ángulo entre el plano y la superficie lateral del cono. La profundidad total de la sangría viene dada por: ${\ Displaystyle \ theta}$${\ Displaystyle d}$

${\ Displaystyle d = {\ frac {\ pi} {2}} \ epsilon}$

La fuerza total es

${\ Displaystyle F = {\ frac {\ pi E} {2 \ left (1- \ nu ^ {2} \ right)}} a ^ {2} \ tan (\ theta) = {\ frac {2E} { \ pi \ left (1- \ nu ^ {2} \ right)}} {\ frac {d ^ {2}} {\ tan (\ theta)}}}$

La distribución de la presión está dada por

${\ Displaystyle p \ left (r \ right) = {\ frac {Ed} {\ pi a \ left (1- \ nu ^ {2} \ right)}} \ ln \ left ({\ frac {a} { r}} + {\ sqrt {\ left ({\ frac {a} {r}} \ right) ^ {2} -1}} \ right) = {\ frac {Ed} {\ pi a \ left (1 - \ nu ^ {2} \ right)}} \ cosh ^ {- 1} \ left ({\ frac {a} {r}} \ right)}$

La tensión tiene una singularidad logarítmica en la punta del cono.

Contacto entre dos cilindros con ejes paralelos

En contacto entre dos cilindros con ejes paralelos, la fuerza es linealmente proporcional a la longitud de los cilindros L y a la profundidad de indentación d :

${\ Displaystyle F \ approx {\ frac {\ pi} {4}} E ^ {*} Ld}$

Los radios de curvatura están completamente ausentes de esta relación. El radio de contacto se describe mediante la relación habitual

${\ Displaystyle a = {\ sqrt {Rd}}}$

con

${\ Displaystyle {\ frac {1} {R}} = {\ frac {1} {R_ {1}}} + {\ frac {1} {R_ {2}}}}$

como en contacto entre dos esferas. La presión máxima es igual a

${\ displaystyle p_ {0} = \ left ({\ frac {E ^ {*} F} {\ pi LR}} \ right) ^ {\ frac {1} {2}}}$

Contacto de rodamientos

El contacto en el caso de los rodamientos es a menudo un contacto entre una superficie convexa (cilindro macho o esfera) y una superficie cóncava (cilindro hembra o esfera: agujero o copa hemisférica ).

El método de reducción de dimensionalidad

Algunos problemas de contacto se pueden resolver con el método de reducción de dimensionalidad (MDR). En este método, el sistema tridimensional inicial se reemplaza con un contacto de un cuerpo con una base elástica lineal o viscoelástica (ver fig.). Las propiedades de los sistemas unidimensionales coinciden exactamente con las del sistema tridimensional original, si se modifica la forma de los cuerpos y se definen los elementos de la cimentación según las reglas del MDR. MDR se basa en la solución a problemas de contacto axisimétrico obtenida por primera vez por Ludwig Föppl (1941) y Gerhard Schubert (1942)

Sin embargo, para obtener resultados analíticos exactos, se requiere que el problema del contacto sea simétrico y que los contactos sean compactos.

Teoría hertziana del contacto elástico no adhesivo

La teoría clásica del contacto se centró principalmente en el contacto no adhesivo donde no se permite que ocurra ninguna fuerza de tensión dentro del área de contacto, es decir, los cuerpos en contacto pueden separarse sin fuerzas de adhesión. Se han utilizado varios enfoques analíticos y numéricos para resolver problemas de contacto que satisfacen la condición de no adherencia. Se transmiten fuerzas y momentos complejos entre los cuerpos donde se tocan, por lo que los problemas en la mecánica de contacto pueden volverse bastante sofisticados. Además, las tensiones de contacto suelen ser una función no lineal de la deformación. Para simplificar el procedimiento de solución, generalmente se define un marco de referencia en el que los objetos (posiblemente en movimiento entre sí) son estáticos. Interactúan a través de tracciones superficiales (o presiones / tensiones) en su interfaz.

Como ejemplo, considere dos objetos que se encuentran en alguna superficie en el plano ( , ) con el eje-asumido normal a la superficie. Uno de los cuerpos experimentará una distribución de presión normalmente dirigida y distribuciones de tracción de superficie en el plano y sobre la región . En términos de un equilibrio de fuerzas newtoniano , las fuerzas: ${\ Displaystyle S}$${\ Displaystyle x}$${\ Displaystyle y}$${\ Displaystyle z}$${\ Displaystyle p_ {z} = p (x, y) = q_ {z} (x, y)}$${\ Displaystyle q_ {x} = q_ {x} (x, y)}$${\ Displaystyle q_ {y} = q_ {y} (x, y)}$${\ Displaystyle S}$

${\ Displaystyle P_ {z} = \ int _ {S} p (x, y) ~ \ mathrm {d} A ~; ~~ Q_ {x} = \ int _ {S} q_ {x} (x, y ) ~ \ mathrm {d} A ~; ~~ Q_ {y} = \ int _ {S} q_ {y} (x, y) ~ \ mathrm {d} A}$

debe ser igual y opuesto a las fuerzas establecidas en el otro cuerpo. Los momentos correspondientes a estas fuerzas:

${\ Displaystyle M_ {x} = \ int _ {S} y ~ q_ {z} (x, y) ~ \ mathrm {d} A ~; ~~ M_ {y} = \ int _ {S} -x ~ q_ {z} (x, y) ~ \ mathrm {d} A ~; ~~ M_ {z} = \ int _ {S} [x ~ q_ {y} (x, y) -y ~ q_ {x} (x, y)] ~ \ mathrm {d} A}$

También se requiere que se cancelen entre cuerpos para que estén cinemáticamente inmóviles.

Supuestos en la teoría hertziana

Se realizan las siguientes suposiciones para determinar las soluciones de los problemas de contacto hertzianos :

• Las deformaciones son pequeñas y están dentro del límite elástico.
• Las superficies son continuas y no conformes (lo que implica que el área de contacto es mucho más pequeña que las dimensiones características de los cuerpos en contacto).
• Cada cuerpo puede considerarse un semiespacio elástico.
• Las superficies no tienen fricción.

Surgen complicaciones adicionales cuando se violan algunas o todas estas suposiciones y tales problemas de contacto generalmente se denominan no hertzianos .

Técnicas de solución analítica

Los métodos de solución analítica para problemas de contacto no adhesivo se pueden clasificar en dos tipos según la geometría del área de contacto. Un contacto conforme es aquel en el que los dos cuerpos se tocan en múltiples puntos antes de que se produzca cualquier deformación (es decir, simplemente "encajan"). Un contacto no conforme es aquel en el que las formas de los cuerpos son lo suficientemente diferentes como para que, bajo carga cero, solo se toquen en un punto (o posiblemente a lo largo de una línea). En el caso de disconformidad, el área de contacto es pequeña en comparación con los tamaños de los objetos y las tensiones están muy concentradas en esta área. Tal contacto se llama concentrado , de lo contrario se llama diversificado .

Un enfoque común en la elasticidad lineal es superponer una serie de soluciones, cada una de las cuales corresponde a una carga puntual que actúa sobre el área de contacto. Por ejemplo, en el caso de la carga de un semiplano , la solución Flamant se utiliza a menudo como punto de partida y luego se generaliza a varias formas del área de contacto. Los equilibrios de fuerza y ​​momento entre los dos cuerpos en contacto actúan como restricciones adicionales a la solución.

Punto de contacto en un semiplano (2D)

Un punto de partida para resolver problemas de contacto es comprender el efecto de una "carga puntual" aplicada a un semiplano elástico isotrópico, homogéneo y lineal, que se muestra en la figura de la derecha. El problema puede ser una tensión plana o una tensión plana . Este es un problema de valor límite de elasticidad lineal sujeto a las condiciones límite de tracción :

${\ Displaystyle \ sigma _ {xz} (x, 0) = 0 ~; ~~ \ sigma _ {z} (x, z) = - P \ delta (x, z)}$

donde está la función delta de Dirac . Las condiciones de contorno establecen que no hay esfuerzos cortantes en la superficie y se aplica una fuerza normal P singular en (0, 0). La aplicación de estas condiciones a las ecuaciones de elasticidad que gobiernan produce el resultado ${\ Displaystyle \ delta (x, z)}$

${\ Displaystyle {\ begin {alineado} \ sigma _ {xx} & = - {\ frac {2P} {\ pi}} {\ frac {x ^ {2} z} {\ left (x ^ {2} + z ^ {2} \ right) ^ {2}}} \\\ sigma _ {zz} & = - {\ frac {2P} {\ pi}} {\ frac {z ^ {3}} {\ left ( x ^ {2} + z ^ {2} \ right) ^ {2}}} \\\ sigma _ {xz} & = - {\ frac {2P} {\ pi}} {\ frac {xz ^ {2 }} {\ left (x ^ {2} + z ^ {2} \ right) ^ {2}}} \ end {alineado}}}$

en algún momento, en el semiplano. El círculo que se muestra en la figura indica una superficie en la que el esfuerzo cortante máximo es constante. A partir de este campo de tensión, se pueden determinar los componentes de deformación y, por tanto, los desplazamientos de todos los puntos del material. ${\ Displaystyle (x, y)}$

Contacto de línea en un semiplano (2D)

Carga normal sobre una región ${\ Displaystyle (a, b)}$

Suponga que, en lugar de una carga puntual , se aplica una carga distribuida a la superficie, sobre el rango . El principio de superposición lineal se puede aplicar para determinar el campo de tensión resultante como solución a las ecuaciones integrales : ${\ Displaystyle P}$${\ Displaystyle p (x)}$${\ Displaystyle a <x <b}$

${\ Displaystyle {\ begin {alineado} \ sigma _ {xx} & = - {\ frac {2z} {\ pi}} \ int _ {a} ^ {b} {\ frac {p \ left (x '\ derecha) \ left (x-x '\ right) ^ {2} \, dx'} {\ left [\ left (x-x '\ right) ^ {2} + z ^ {2} \ right] ^ { 2}}} ~; ~~ \ sigma _ {zz} = - {\ frac {2z ^ {3}} {\ pi}} \ int _ {a} ^ {b} {\ frac {p \ left (x '\ right) \, dx'} {\ left [\ left (x-x '\ right) ^ {2} + z ^ {2} \ right] ^ {2}}} \\ [3pt] \ sigma _ {xz} & = - {\ frac {2z ^ {2}} {\ pi}} \ int _ {a} ^ {b} {\ frac {p \ left (x '\ right) \ left (x-x '\ right) \, dx'} {\ left [\ left (x-x '\ right) ^ {2} + z ^ {2} \ right] ^ {2}}} \ end {alineado}}}$

Carga de cizallamiento sobre una región ${\ Displaystyle (a, b)}$

El mismo principio se aplica para la carga en la superficie en el plano de la superficie. Este tipo de tracciones tienden a surgir como resultado de la fricción. La solución es similar a la anterior (tanto para cargas singulares como distribuidas ) pero ligeramente modificada: ${\ displaystyle Q}$${\ Displaystyle q (x)}$

${\ Displaystyle {\ begin {alineado} \ sigma _ {xx} & = - {\ frac {2} {\ pi}} \ int _ {a} ^ {b} {\ frac {q \ left (x '\ derecha) \ left (x-x '\ right) ^ {3} \, dx'} {\ left [\ left (x-x '\ right) ^ {2} + z ^ {2} \ right] ^ { 2}}} ~; ~~ \ sigma _ {zz} = - {\ frac {2z ^ {2}} {\ pi}} \ int _ {a} ^ {b} {\ frac {q \ left (x '\ right) \ left (x-x' \ right) \, dx '} {\ left [\ left (x-x' \ right) ^ {2} + z ^ {2} \ right] ^ {2} }} \\ [3pt] \ sigma _ {xz} & = - {\ frac {2z} {\ pi}} \ int _ {a} ^ {b} {\ frac {q \ left (x '\ right) \ left (x-x '\ right) ^ {2} \, dx'} {\ left [\ left (x-x '\ right) ^ {2} + z ^ {2} \ right] ^ {2} }} \ end {alineado}}}$

Estos resultados pueden superponerse a los dados anteriormente para cargas normales para hacer frente a cargas más complejas.

Punto de contacto en un medio espacio (3D)

De manera análoga a la solución Flamant para el semiplano 2D, también se conocen soluciones fundamentales para el semiespacio 3D linealmente elástico. Estos fueron encontrados por Boussinesq para una carga normal concentrada y por Cerruti para una carga tangencial. Consulte la sección sobre esto en Elasticidad lineal .

Técnicas de solución numérica

No es necesario hacer distinciones entre contacto conforme y no conforme cuando se emplean esquemas de solución numérica para resolver problemas de contacto. Estos métodos no se basan en supuestos adicionales dentro del proceso de solución, ya que se basan únicamente en la formulación general de las ecuaciones subyacentes. Además de las ecuaciones estándar que describen la deformación y el movimiento de los cuerpos, se pueden formular dos desigualdades adicionales. El primero simplemente restringe el movimiento y la deformación de los cuerpos asumiendo que no puede ocurrir ninguna penetración. Por lo tanto, la brecha entre dos cuerpos solo puede ser positiva o cero. ${\ Displaystyle h}$

${\ Displaystyle h \ geq 0}$

donde denota contacto. La segunda suposición en la mecánica de contacto está relacionada con el hecho de que no se permite que se produzca fuerza de tensión dentro del área de contacto (los cuerpos en contacto se pueden levantar sin fuerzas de adhesión). Esto conduce a una desigualdad que las tensiones deben obedecer en la interfaz de contacto. Está formulado para el estrés normal . ${\ Displaystyle h = 0}$${\ Displaystyle \ sigma _ {n} = \ mathbf {t} \ cdot \ mathbf {n}}$

En los lugares donde hay contacto entre las superficies de la brecha es cero, es decir , y no la tensión normal es diferente de cero, en efecto, . En lugares donde las superficies no están en contacto, la tensión normal es idéntica a cero; , mientras que la brecha es positiva; es decir, . Este tipo de formulación de complementariedad se puede expresar en la denominada forma de Kuhn-Tucker , a saber. ${\ Displaystyle h = 0}$${\ Displaystyle \ sigma _ {n} <0}$${\ Displaystyle \ sigma _ {n} = 0}$${\ Displaystyle h> 0}$

${\ Displaystyle h \ geq 0 \ ,, \ quad \ sigma _ {n} \ leq 0 \ ,, \ quad \ sigma _ {n} \, h = 0 \ ,.}$

Estas condiciones son válidas de forma general. La formulación matemática del espacio depende de la cinemática de la teoría subyacente del sólido (por ejemplo, sólido lineal o no lineal en dos o tres dimensiones, modelo de viga o capa ). Reafirmando la tensión normal en términos de la presión de contacto ,; es decir, el problema de Kuhn-Tucker puede reformularse como en la forma estándar de complementariedad, es decir,${\ Displaystyle \ sigma _ {n}}$${\ Displaystyle p}$${\ Displaystyle p = - \ sigma _ {n}}$

En el caso elástico lineal, el espacio se puede formular como donde es la separación del cuerpo rígido, es la geometría / topografía del contacto (cilindro y rugosidad) y es la deformación / deflexión elástica. Si los cuerpos en contacto se aproximan como semiespacios elásticos lineales, se puede aplicar la solución de la ecuación integral de Boussinesq-Cerruti para expresar la deformación ( ) en función de la presión de contacto ( ); es decir,${\ Displaystyle h_ {0}}$${\ Displaystyle g}$${\ Displaystyle u}$${\ Displaystyle u}$${\ Displaystyle p}$ donde para la carga lineal de un medio espacio elástico y para la carga puntual de un semiespacio elástico.

Después de la discretización, el problema de la mecánica de contacto elástico lineal se puede plantear en la forma estándar de problema de complementariedad lineal (LCP).

${\ Displaystyle {\ begin {alineado} \ mathbf {h} & ​​= \ mathbf {h} _ {0} + \ mathbf {g} + \ mathbf {Cp}, \\\ mathbf {h} \ cdot \ mathbf { p} & = 0, \, \, \, \ mathbf {p} \ geq 0, \, \, \, \ mathbf {h} \ geq 0, \\\ end {alineado}}}$

donde es una matriz, cuyos elementos se denominan coeficientes de influencia que relacionan la presión de contacto y la deformación. La estricta formulación LCP del problema CM presentado anteriormente permite la aplicación directa de técnicas de solución numérica bien establecidas, como el algoritmo de pivote de Lemke . El algoritmo de Lemke tiene la ventaja de que encuentra la solución numéricamente exacta dentro de un número finito de iteraciones. La implementación de MATLAB presentada por Almqvist et al. es un ejemplo que se puede emplear para resolver el problema numéricamente. Además, un código de ejemplo para una solución LCP de un problema de mecánica de contacto elástico lineal 2D también se ha hecho público en el intercambio de archivos MATLAB por Almqvist et al.${\ Displaystyle \ mathbf {C}}$

Contacto entre superficies rugosas

Cuando dos cuerpos con superficies rugosas se presionan entre sí, el área de contacto real que se forma entre los dos cuerpos es mucho más pequeña que el área de contacto aparente o nominal . La mecánica del contacto con superficies rugosas se discute en términos de la mecánica de contacto normal y las interacciones de fricción estática. Las superficies naturales y de ingeniería típicamente exhiben características de rugosidad, conocidas como asperezas, en una amplia gama de escalas de longitud hasta el nivel molecular, con estructuras de superficie que exhiben autoafinidad, también conocida como fractalidad de superficie . Se reconoce que la estructura auto afín de las superficies es el origen de la escala lineal del área de contacto real con la presión aplicada. Suponiendo un modelo de contactos soldados por cizallamiento en interacciones tribológicas , esta linealidad observada ubicuamente entre el área de contacto y la presión también puede considerarse el origen de la linealidad de la relación entre la fricción estática y la fuerza normal aplicada. ${\ Displaystyle A}$${\ Displaystyle A_ {0}}$

En contacto entre una superficie "rugosa aleatoria" y un semiespacio elástico, el área de contacto real está relacionada con la fuerza normal por ${\ Displaystyle F}$

${\ Displaystyle A = {\ frac {\ kappa} {E ^ {*} h '}} F}$

con igual a la raíz cuadrada media (también conocida como la media cuadrática) de la pendiente de la superficie y . La presión media en la verdadera superficie de contacto. ${\ Displaystyle h '}$${\ Displaystyle \ kappa \ approx 2}$

${\ Displaystyle p _ {\ mathrm {av}} = {\ frac {F} {A}} \ approx {\ frac {1} {2}} E ^ {*} h '}$

se puede estimar razonablemente como la mitad del módulo elástico efectivo multiplicado por la raíz cuadrada media de la pendiente de la superficie . ${\ Displaystyle E ^ {*}}$${\ Displaystyle h '}$

Una descripción general del modelo GW

Greenwood y Williamson en 1966 (GW) propusieron una teoría de la mecánica de contacto elástico de superficies rugosas que es hoy la base de muchas teorías en tribología (fricción, adhesión, conductancia térmica y eléctrica, desgaste, etc.). Consideraron el contacto entre un plano rígido liso y una superficie rugosa deformable nominalmente plana cubierta con asperezas de punta redonda del mismo radio R. Su teoría asume que la deformación de cada aspereza es independiente de la de sus vecinas y está descrita por el modelo de Hertz . Las alturas de las asperezas tienen una distribución aleatoria. La probabilidad de que la altura de la aspereza esté entre y es . Los autores calcularon el número de puntos de contacto n, el área de contacto total y la carga total P en el caso general. Dieron esas fórmulas en dos formas: en la básica y usando variables estandarizadas. Si se supone que N asperezas cubren una superficie rugosa, entonces el número esperado de contactos es ${\ Displaystyle z}$${\ Displaystyle z + dz}$${\ Displaystyle \ phi (z) dz}$${\ Displaystyle A_ {r}}$

${\ Displaystyle n = N \ int _ {d} ^ {\ infty} \ phi (z) dz}$

El área de contacto total esperada se puede calcular a partir de la fórmula

${\ Displaystyle A_ {a} = N \ pi R \ int _ {d} ^ {\ infty} (zd) \ phi (z) dz}$

y la fuerza total esperada viene dada por

${\ Displaystyle P = {\ frac {4} {3}} NE_ {r} {\ sqrt {R}} \ int _ {d} ^ {\ infty} (zd) ^ {\ frac {3} {2} } \ phi (z) dz}$

donde:

R, radio de curvatura de la microasperidad,

z, altura de la microasperidad medida desde la línea del perfil,

d, cierra la superficie,

${\ Displaystyle E_ {r} = \ left ({\ frac {1- \ nu _ {1} ^ {2}} {E_ {1}}} + {\ frac {1- \ nu _ {2} ^ { 2}} {E_ {2}}} \ right) ^ {- 1}}$, módulo de elasticidad de Young compuesto,

${\ Displaystyle E_ {i}}$, módulo de elasticidad de la superficie,

${\ Displaystyle \ nu _ {i}}$, Coeficientes de superficie de Poisson.

Introdujeron la separación estandarizada y la distribución de altura estandarizada cuya desviación estándar es igual a uno. A continuación se presentan las fórmulas en forma estandarizada. ${\ Displaystyle h = d / \ sigma}$${\ Displaystyle \ phi ^ {*} (s)}$

${\ Displaystyle {\ begin {alineado} F_ {n} (h) & = \ int _ {h} ^ {\ infty} (sh) ^ {n} \ phi ^ {*} (s) ds \\ n & = \ eta A_ {n} F_ {0} (h) \\ A_ {a} & = \ pi \ eta AR \ sigma F_ {1} (h) \\ P & = {\ frac {4} {3}} \ eta AE_ {r} {\ sqrt {R}} \ sigma ^ {\ frac {3} {2}} F _ {\ frac {3} {2}} (h) \ end {alineado}}}$

donde:

d es la separación,

${\ Displaystyle A}$ es el área de contacto nominal,

${\ Displaystyle \ eta}$ es la densidad superficial de las asperezas,

${\ Displaystyle E ^ {*}}$ es el módulo de Young efectivo.

Recientemente, las aproximaciones exactas y fueron publicadas por Jedynak. Están dadas por las siguientes fórmulas racionales, que son aproximaciones muy exactas de integrales . Se calculan para la distribución gaussiana de asperezas. ${\ Displaystyle A_ {r}}$${\ Displaystyle P}$${\ Displaystyle F_ {n} (h)}$

${\ Displaystyle F_ {n} (h) = {\ frac {a_ {0} + a_ {1} h + a_ {2} h ^ {2} + a_ {3} h ^ {3}} {1 + b_ {1} h + b_ {2} h ^ {2} + b_ {3} h ^ {3} + b_ {4} h ^ {4} + b_ {5} h ^ {5} + b_ {6} h ^ {6}}} \ exp \ left (- {\ frac {h ^ {2}} {2}} \ right)}$

Porque los coeficientes son ${\ Displaystyle F_ {1} (h)}$

${\ displaystyle {\ begin {alineado} [] [a_ {0}, a_ {1}, a_ {2}, a_ {3}] & = [0.398942280401,0.159773702775,0.0389687688311,0.00364356495452] \\ [] [b_ { 1}, b_ {2}, b_ {3}, b_ {4}, b_ {5}, b_ {6}] & = \ left [1.653807476138,1.170419428529,0.448892964428,0.0951971709160,0.00931642803836, -6.383774657279 \ times 10 ^ { -6} \ right] \ end {alineado}}}$

El error relativo máximo es . ${\ Displaystyle 9,93 \ times 10 ^ {- 8} \%}$

Porque los coeficientes son ${\ Displaystyle F _ {\ frac {3} {2}} (h)}$

${\ displaystyle {\ begin {alineado} [] [a_ {0}, a_ {1}, a_ {2}, a_ {3}] & = [0.430019993662,0.101979509447,0.0229040629580,0.000688602924] \\ [] [b_ { 1}, b_ {2}, b_ {3}, b_ {4}, b_ {5}, b_ {6}] & = [1.671117125984,1.199586555505,0.46936532151,0.102632881122,0.010686348714,0.0000517200271] \ end {alineado}}}$

El error relativo máximo es . El documento también contiene las expresiones exactas para${\ Displaystyle 1,91 \ times 10 ^ {- 7} \%}$${\ Displaystyle F_ {n} (h)}$

${\ Displaystyle {\ begin {alineado} F_ {1} (h) & = {\ frac {1} {\ sqrt {2 \ pi}}} \ exp \ left (- {\ frac {1} {2}} h ^ {2} \ right) - {\ frac {1} {2}} h \, \ operatorname {erfc} \ left ({\ frac {h} {\ sqrt {2}}} \ right) \\ F_ {\ frac {3} {2}} (h) & = {\ frac {1} {4 {\ sqrt {\ pi}}}} \ exp \ left (- {\ frac {h ^ {2}} { 4}} \ right) {\ sqrt {h}} \ left (\ left (h ^ {2} +1 \ right) K _ {\ frac {1} {4}} \ left ({\ frac {h ^ { 2}} {4}} \ derecha) -h ^ {2} K _ {\ frac {3} {4}} \ izquierda ({\ frac {h ^ {2}} {4}} \ derecha) \ derecha) \ end {alineado}}}$

donde erfc (z) significa la función de error complementaria y es la función de Bessel modificada del segundo tipo. ${\ Displaystyle K _ {\ nu} (z)}$

Para la situación en la que las asperezas en las dos superficies tienen una distribución de altura gaussiana y se puede suponer que los picos son esféricos, la presión de contacto promedio es suficiente para producir fluencia cuando dónde está el límite elástico uniaxial y la dureza de indentación. Greenwood y Williamson definieron un parámetro adimensional llamado índice de plasticidad que podría usarse para determinar si el contacto sería elástico o plástico. ${\ Displaystyle p _ {\ text {av}} = 1,1 \ sigma _ {y} \ aproximadamente 0,39 \ sigma _ {0}}$${\ Displaystyle \ sigma _ {y}}$${\ Displaystyle \ sigma _ {0}}$${\ Displaystyle \ Psi}$

El modelo de Greenwood-Williamson requiere el conocimiento de dos cantidades estadísticamente dependientes; la desviación estándar de la rugosidad de la superficie y la curvatura de los picos de aspereza. Mikic ha dado una definición alternativa del índice de plasticidad. El rendimiento se produce cuando la presión es mayor que el límite elástico uniaxial. Dado que el límite elástico es proporcional a la dureza de la indentación , Mikic definió el índice de plasticidad para el contacto elástico-plástico como ${\ Displaystyle \ sigma _ {0}}$

${\ Displaystyle \ Psi = {\ frac {E ^ {*} h '} {\ sigma _ {0}}}> {\ frac {2} {3}} ~.}$

En esta definición, representa la microrrugosidad en un estado de plasticidad completa y solo se necesita una cantidad estadística, la pendiente rms, que se puede calcular a partir de mediciones de superficie. Porque , la superficie se comporta elásticamente durante el contacto. ${\ Displaystyle \ Psi}$${\ Displaystyle \ Psi <{\ frac {2} {3}}}$

En los modelos de Greenwood-Williamson y Mikic, se supone que la carga es proporcional al área deformada. Por tanto, si el sistema se comporta plástica o elásticamente es independiente de la fuerza normal aplicada.

Una descripción general del modelo GT

El modelo propuesto por Greenwood y Tripp (GT), extendió el modelo GW al contacto entre dos superficies rugosas. El modelo GT se utiliza ampliamente en el campo del análisis elastohidrodinámico.

Las ecuaciones citadas con más frecuencia dadas por el modelo GT son para el área de contacto de aspereza

${\ Displaystyle A_ {a} = \ pi ^ {2} (\ eta \ beta \ sigma) ^ {2} AF_ {2} (\ lambda),}$

y carga llevada por asperezas

${\ Displaystyle P = {\ frac {8 {\ sqrt {2}}} {15}} \ pi (\ eta \ beta \ sigma) ^ {2} {\ sqrt {\ frac {\ sigma} {\ beta} }} E'AF _ {\ frac {5} {2}} (\ lambda),}$

donde:

${\ Displaystyle \ eta \ beta \ sigma}$, parámetro de rugosidad,

${\ Displaystyle A}$, área de contacto nominal,

${\ Displaystyle \ lambda}$, Parámetro de película de aceite de Stribeck, definido por primera vez por Stribeck \ cite {gt} como ,${\ Displaystyle \ lambda = h / \ sigma}$

${\ Displaystyle E '}$, módulo de elasticidad efectivo,

${\ Displaystyle F_ {2}, F _ {\ frac {5} {2}} (\ lambda)}$, funciones estadísticas introducidas para coincidir con la distribución gaussiana de asperezas asumida.

Las soluciones exactas para y son presentadas en primer lugar por Jedynak. Se expresan de la siguiente manera ${\ Displaystyle A_ {a}}$${\ Displaystyle P}$${\ Displaystyle F_ {n}}$

${\ displaystyle {\ begin {alineado} F_ {2} & = {\ frac {1} {2}} \ left (h ^ {2} +1 \ right) \ operatorname {erfc} \ left ({\ frac { h} {\ sqrt {2}}} \ right) - {\ frac {h} {\ sqrt {2 \ pi}}} \ exp \ left (- {\ frac {h ^ {2}} {2}} \ right) \\ F _ {\ frac {5} {2}} & = {\ frac {1} {8 {\ sqrt {\ pi}}}} \ exp \ left (- {\ frac {h ^ {2 }} {4}} \ right) h ^ {\ frac {3} {2}} \ left (\ left (2h ^ {2} +3 \ right) K _ {\ frac {3} {4}} \ left ({\ frac {h ^ {2}} {4}} \ right) - \ left (2h ^ {2} +5 \ right) K _ {\ frac {1} {4}} \ left ({\ frac { h ^ {2}} {4}} \ right) \ right) \ end {alineado}}}$

donde erfc (z) significa la función de error complementaria y es la función de Bessel modificada del segundo tipo. ${\ Displaystyle K _ {\ nu} (z)}$

En el papel se puede encontrar una revisión exhaustiva de las aproximaciones existentes a . Las nuevas propuestas dan las aproximaciones más precisas de y , que se informan en la literatura. Están dadas por las siguientes fórmulas racionales, que son aproximaciones muy exactas de integrales . Se calculan para la distribución gaussiana de asperezas. ${\ Displaystyle F _ {\ frac {5} {2}}}$${\ Displaystyle F _ {\ frac {5} {2}}}$${\ Displaystyle F_ {2}}$${\ Displaystyle F_ {n} (h)}$

${\ Displaystyle F_ {n} (h) = {\ frac {a_ {0} + a_ {1} h + a_ {2} h ^ {2} + a_ {3} h ^ {3}} {1 + b_ {1} h + b_ {2} h ^ {2} + b_ {3} h ^ {3} + b_ {4} h ^ {4} + b_ {5} h ^ {5} + b_ {6} h ^ {6}}} \ exp \ left (- {\ frac {h ^ {2}} {2}} \ right)}$

Porque los coeficientes son ${\ Displaystyle F_ {2} (h)}$

${\ displaystyle {\ begin {alineado} [] [a_ {0}, a_ {1}, a_ {2}, a_ {3}] & = [0.5,0.182536384941,0.039812283118,0.003684879001] \\ [] [b_ { 1}, b_ {2}, b_ {3}, b_ {4}, b_ {5}, b_ {6}] & = [1.960841785003,1.708677456715,0.856592986083,0.264996791567,0.049257843893,0.004640740133] \ end {alineado}}}$

El error relativo máximo es . ${\ Displaystyle 1,68 \ times 10 ^ {- 7} \%}$

Porque los coeficientes son ${\ Displaystyle F _ {\ frac {5} {2}} (h)}$

${\ displaystyle {\ begin {alineado} [] [a_ {0}, a_ {1}, a_ {2}, a_ {3}] & = [0.616634218997,0.108855827811,0.023453835635,0.000449332509] \\ [] [b_ { 1}, b_ {2}, b_ {3}, b_ {4}, b_ {5}, b_ {6}] & = [1.919948267476,1.635304362591,0.799392556572,0.240278859212,0.043178653945,0.003863334276] \ end {alineado}}}$

El error relativo máximo es . ${\ Displaystyle 4.98 \ times 10 ^ {- 8} \%}$

Contacto adhesivo entre cuerpos elásticos

Cuando dos superficies sólidas se acercan, experimentan atractivas fuerzas de van der Waals . El modelo de van der Waals de Bradley proporciona un medio para calcular la fuerza de tracción entre dos esferas rígidas con superficies perfectamente lisas. El modelo de contacto hertziano no considera posible la adhesión. Sin embargo, a fines de la década de 1960, se observaron varias contradicciones cuando se comparó la teoría de Hertz con experimentos que involucraban el contacto entre esferas de caucho y vidrio.

Se observó que, aunque la teoría de Hertz se aplicaba a grandes cargas, a bajas cargas

• el área de contacto era mayor que la predicha por la teoría de Hertz,
• el área de contacto tenía un valor distinto de cero incluso cuando se quitó la carga, y
• incluso hubo una fuerte adherencia si las superficies de contacto estaban limpias y secas.

Esto indicó que las fuerzas adhesivas estaban en acción. El modelo Johnson-Kendall-Roberts (JKR) y los modelos Derjaguin-Muller-Toporov (DMT) fueron los primeros en incorporar la adhesión en el contacto hertziano.

Modelo Bradley de contacto rígido

Se asume comúnmente que la fuerza superficial entre dos planos atómicos a una distancia entre sí puede derivarse del potencial de Lennard-Jones . Con esta suposición ${\ Displaystyle z}$

${\ displaystyle F (z) = {\ cfrac {16 \ gamma} {3z_ {0}}} \ left [\ left ({\ cfrac {z} {z_ {0}}} \ right) ^ {- 9} - \ left ({\ cfrac {z} {z_ {0}}} \ right) ^ {- 3} \ right]}$

donde es la fuerza (positiva en compresión), es la energía superficial total de ambas superficies por unidad de área y es la separación de equilibrio de los dos planos atómicos. ${\ Displaystyle F}$${\ Displaystyle 2 \ gamma}$${\ Displaystyle z_ {0}}$

El modelo de Bradley aplicó el potencial de Lennard-Jones para encontrar la fuerza de adhesión entre dos esferas rígidas. Se encuentra que la fuerza total entre las esferas es

${\ Displaystyle F_ {a} (z) = {\ cfrac {16 \ gamma \ pi R} {3}} \ left [{\ cfrac {1} {4}} \ left ({\ cfrac {z} {z_ {0}}} \ right) ^ {- 8} - \ left ({\ cfrac {z} {z_ {0}}} \ right) ^ {- 2} \ right] ~; ~~ {\ frac {1 } {R}} = {\ frac {1} {R_ {1}}} + {\ frac {1} {R_ {2}}}}$

donde están los radios de las dos esferas. ${\ Displaystyle R_ {1}, R_ {2}}$

Las dos esferas se separan completamente cuando se logra la fuerza de extracción, en cuyo punto ${\ Displaystyle z = z_ {0}}$

${\ Displaystyle F_ {a} = F_ {c} = - 4 \ gamma \ pi R.}$

Modelo de contacto elástico de Johnson-Kendall-Roberts (JKR)

Para incorporar el efecto de la adhesión en el contacto hertziano, Johnson, Kendall y Roberts formularon la teoría JKR del contacto adhesivo utilizando un equilibrio entre la energía elástica almacenada y la pérdida de energía superficial . El modelo JKR considera el efecto de la presión de contacto y la adhesión solo dentro del área de contacto. La solución general para la distribución de presión en el área de contacto en el modelo JKR es

${\ Displaystyle p (r) = p_ {0} \ left (1 - {\ frac {r ^ {2}} {a ^ {2}}} \ right) ^ {\ frac {1} {2}} + p_ {0} '\ left (1 - {\ frac {r ^ {2}} {a ^ {2}}} \ right) ^ {- {\ frac {1} {2}}}}$

Tenga en cuenta que en la teoría de Hertz original, el término contención se descuidó porque la tensión no podía sostenerse en la zona de contacto. Para el contacto entre dos esferas ${\ Displaystyle p_ {0} '}$

${\ displaystyle p_ {0} = {\ frac {2aE ^ {*}} {\ pi R}}; \ quad p_ {0} '= - \ left ({\ frac {4 \ gamma E ^ {*}} {\ pi a}} \ right) ^ {\ frac {1} {2}}}$

donde es el radio del área de contacto, es la fuerza aplicada, es la energía superficial total de ambas superficies por unidad de área de contacto, son los radios, los módulos de Young y las relaciones de Poisson de las dos esferas, y ${\ Displaystyle a \,}$${\ Displaystyle F}$${\ Displaystyle 2 \ gamma}$${\ Displaystyle R_ {i}, \, E_ {i}, \, \ nu _ {i}, ~~ i = 1,2}$

${\ Displaystyle {\ frac {1} {R}} = {\ frac {1} {R_ {1}}} + {\ frac {1} {R_ {2}}}; \ quad {\ frac {1} {E ^ {*}}} = {\ frac {1- \ nu _ {1} ^ {2}} {E_ {1}}} + {\ frac {1- \ nu _ {2} ^ {2} } {E_ {2}}}}$

La distancia de aproximación entre las dos esferas viene dada por

${\ Displaystyle d = {\ frac {\ pi a} {2E ^ {*}}} \ left (p_ {0} + 2p_ {0} '\ right) = {\ frac {a ^ {2}} {R }}}$

La ecuación de Hertz para el área de contacto entre dos esferas, modificada para tener en cuenta la energía superficial, tiene la forma

${\ Displaystyle a ^ {3} = {\ frac {3R} {4E ^ {*}}} \ left (F + 6 \ gamma \ pi R + {\ sqrt {12 \ gamma \ pi RF + (6 \ gamma \ pi R) ^ {2}}} \ derecha)}$

Cuando la energía superficial es cero, se recupera la ecuación de Hertz para el contacto entre dos esferas. Cuando la carga aplicada es cero, el radio de contacto es ${\ Displaystyle \ gamma = 0}$

${\ Displaystyle a ^ {3} = {\ frac {9R ^ {2} \ gamma \ pi} {E ^ {*}}}}$

Se predice que la carga de tracción a la que se separan las esferas (es decir, ) será ${\ Displaystyle a = 0}$

${\ Displaystyle F _ {\ text {c}} = - 3 \ gamma \ pi R \,}$

Esta fuerza también se llama fuerza de arranque . Tenga en cuenta que esta fuerza es independiente de los módulos de las dos esferas. Sin embargo, existe otra posible solución para el valor de con esta carga. Esta es el área de contacto crítica , dada por ${\ Displaystyle a}$${\ Displaystyle a _ {\ text {c}}}$

${\ Displaystyle a _ {\ text {c}} ^ {3} = {\ frac {9R ^ {2} \ gamma \ pi} {4E ^ {*}}}}$

Si definimos el trabajo de adhesión como

${\ Displaystyle \ Delta \ gamma = \ gamma _ {1} + \ gamma _ {2} - \ gamma _ {12}}$

donde están las energías adhesivas de las dos superficies y es un término de interacción, podemos escribir el radio de contacto JKR como ${\ Displaystyle \ gamma _ {1}, \ gamma _ {2}}$${\ Displaystyle \ gamma _ {12}}$

${\ Displaystyle a ^ {3} = {\ frac {3R} {4E ^ {*}}} \ left (F + 3 \ Delta \ gamma \ pi R + {\ sqrt {6 \ Delta \ gamma \ pi RF + (3) \ Delta \ gamma \ pi R) ^ {2}}} \ right)}$

La carga de tracción en la separación es

${\ Displaystyle F = - {\ frac {3} {2}} \ Delta \ gamma \ pi R \,}$

y el radio de contacto crítico viene dado por

${\ Displaystyle a _ {\ text {c}} ^ {3} = {\ frac {9R ^ {2} \ Delta \ gamma \ pi} {8E ^ {*}}}}$

La profundidad crítica de penetración es

${\ Displaystyle d _ {\ text {c}} = {\ frac {a_ {c} ^ {2}} {R}} = \ left (R ^ {\ frac {1} {2}} {\ frac {9 \ Delta \ gamma \ pi} {4E ^ {*}}} \ right) ^ {\ frac {2} {3}}}$

Modelo Derjaguin-Muller-Toporov (DMT) de contacto elástico

El modelo Derjaguin-Muller-Toporov (DMT) es un modelo alternativo para el contacto adhesivo que asume que el perfil de contacto sigue siendo el mismo que en el contacto hertziano pero con interacciones atractivas adicionales fuera del área de contacto.

El radio de contacto entre dos esferas de la teoría DMT es

${\ Displaystyle a ^ {3} = {\ cfrac {3R} {4E ^ {*}}} \ left (F + 4 \ gamma \ pi R \ right)}$

y la fuerza de arranque es

${\ Displaystyle F_ {c} = - 4 \ gamma \ pi R \,}$

Cuando se logra la fuerza de extracción, el área de contacto se vuelve cero y no hay singularidad en las tensiones de contacto en el borde del área de contacto.

En cuanto al trabajo de adhesión ${\ Displaystyle \ Delta \ gamma}$

${\ Displaystyle a ^ {3} = {\ cfrac {3R} {4E ^ {*}}} \ left (F + 2 \ Delta \ gamma \ pi R \ right)}$

y

${\ Displaystyle F_ {c} = - 2 \ Delta \ gamma \ pi R \,}$

Parámetro Tabor

En 1977, Tabor demostró que la aparente contradicción entre las teorías JKR y DMT podía resolverse al señalar que las dos teorías eran los límites extremos de una sola teoría parametrizada por el parámetro de Tabor ( ) definido como ${\ Displaystyle \ mu}$

${\ Displaystyle \ mu: = {\ frac {d_ {c}} {z_ {0}}} \ approx \ left [{\ frac {R (\ Delta \ gamma) ^ {2}} {{E ^ {* }} ^ {2} z_ {0} ^ {3}}} \ right] ^ {\ frac {1} {3}}}$

donde es la separación de equilibrio entre las dos superficies en contacto. La teoría JKR se aplica a esferas grandes y compatibles para las que es grande. La teoría DMT se aplica a esferas pequeñas y rígidas con valores pequeños de . ${\ Displaystyle z_ {0}}$${\ Displaystyle \ mu}$${\ Displaystyle \ mu}$

Posteriormente, Derjaguin y sus colaboradores, al aplicar la ley de fuerza de superficie de Bradley a un semiespacio elástico, confirmaron que a medida que aumenta el parámetro de Tabor, la fuerza de arranque cae del valor de Bradley al valor de JKR . Más tarde, Greenwood realizó cálculos más detallados que revelaron la curva de carga / aproximación en forma de S que explica el efecto de salto. Feng proporcionó un método más eficiente para hacer los cálculos y resultados adicionales. ${\ Displaystyle 2 \ pi R \ Delta \ gamma}$${\ Displaystyle (3/2) \ pi R \ Delta \ gamma}$

Modelo de contacto elástico Maugis-Dugdale

Maugis proporcionó una mejora adicional a la idea de Tabor, quien representó la fuerza de la superficie en términos de una aproximación de la zona cohesiva de Dugdale , de modo que el trabajo de adhesión está dado por

${\ Displaystyle \ Delta \ gamma = \ sigma _ {0} ~ h_ {0}}$

donde es la fuerza máxima predicha por el potencial de Lennard-Jones y es la separación máxima obtenida al hacer coincidir las áreas bajo las curvas de Dugdale y Lennard-Jones (ver figura adyacente). Esto significa que la fuerza de atracción es constante para . No hay mayor penetración en compresión. El contacto perfecto ocurre en un área de radio y las fuerzas adhesivas de magnitud se extienden a un área de radio . En la región , las dos superficies están separadas por una distancia con y . La relación se define como ${\ Displaystyle \ sigma _ {0}}$${\ Displaystyle h_ {0}}$${\ Displaystyle z_ {0} \ leq z \ leq z_ {0} + h_ {0}}$${\ Displaystyle a}$${\ Displaystyle \ sigma _ {0}}$${\ Displaystyle c> a}$${\ Displaystyle a <r <c}$${\ Displaystyle h (r)}$${\ Displaystyle h (a) = 0}$${\ Displaystyle h (c) = h_ {0}}$${\ Displaystyle m}$

${\ Displaystyle m: = {\ frac {c} {a}}}$.

En la teoría de Maugis-Dugdale, la distribución de tracción de la superficie se divide en dos partes: una debido a la presión de contacto de Hertz y la otra a la tensión adhesiva de Dugdale. Se asume el contacto de Hertz en la región . La contribución a la tracción de la superficie de la presión de Hertz viene dada por ${\ Displaystyle -a <r <a}$

${\ Displaystyle p ^ {H} (r) = \ left ({\ frac {3F ^ {H}} {2 \ pi a ^ {2}}} \ right) \ left (1 - {\ frac {r ^ {2}} {a ^ {2}}} \ right) ^ {\ frac {1} {2}}}$

donde la fuerza de contacto de Hertz viene dada por ${\ Displaystyle F ^ {H}}$

${\ Displaystyle F ^ {H} = {\ frac {4E ^ {*} a ^ {3}} {3R}}}$

La penetración debida a la compresión elástica es

${\ Displaystyle d ^ {H} = {\ frac {a ^ {2}} {R}}}$

El desplazamiento vertical en es ${\ Displaystyle r = c}$

${\ Displaystyle u ^ {H} (c) = {\ cfrac {1} {\ pi R}} \ left [a ^ {2} \ left (2-m ^ {2} \ right) \ sin ^ {- 1} \ left ({\ frac {1} {m}} \ right) + a ^ {2} {\ sqrt {m ^ {2} -1}} \ right]}$

y la separación entre las dos superficies en es ${\ Displaystyle r = c}$

${\ Displaystyle h ^ {H} (c) = {\ frac {c ^ {2}} {2R}} - d ^ {H} + u ^ {H} (c)}$

La distribución de tracción de la superficie debido a la tensión adhesiva Dugdale es

${\ Displaystyle p ^ {D} (r) = {\ begin {cases} - {\ frac {\ sigma _ {0}} {\ pi}} \ cos ^ {- 1} \ left [{\ frac {2 -m ^ {2} - {\ frac {r ^ {2}} {a ^ {2}}}} {m ^ {2} \ left (1 - {\ frac {r ^ {2}} {m ^ {2} a ^ {2}}} \ right)}} \ right] & \ quad {\ text {para}} \ quad r \ leq a \\ - \ sigma _ {0} & \ quad {\ text { para}} \ quad a \ leq r \ leq c \ end {cases}}}$

La fuerza adhesiva total viene dada por

${\ Displaystyle F ^ {D} = - 2 \ sigma _ {0} m ^ {2} a ^ {2} \ left [\ cos ^ {- 1} \ left ({\ frac {1} {m}} \ right) + {\ frac {1} {m ^ {2}}} {\ sqrt {m ^ {2} -1}} \ right]}$

La compresión debida a la adhesión de Dugdale es

${\ Displaystyle d ^ {D} = - \ left ({\ frac {2 \ sigma _ {0} a} {E ^ {*}}} \ right) {\ sqrt {m ^ {2} -1}} }$

y la brecha en es ${\ Displaystyle r = c}$

${\ Displaystyle h ^ {D} (c) = \ left ({\ frac {4 \ sigma _ {0} a} {\ pi E ^ {*}}} \ right) \ left [{\ sqrt {m ^ {2} -1}} \ cos ^ {- 1} \ left ({\ frac {1} {m}} \ right) + 1-m \ right]}$

La tracción neta en el área de contacto viene dada por y la fuerza de contacto neta es . Cuando la tracción adhesiva desciende a cero. ${\ Displaystyle p (r) = p ^ {H} (r) + p ^ {D} (r)}$${\ Displaystyle F = F ^ {H} + F ^ {D}}$${\ Displaystyle h (c) = h ^ {H} (c) + h ^ {D} (c) = h_ {0}}$

En esta etapa se introducen valores no dimensionalizados de que se desafían como ${\ Displaystyle a, c, F, d}$

${\ displaystyle {\ bar {a}} = \ alpha a ~; ~~ {\ bar {c}}: = \ alpha c ~; ~~ {\ bar {d}}: = \ alpha ^ {2} Rd ~; ~~ \ alpha: = \ left ({\ frac {4E ^ {*}} {3 \ pi \ Delta \ gamma R ^ {2}}} \ right) ^ {\ frac {1} {3}} ~; ~~ {\ bar {A}}: = \ pi c ^ {2} ~; ~~ {\ bar {F}} = {\ frac {F} {\ pi \ Delta \ gamma R}}}$

Además, Maugis propuso un parámetro que es equivalente al parámetro Tabor . Este parámetro se define como ${\ Displaystyle \ lambda}$${\ Displaystyle \ mu}$

${\ Displaystyle \ lambda: = \ sigma _ {0} \ left ({\ frac {9R} {2 \ pi \ Delta \ gamma {E ^ {*}} ^ {2}}} \ right) ^ {\ frac {1} {3}} \ aproximadamente 1,16 \ mu}$

donde la tensión cohesiva escalonada es igual a la tensión teórica del potencial de Lennard-Jones ${\ Displaystyle \ sigma _ {0}}$

${\ Displaystyle \ sigma _ {\ text {th}} = {\ frac {16 \ Delta \ gamma} {9 {\ sqrt {3}} z_ {0}}}}$

Zheng y Yu sugirieron otro valor para el estrés cohesivo escalonado

${\ Displaystyle \ sigma _ {0} = \ exp \ left (- {\ frac {223} {420}} \ right) \ cdot {\ frac {\ Delta \ gamma} {z_ {0}}} \ approx 0.588 {\ frac {\ Delta \ gamma} {z_ {0}}}}$

para igualar el potencial de Lennard-Jones, lo que conduce a

${\ Displaystyle \ lambda \ approx 0,663 \ mu}$

Entonces la fuerza de contacto neta se puede expresar como

${\ displaystyle {\ bar {F}} = {\ bar {a}} ^ {3} - \ lambda {\ bar {a}} ^ {2} \ left [{\ sqrt {m ^ {2} -1 }} + m ^ {2} \ sec ^ {- 1} m \ right]}$

y la compresión elástica como

${\ Displaystyle {\ bar {d}} = {\ bar {a}} ^ {2} - {\ frac {4} {3}} ~ \ lambda {\ bar {a}} {\ sqrt {m ^ { 2} -1}}}$

La ecuación para el espacio cohesivo entre los dos cuerpos toma la forma

${\ Displaystyle {\ frac {\ lambda {\ bar {a}} ^ {2}} {2}} \ left [\ left (m ^ {2} -2 \ right) \ sec ^ {- 1} m + { \ sqrt {m ^ {2} -1}} \ right] + {\ frac {4 \ lambda {\ bar {a}}} {3}} \ left [{\ sqrt {m ^ {2} -1} } \ sec ^ {- 1} m-m + 1 \ right] = 1}$

Esta ecuación se puede resolver para obtener valores de para varios valores de y . Para valores grandes de , y se obtiene el modelo JKR. Para valores pequeños del modelo DMT se recupera. ${\ Displaystyle c}$${\ Displaystyle a}$${\ Displaystyle \ lambda}$${\ Displaystyle \ lambda}$${\ displaystyle m \ rightarrow 1}$${\ Displaystyle \ lambda}$

Modelo Carpick-Ogletree-Salmeron (COS)

El modelo de Maugis-Dugdale solo se puede resolver iterativamente si el valor de no se conoce a priori. La solución aproximada de Carpick-Ogletree-Salmeron simplifica el proceso al usar la siguiente relación para determinar el radio de contacto : ${\ Displaystyle \ lambda}$${\ Displaystyle a}$

${\ Displaystyle a = a_ {0} (\ beta) \ left ({\ frac {\ beta + {\ sqrt {1-F / F_ ​​{c} (\ beta)}}} {1+ \ beta}} \ derecha) ^ {\ frac {2} {3}}}$

donde es el área de contacto con carga cero, y es un parámetro de transición que se relaciona con por ${\ Displaystyle a_ {0}}$${\ Displaystyle \ beta}$${\ Displaystyle \ lambda}$

${\ Displaystyle \ lambda \ approx -0,924 \ ln (1-1,02 \ beta)}$

El caso corresponde exactamente a la teoría JKR mientras que corresponde a la teoría DMT. Para casos intermedios, el modelo COS se corresponde estrechamente con la solución de Maugis-Dugdale para . ${\ Displaystyle \ beta = 1}$${\ Displaystyle \ beta = 0}$${\ Displaystyle 0 <\ beta <1}$${\ Displaystyle 0.1 <\ lambda <5}$

Influencia de la forma del contacto

Incluso en presencia de superficies perfectamente lisas, la geometría puede entrar en juego en forma de la forma macroscópica de la zona de contacto. Cuando un punzón rígido con la cara plana pero de forma extraña se retira con cuidado de su contraparte blanda, su desprendimiento no ocurre instantáneamente, sino que los frentes de desprendimiento comienzan en las esquinas puntiagudas y viajan hacia adentro, hasta que se alcanza la configuración final que para las formas macroscópicas isotrópicas es casi circular. El principal parámetro que determina la fuerza adhesiva de los contactos planos es el tamaño lineal máximo del contacto. El proceso de desprendimiento puede observarse experimentalmente en la película.

Ver también

Referencias

enlaces externos

• [2] : Se puede encontrar más información sobre las tensiones de contacto y la evolución de las ecuaciones de las tensiones de los cojinetes en esta publicación del director del Centro de Investigación Glenn de la NASA, Erwin Zaretsky, la Sección de Cojinetes, Engranajes y Transmisión de la NASA.
• [3] : Una rutina de MATLAB para resolver el problema de la mecánica de contacto elástico lineal titulado; "Una solución LCP del problema de la mecánica de contacto elástico lineal" se proporciona en el intercambio de archivos en MATLAB Central.
• [4] : Calculadora de mecánica de contactos.
• [5] : cálculos detallados y fórmulas de la teoría JKR para dos esferas.
• [5] : Un código de Matlab para el análisis de contacto de Hertz (incluye casos de líneas, puntos y elípticas).
• [6] : Modelos de adhesión JKR, MD y DMT (rutinas de Matlab).