Gavilla constante - Constant sheaf
En matemáticas , la gavilla constante en un espacio topológico X asociada a un conjunto A es un haz de conjuntos sobre X cuyos tallos son todos iguales a A . Se denota por A o A X . El prehaz constante con el valor A es el prehaz que asigna a cada no vacío subconjunto abierto de X el valor A , y todos cuyos mapas de restricción son el mapa de identidad A → A . La gavilla constante asociada a A es el sheafification de la prehaz constante asociada a A .
En ciertos casos, el conjunto A puede ser reemplazado por un objeto A en alguna categoría C (por ejemplo, cuando C es la categoría de grupos abelianos o anillos conmutativos ).
Las gavillas constantes de grupos abelianos aparecen en particular como coeficientes en la cohomología de gavillas .
Lo esencial
Sea X un espacio topológico y A un conjunto. Las secciones de la gavilla constante A sobre un conjunto abierto U pueden interpretarse como las funciones continuas U → A , donde A recibe la topología discreta . Si U está conectado , entonces estas funciones locales constantes son constantes. Si f : X → {pt} es el único mapa para el espacio de un punto y A se considera como una gavilla en {pt}, entonces la inversa imagen f -1 A es la constante de gavilla A en X . El espacio de la gavilla de A es el mapa de proyección X × A → X (donde A recibe la topología discreta).
Un ejemplo detallado
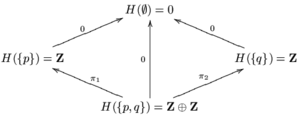
Deje que X sea el espacio topológico que consta de dos puntos p y q con la topología discreta . X tiene cuatro conjuntos abiertos: ∅, { p }, { q }, { p , q }. Las cinco inclusiones no triviales de los conjuntos abiertos de X se muestran en el gráfico.
Una gavilla previa en X elige un conjunto para cada uno de los cuatro conjuntos abiertos de X y un mapa de restricción para cada una de las nueve inclusiones (cinco inclusiones no triviales y cuatro triviales). La gavilla previa constante con valor Z , que denotaremos F , es la gavilla previa que elige los cuatro conjuntos para que sean Z , los enteros y todos los mapas de restricción para que sean la identidad. F es un funtor, por lo tanto, un pregajo, porque es constante. F satisface el axioma de pegado, pero no es una gavilla porque falla el axioma de identidad local en el conjunto vacío. Esto se debe a que el conjunto vacío está cubierto por la familia de conjuntos vacía: al vacío, dos secciones cualesquiera de F sobre el conjunto vacío son iguales cuando se restringen a cualquier conjunto de la familia vacía. Por tanto, el axioma de identidad local implicaría que dos secciones cualesquiera de F sobre el conjunto vacío son iguales, pero esto no es cierto.
Un G anterior de la gavilla similar que satisface el axioma de identidad local sobre el conjunto vacío se construye de la siguiente manera. Sea G (∅) = 0 , donde 0 es un conjunto de un elemento. En todos los conjuntos no vacíos, dar G el valor Z . Para cada inclusión de conjuntos abiertos, G retornos ya sea el único mapa a 0, si el conjunto más pequeño está vacío, o en el mapa de identidad en Z .
Observe que, como consecuencia del axioma de identidad local para el conjunto vacío, todos los mapas de restricción que involucran al conjunto vacío son aburridos. Esto es cierto para cualquier gavilla que satisfaga el axioma de identidad local para el conjunto vacío y, en particular, para cualquier gavilla.
G es una gavilla separada (es decir, satisface el axioma de identidad local), pero a diferencia de F , falla en el axioma de pegado. { p , q } está cubierto por los dos conjuntos abiertos { p } y { q }, y estos conjuntos tienen una intersección vacía. Una sección en { p } o en { q } es un elemento de Z , es decir, es un número. Elija una sección m sobre { p } y n sobre { q }, y suponga que m ≠ n . Debido a que m y n restringe al mismo elemento 0 sobre ∅, el axioma de pegado requiere la existencia de una sección única s en G ({ p , q }) que restringe a m en { p } y n en { q }. Pero debido a que el mapa de restricción de { p , q } a { p } es la identidad, s = m , y de manera similar s = n , entonces m = n , una contradicción.
G ({ p , q }) es demasiado pequeño para transportar información sobre { p } y { q }. Para ampliar de modo que se satisface el axioma encolado, permiten H ({ p , q }) = Z ⊕ Z . Dejar que π 1 y ¸ 2 son los dos mapas de proyección Z ⊕ Z → Z . Definir H ({ p }) = im (π 1 ) = Z y H ({ q }) = im (π 2 ) = Z . Para los conjuntos y las inclusiones abiertas restantes, deja que H es igual a G . H es un fajo llamado la gavilla constante en X con un valor Z . Como Z es un anillo y todos los mapas de restricción son homomorfismos de anillo, H es un haz de anillos conmutativos.
Ver también
Referencias
- Sección II.1 de Hartshorne, Robin (1977), Geometría Algebraica , Textos de Posgrado en Matemáticas , 52 , Nueva York: Springer-Verlag, ISBN 978-0-387-90244-9 , MR 0463157
- Sección 2.4.6 de Tennison, BR (1975), Teoría de la gavilla , ISBN 978-0-521-20784-3