Movimiento circular - Circular motion

Parte de una serie sobre
Mecanica clasica
${\ Displaystyle {\ textbf {F}} = {\ frac {d} {dt}} (m {\ textbf {v}})}$ Segunda ley del movimiento
Historia Cronología Libros de texto
Sucursales
Fundamentos
Formulaciones
Temas centrales
Rotación
Científicos
Portal de física  Categoría
v t mi

En física , el movimiento circular es el movimiento de un objeto a lo largo de la circunferencia de un círculo o la rotación a lo largo de una trayectoria circular. Puede ser uniforme, con una tasa de rotación angular constante y una velocidad constante, o no uniforme con una tasa de rotación cambiante. La rotación alrededor de un eje fijo de un cuerpo tridimensional implica el movimiento circular de sus partes. Las ecuaciones de movimiento describen el movimiento del centro de masa de un cuerpo. En movimiento circular, la distancia entre el cuerpo y un punto fijo en la superficie permanece igual.

Ejemplos de movimiento circular incluyen: un satélite artificial que orbita la Tierra a una altura constante, las aspas de un ventilador de techo que giran alrededor de un eje, una piedra atada a una cuerda y que se balancea en círculos, un automóvil que gira en una curva en una pista de carreras , un electrón que se mueve perpendicularmente a un campo magnético uniforme y un engranaje que gira dentro de un mecanismo.

Dado que el vector de velocidad del objeto cambia constantemente de dirección, el objeto en movimiento experimenta una aceleración por una fuerza centrípeta en la dirección del centro de rotación. Sin esta aceleración, el objeto se movería en línea recta, de acuerdo con las leyes de movimiento de Newton .

Movimiento circular uniforme

Figura 1: Velocidad v y aceleración a en movimiento circular uniforme a una tasa angular ω; la velocidad es constante, pero la velocidad siempre es tangente a la órbita; la aceleración tiene magnitud constante, pero siempre apunta hacia el centro de rotación.

Figura 2: Los vectores de velocidad en el tiempo t y el tiempo t + dt se mueven desde la órbita de la izquierda a nuevas posiciones donde coinciden sus colas, a la derecha. Debido a que la velocidad tiene una magnitud fija en v = r ω, los vectores de velocidad también barren una trayectoria circular a una tasa angular ω. Cuando dt → 0, el vector de aceleración a se vuelve perpendicular av , lo que significa que apunta hacia el centro de la órbita en el círculo de la izquierda. El ángulo ω dt es el ángulo muy pequeño entre las dos velocidades y tiende a cero cuando dt → 0.

Figura 3: (Izquierda) Bola en movimiento circular: la cuerda proporciona fuerza centrípeta para mantener la bola en círculo (Derecha) Se corta la cuerda y la bola continúa en línea recta con la velocidad en el momento de cortar la cuerda, de acuerdo con la ley de inercia de Newton. porque la fuerza centrípeta ya no existe.

En física , el movimiento circular uniforme describe el movimiento de un cuerpo que atraviesa una trayectoria circular a velocidad constante . Dado que el cuerpo describe un movimiento circular, su distancia desde el eje de rotación permanece constante en todo momento. Aunque la velocidad del cuerpo es constante, su velocidad no es constante: la velocidad, una cantidad vectorial , depende tanto de la velocidad del cuerpo como de su dirección de viaje. Esta velocidad cambiante indica la presencia de una aceleración; esta aceleración centrípeta es de magnitud constante y está dirigida en todo momento hacia el eje de rotación. Esta aceleración es, a su vez, producida por una fuerza centrípeta también constante en magnitud y dirigida hacia el eje de rotación.

En el caso de la rotación alrededor de un eje fijo de un cuerpo rígido que no es despreciable en comparación con el radio de la trayectoria, cada partícula del cuerpo describe un movimiento circular uniforme con la misma velocidad angular, pero con velocidad y aceleración que varían con la posición con respecto al eje.

Fórmulas

Figura 1: Relaciones vectoriales para movimiento circular uniforme; El vector ω que representa la rotación es normal al plano de la órbita.

Para el movimiento en un círculo de radio r , la circunferencia del círculo es C = 2 π r . Si el período para una rotación es T , la tasa angular de rotación, también conocida como velocidad angular , ω es:

${\ Displaystyle \ omega = {\ frac {2 \ pi} {T}} = 2 \ pi f = {\ frac {d \ theta} {dt}}}$ y las unidades son radianes / segundo

La velocidad del objeto que recorre el círculo es:

${\ Displaystyle v = {\ frac {2 \ pi r} {T}} = \ omega r}$

El ángulo θ barrido en un tiempo t es:

${\ Displaystyle \ theta = 2 \ pi {\ frac {t} {T}} = \ omega t \,}$

La aceleración angular , α , de la partícula es:

${\ Displaystyle \ alpha = {\ frac {d \ omega} {dt}}}$

En el caso de un movimiento circular uniforme, α será cero.

La aceleración debida al cambio de dirección es:

${\ Displaystyle a_ {c} = {\ frac {v ^ {2}} {r}} = \ omega ^ {2} r}$

La fuerza centrípeta y centrífuga también se puede averiguar mediante la aceleración:

${\ Displaystyle F_ {c} = {\ dot {p}} \ {\ overset {{\ dot {m}} = 0} {=}} \ ma_ {c} = {\ frac {mv ^ {2}} {r}}}$

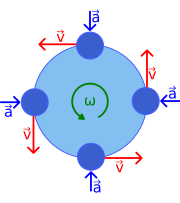
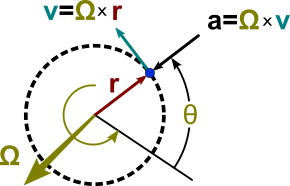
Las relaciones vectoriales se muestran en la Figura 1. El eje de rotación se muestra como un vector ω perpendicular al plano de la órbita y con una magnitud ω = d θ / dt . La dirección de ω se elige usando la regla de la mano derecha . Con esta convención para representar la rotación, la velocidad viene dada por un producto vectorial cruzado como

${\ Displaystyle \ mathbf {v} = {\ boldsymbol {\ omega}} \ times \ mathbf {r},}$

que es un vector perpendicular tanto a ω como a r ( t ), tangencial a la órbita y de magnitud ω r . Asimismo, la aceleración viene dada por

${\ Displaystyle \ mathbf {a} = {\ boldsymbol {\ omega}} \ times \ mathbf {v} = {\ boldsymbol {\ omega}} \ times \ left ({\ boldsymbol {\ omega}} \ times \ mathbf {r} \ derecha),}$

que es un vector perpendicular tanto a ω como a v ( t ) de magnitud ω | v | = ω ² r y dirigido exactamente opuesto a r ( t ).

En el caso más simple, la velocidad, la masa y el radio son constantes.

Considere un cuerpo de un kilogramo, que se mueve en un círculo de un metro de radio , con una velocidad angular de un radián por segundo .

• La velocidad es de 1 metro por segundo.
• La aceleración hacia adentro es de 1 metro por segundo cuadrado, v ² / r.
• Está sujeto a una fuerza centrípeta de 1 kilogramo de metro por segundo cuadrado, que es un newton .
• La cantidad de movimiento del cuerpo es 1 kg · m · s ⁻¹ .
• El momento de inercia es 1 kg · m ² .
• El momento angular es 1 kg · m ² · s ⁻¹ .
• La energía cinética es de 1 julio .
• La circunferencia de la órbita es de 2 π (~ 6.283) metros.
• El período del movimiento es de 2 π segundos por turno .
• La frecuencia es (2 π ) ⁻¹ hertz .

En coordenadas polares

Figura 4: Coordenadas polares para trayectoria circular. A la izquierda hay un círculo unitario que muestra los cambios y en los vectores unitarios y para un pequeño incremento en el ángulo .${\ Displaystyle \ mathbf {d {\ hat {u}} _ {R}}}$${\ Displaystyle \ mathbf {d {\ hat {u}} _ {\ theta}}}$${\ Displaystyle \ mathbf {{\ hat {u}} _ {R}}}$${\ Displaystyle \ mathbf {{\ hat {u}} _ {\ theta}}}$${\ Displaystyle \ mathrm {d \ theta}}$${\ Displaystyle \ mathrm {\ theta}}$

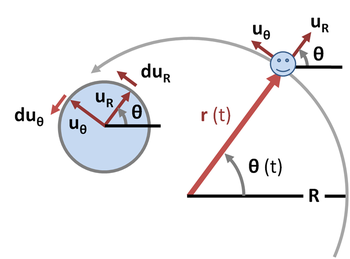
Durante el movimiento circular, el cuerpo se mueve en una curva que se puede describir en el sistema de coordenadas polares como una distancia fija R desde el centro de la órbita tomada como origen, orientada en un ángulo θ ( t ) desde alguna dirección de referencia. Consulte la Figura 4. El vector de desplazamiento es el vector radial desde el origen hasta la ubicación de la partícula: ${\ Displaystyle {\ vec {r}}}$

${\ Displaystyle {\ vec {r}} (t) = R {\ hat {u}} _ {R} (t) \,}$

donde es el vector unitario paralelo al vector de radio en el tiempo t y apuntando en dirección opuesta al origen. Es conveniente introducir también el vector unitario ortogonal a , a saber . Se acostumbra orientar para señalar en la dirección de viaje a lo largo de la órbita. ${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$

La velocidad es la derivada del desplazamiento en el tiempo:

${\ Displaystyle {\ vec {v}} (t) = {\ frac {d} {dt}} {\ vec {r}} (t) = {\ frac {dR} {dt}} {\ hat {u }} _ {R} (t) + R {\ frac {d {\ hat {u}} _ {R}} {dt}} \.}$

Debido a que el radio del círculo es constante, la componente radial de la velocidad es cero. El vector unitario tiene una magnitud invariante en el tiempo de la unidad, por lo que a medida que el tiempo varía, su punta siempre se encuentra en un círculo de radio unitario, con un ángulo θ igual que el ángulo de . Si el desplazamiento de la partícula gira en un ángulo d θ en el tiempo dt , también lo hace , describiendo un arco en el círculo unitario de magnitud d θ. Vea el círculo unitario a la izquierda de la Figura 4. Por lo tanto: ${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ vec {r}} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$

${\ Displaystyle {\ frac {d {\ hat {u}} _ {R}} {dt}} = {\ frac {d \ theta} {dt}} {\ hat {u}} _ {\ theta} ( t) \,}$

donde la dirección del cambio debe ser perpendicular a (o, en otras palabras, a lo largo ) porque cualquier cambio en la dirección de cambiaría el tamaño de . El signo es positivo, porque un aumento de d θ implica el objeto y se ha movido en la dirección de . Por lo tanto, la velocidad se convierte en: ${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$${\ Displaystyle d {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$

${\ Displaystyle {\ vec {v}} (t) = {\ frac {d} {dt}} {\ vec {r}} (t) = R {\ frac {d {\ hat {u}} _ { R}} {dt}} = R {\ frac {d \ theta} {dt}} {\ hat {u}} _ {\ theta} (t) = R \ omega {\ hat {u}} _ {\ theta} (t) \.}$

La aceleración del cuerpo también se puede dividir en componentes radiales y tangenciales. La aceleración es la derivada del tiempo de la velocidad:

${\ Displaystyle {\ begin {alineado} {\ vec {a}} (t) & = {\ frac {d} {dt}} {\ vec {v}} (t) = {\ frac {d} {dt }} \ left (R \ omega {\ hat {u}} _ {\ theta} (t) \ right) \\ & = R \ left ({\ frac {d \ omega} {dt}} {\ hat { u}} _ {\ theta} (t) + \ omega {\ frac {d {\ hat {u}} _ {\ theta}} {dt}} \ right) \. \ end {alineado}}}$

La derivada de tiempo de se encuentra de la misma forma que para . Nuevamente, es un vector unitario y su punta traza un círculo unitario con un ángulo que es π / 2 + θ. Por lo tanto, un aumento en el ángulo d θ por implica traza un arco de magnitud d θ, y como es ortogonal a , tenemos: ${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$${\ Displaystyle {\ vec {r}} (t)}$${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$

${\ Displaystyle {\ frac {d {\ hat {u}} _ {\ theta}} {dt}} = - {\ frac {d \ theta} {dt}} {\ hat {u}} _ {R} (t) = - \ omega {\ hat {u}} _ {R} (t) \,}$

donde es necesario mantener un signo negativo ortogonal . (De lo contrario, el ángulo entre y sería disminuir con el aumento en d . Θ) Ver el círculo unidad a la izquierda de la figura 4. Por consiguiente, la aceleración es: ${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$${\ Displaystyle {\ hat {u}} _ {\ theta} (t)}$${\ Displaystyle {\ hat {u}} _ {R} (t)}$

${\ Displaystyle {\ begin {alineado} {\ vec {a}} (t) & = R \ left ({\ frac {d \ omega} {dt}} {\ hat {u}} _ {\ theta} ( t) + \ omega {\ frac {d {\ hat {u}} _ {\ theta}} {dt}} \ right) \\ & = R {\ frac {d \ omega} {dt}} {\ hat {u}} _ {\ theta} (t) - \ omega ^ {2} R {\ hat {u}} _ {R} (t) \. \ end {alineado}}}$

La aceleración centrípeta es el componente radial, que se dirige radialmente hacia adentro:

${\ Displaystyle {\ vec {a}} _ {R} (t) = - \ omega ^ {2} R {\ hat {u}} _ {R} (t) \,}$

mientras que la componente tangencial cambia la magnitud de la velocidad:

${\ Displaystyle {\ vec {a}} _ {\ theta} (t) = R {\ frac {d \ omega} {dt}} {\ hat {u}} _ {\ theta} (t) = {\ frac {dR \ omega} {dt}} {\ hat {u}} _ {\ theta} (t) = {\ frac {d \ left | {\ vec {v}} (t) \ right |} {dt }} {\ hat {u}} _ {\ theta} (t) \.}$

Usando números complejos

El movimiento circular se puede describir utilizando números complejos . Sea el eje x el eje real y el eje el eje imaginario. La posición del cuerpo se puede dar como un "vector" complejo: ${\ Displaystyle y}$${\ Displaystyle z}$

${\ Displaystyle z = x + iy = R (\ cos [\ theta (t)] + i \ sin [\ theta (t)]) = Re ^ {i \ theta (t)} \,}$

donde i es la unidad imaginaria , y es el argumento del número complejo en función del tiempo, t . ${\ Displaystyle \ theta (t)}$

Dado que el radio es constante:

${\ Displaystyle {\ dot {R}} = {\ ddot {R}} = 0 \,}$

donde un punto indica diferenciación con respecto al tiempo.

Con esta notación la velocidad se convierte en:

${\ Displaystyle v = {\ dot {z}} = {\ frac {d \ left (Re ^ {i \ theta [t]} \ right)} {dt}} = R {\ frac {d \ left (e ^ {i \ theta [t]} \ right)} {dt}} = Re ^ {i \ theta (t)} {\ frac {d (i \ theta [t])} {dt}} = iR {\ punto {\ theta}} (t) e ^ {i \ theta (t)} = i \ omega Re ^ {i \ theta (t)} = i \ omega z}$

y la aceleración se convierte en:

${\ Displaystyle {\ begin {alineado} a & = {\ dot {v}} = i {\ dot {\ omega}} z + i \ omega {\ dot {z}} = \ left (i {\ dot {\ omega}} - \ omega ^ {2} \ right) z \\ & = \ left (i {\ dot {\ omega}} - \ omega ^ {2} \ right) Re ^ {i \ theta (t)} \\ & = - \ omega ^ {2} Re ^ {i \ theta (t)} + {\ dot {\ omega}} e ^ {i {\ frac {\ pi} {2}}} Re ^ {i \ theta (t)} \. \ end {alineado}}}$

El primer término es opuesto en dirección al vector de desplazamiento y el segundo es perpendicular a él, al igual que los resultados anteriores mostrados anteriormente.

Velocidad

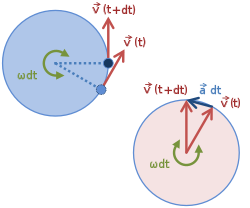
La Figura 1 ilustra los vectores de velocidad y aceleración para un movimiento uniforme en cuatro puntos diferentes de la órbita. Debido a que la velocidad v es tangente a la trayectoria circular, no hay dos velocidades que apunten en la misma dirección. Aunque el objeto tiene una velocidad constante , su dirección siempre cambia. Este cambio de velocidad es causado por una aceleración a , cuya magnitud (como la de la velocidad) se mantiene constante, pero cuya dirección también cambia siempre. La aceleración apunta radialmente hacia adentro ( centrípeto ) y es perpendicular a la velocidad. Esta aceleración se conoce como aceleración centrípeta.

Para una trayectoria de radio r , cuando se barre un ángulo θ, la distancia recorrida en la periferia de la órbita es s = r θ. Por lo tanto, la velocidad de viaje alrededor de la órbita es

${\ Displaystyle v = r {\ frac {d \ theta} {dt}} = r \ omega,}$

donde la velocidad angular de rotación es ω. (Por reordenamiento, ω = v / r .) Por lo tanto, v es una constante, y el vector de velocidad v también rota con magnitud constante v , a la misma tasa angular ω.

Movimiento circular relativista

En este caso, el vector de tres aceleraciones es perpendicular al vector de tres velocidades,

${\ Displaystyle {\ vec {u}} \ cdot {\ vec {a}} = 0.}$

y el cuadrado de la aceleración adecuada, expresado como un invariante escalar, el mismo en todos los marcos de referencia,

${\ Displaystyle \ alpha ^ {2} = \ gamma ^ {4} a ^ {2} + \ gamma ^ {6} ({\ vec {u}} \ cdot {\ vec {a}}) ^ {2} ,}$

se convierte en la expresión del movimiento circular,

${\ Displaystyle \ alpha ^ {2} = \ gamma ^ {4} a ^ {2}.}$

o, tomando la raíz cuadrada positiva y usando la aceleración de tres, llegamos a la aceleración adecuada para el movimiento circular:

${\ Displaystyle \ alpha = \ gamma ^ {2} {\ frac {v ^ {2}} {r}}.}$

Aceleración

El círculo de la izquierda en la Figura 2 es la órbita que muestra los vectores de velocidad en dos momentos adyacentes. A la derecha, estas dos velocidades se mueven para que coincidan sus colas. Como la velocidad es constante, los vectores de velocidad de la derecha trazan un círculo a medida que avanza el tiempo. Para un ángulo de barrido d θ = ω dt el cambio en v es un vector en ángulos rectos av y de magnitud v d θ, lo que a su vez significa que la magnitud de la aceleración está dada por

${\ Displaystyle a_ {c} = v {\ frac {d \ theta} {dt}} = v \ omega = {\ frac {v ^ {2}} {r}}}$

No uniforme

En un movimiento circular no uniforme, un objeto se mueve en una trayectoria circular con una velocidad variable . Dado que la velocidad está cambiando, hay una aceleración tangencial además de la aceleración normal.

En el movimiento circular no uniforme, la aceleración neta (a) es a lo largo de la dirección de Δv, que se dirige dentro del círculo pero no pasa por su centro (ver figura). La aceleración neta se puede descomponer en dos componentes: aceleración tangencial y aceleración normal, también conocida como aceleración centrípeta o radial. A diferencia de la aceleración tangencial, la aceleración centrípeta está presente tanto en el movimiento circular uniforme como en el no uniforme.

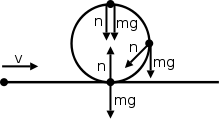
En el movimiento circular no uniforme, la fuerza normal no siempre apunta en la dirección opuesta al peso . Aquí hay un ejemplo con un objeto que viaja en una ruta recta y luego vuelve a dar un bucle en una ruta recta nuevamente.

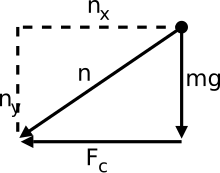
Este diagrama muestra la fuerza normal apuntando en otras direcciones en lugar de oponerse a la fuerza del peso. La fuerza normal es en realidad la suma de las fuerzas radial y tangencial. El componente de la fuerza del peso es responsable de la fuerza tangencial aquí (hemos despreciado la fuerza de fricción). La fuerza radial (fuerza centrípeta) se debe al cambio en la dirección de la velocidad como se discutió anteriormente.

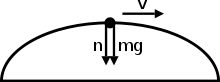
En un movimiento circular no uniforme, la fuerza y ​​el peso normales pueden apuntar en la misma dirección. Ambas fuerzas pueden apuntar hacia abajo, pero el objeto permanecerá en una trayectoria circular sin caer directamente hacia abajo. Primero veamos por qué la fuerza normal puede apuntar hacia abajo en primer lugar. En el primer diagrama, digamos que el objeto es una persona sentada dentro de un avión, las dos fuerzas apuntan hacia abajo solo cuando llega a la parte superior del círculo. La razón de esto es que la fuerza normal es la suma de la fuerza tangencial y la fuerza centrípeta. La fuerza tangencial es cero en la parte superior (ya que no se realiza ningún trabajo cuando el movimiento es perpendicular a la dirección de la fuerza aplicada. Aquí la fuerza del peso es perpendicular a la dirección del movimiento del objeto en la parte superior del círculo) y puntos de fuerza centrípeta hacia abajo, por lo que la fuerza normal también apuntará hacia abajo. Desde un punto de vista lógico, una persona que viaja en el avión estará boca abajo en la parte superior del círculo. En ese momento, el asiento de la persona está empujando hacia abajo a la persona, que es la fuerza normal.

La razón por la que el objeto no cae cuando se somete solo a fuerzas descendentes es simple. Piense en lo que mantiene levantado un objeto después de que se lanza. Una vez que un objeto se lanza al aire, solo existe la fuerza descendente de la gravedad terrestre que actúa sobre el objeto. Eso no significa que una vez que un objeto se lanza al aire, caerá instantáneamente. Lo que mantiene ese objeto en el aire es su velocidad . La primera de las leyes del movimiento de Newton establece que la inercia de un objeto lo mantiene en movimiento y, dado que el objeto en el aire tiene una velocidad, tenderá a seguir moviéndose en esa dirección.

También se puede lograr una velocidad angular variable para un objeto que se mueve en una trayectoria circular si el cuerpo giratorio no tiene una distribución de masa homogénea. Para objetos no homogéneos, es necesario abordar el problema como en.

Aplicaciones

La resolución de aplicaciones que se ocupan de movimientos circulares no uniformes implica el análisis de fuerzas. Con un movimiento circular uniforme, la única fuerza que actúa sobre un objeto que viaja en un círculo es la fuerza centrípeta. En el movimiento circular no uniforme, hay fuerzas adicionales que actúan sobre el objeto debido a una aceleración tangencial distinta de cero. Aunque hay fuerzas adicionales que actúan sobre el objeto, la suma de todas las fuerzas que actúan sobre el objeto tendrá que ser igual a la fuerza centrípeta.

${\ Displaystyle {\ begin {alineado} F _ {\ text {net}} & = ma \\ F _ {\ text {net}} & = ma_ {r} \\ F _ {\ text {net}} & = {\ frac {mv ^ {2}} {r}} \\ F _ {\ text {net}} & = F_ {c} \ end {alineado}}}$

La aceleración radial se utiliza para calcular la fuerza total. La aceleración tangencial no se usa para calcular la fuerza total porque no es responsable de mantener el objeto en una trayectoria circular. La única aceleración responsable de mantener un objeto en movimiento en un círculo es la aceleración radial. Dado que la suma de todas las fuerzas es la fuerza centrípeta, no es necesario dibujar la fuerza centrípeta en un diagrama de cuerpo libre y, por lo general, no se recomienda.

Usando , podemos dibujar diagramas de cuerpo libre para enumerar todas las fuerzas que actúan sobre un objeto y luego igualarlo a . Posteriormente, podemos resolver lo que se desconoce (esto puede ser masa, velocidad, radio de curvatura, coeficiente de fricción, fuerza normal, etc.). Por ejemplo, la imagen anterior que muestra un objeto en la parte superior de un semicírculo se expresaría como . ${\ Displaystyle F _ {\ text {net}} = F_ {c}}$${\ Displaystyle F_ {c}}$${\ Displaystyle F_ {c} = n + mg}$

En movimiento circular uniforme, la aceleración total de un objeto en una trayectoria circular es igual a la aceleración radial. Debido a la presencia de aceleración tangencial en un movimiento circular no uniforme, eso ya no es cierto. Para encontrar la aceleración total de un objeto en circular no uniforme, encuentre la suma vectorial de la aceleración tangencial y la aceleración radial.

${\ Displaystyle {\ sqrt {a_ {r} ^ {2} + a_ {t} ^ {2}}} = a}$

La aceleración radial sigue siendo igual a . Aceleración tangencial es simplemente la derivada de la velocidad en cualquier punto dado: . Esta suma raíz de cuadrados de aceleraciones radiales y tangenciales separadas solo es correcta para el movimiento circular; para el movimiento general dentro de un plano con coordenadas polares , se debe agregar el término de Coriolis , mientras que la aceleración radial se convierte en . ${\ Displaystyle {\ frac {v ^ {2}} {r}}}$${\ Displaystyle a_ {t} = {\ frac {dv} {dt}}}$${\ Displaystyle (r, \ theta)}$${\ Displaystyle a_ {c} = 2 \ left ({\ frac {dr} {dt}} \ right) \ left ({\ frac {d \ theta} {dt}} \ right)}$${\ Displaystyle a_ {t}}$${\ Displaystyle a_ {r} = {\ frac {-v ^ {2}} {r}} + {\ frac {d ^ {2} r} {dt ^ {2}}}}$

Ver también

• Momento angular
• Ecuaciones de movimiento para movimiento circular
• Ejemplo: movimiento circular
• Fuerza ficticia
• Órbita geoestacionaria
• Órbita geosincrónica
• Péndulo (matemáticas)
• Fuerza centrífuga reactiva
• Movimiento recíproco
• Movimiento armónico simple # Movimiento circular uniforme
• Honda (arma)

Referencias

enlaces externos

• Physclips: Mecánica con animaciones y videoclips de la Universidad de Nueva Gales del Sur
• Movimiento circular : un capítulo de un libro de texto en línea
• Conferencia de movimiento circular : una conferencia en video sobre CM
• [1] - un libro de texto en línea con diferentes análisis para el movimiento circular